Zadanie
Záhradník Adam sa jedného dňa zobudil a zistil, že zdedil obrovské pole. Pole to nebolo len také, bolo to pole iné, bolo to pole veľké, priam rozsiahle a na Adamove prekvapenie nebolo uložené v počítači, ale jednalo sa o poriadne pole, s traktormi, hnojiskami a zavlažovačmi.
Tak sa Adam rozhodol že bude teda poriadne záhradníčiť.
Prvý krok je inšpekcia pôdy.
Na poli je \(n\) zavlažovačov, ktoré sú vskutku atypické – každý zavlažovač je natočený do jedného zo štyroch smerov (doprava dole, doprava hore, doľava dole alebo doľava hore) a rovnomerne zavlažuje všetku plochu v rohu na ktorý je natočený. Rôzne zavlažovače zavlažujú s rôznou intenzitou. Zavlažovače sú fixne zabudované v poli a Adam s nimi nevie hýbať.
Adam má \(m\) miest na poli, kde by chcel začať pestovať. Avšak najskôr by potreboval vedieť, ako veľmi zavlažované jednotlivé miesta sú. Pomôžte mu!
Úloha
Na poli je \(n\leq 100\,000\) zavlažovačov, a \(m\leq 20\,000\) miest ktoré Adama zaujímajú.
Každý zavlažovač má danú pozíciu na poli, smer a intenzitu. Zavlažovač zavlažuje tú čast poľa na ktorú je nasmerovaný. Ak je napríklad zavlažovač na pozícii (0,0) a je nastavený doprava-hore, zavlažuje všetky políčka s nezápornými súradnicami.
Vlaha na pozícii je súčet intenzít všetkých zavlažovačov zavlažujúcich túto časť poľa.
Pre všetky miesta, ktoré Adama zaujímajú zistite, aká je ich vlaha.
Navyše, v niektorých sadách by chcel Adam vedieť odpovede ihneď - predtým ako sa spýta ďalšiu otázku. Na získanie plného počtu bodov musí váš program vedieť odpovedať online.
Formát vstupu
Na prvom riadku vstupu sa nachádza číslo \(n\) (\(1 \leq n \leq 100\,000\)).
Na ďalších \(n\) riadkoch sú medzerou oddelené čísla \(x_i\), \(y_i\) – pozície \(i\)-teho zavlažovača, \(v_i\) – intenzita \(i\)-teho zavlažovača a ukazovateľ smeru. “DP” znamená dole-pravo, \(DL\) je dole-ľavo, \(HL\) je hore-ľavo a \(HP\) je hore-pravo.
Nasledujú dve medzerou oddelené celé čísla \(m\) (\(1\leq m\leq 20\,000\)) – počet miest, ktoré zaujímajú Adama, a \(k\) (\(0\leq k\leq 1\)).
Nasleduje \(m\) riadkov, na každom z nich sú dve medzerou oddelené čísla, \(x\) \(y\). Ak \(k = 0\), potom pozície miesta sú \(x\) \(y\).
Ak \(k = 1\), nech \(a\) je vlhkosť predchádzajúceho miesta. Potom súradnice sú \(x \oplus a\) \(y\oplus a\), kde \(\oplus\) je bitový xor.
Pozície miest a zavlažovačov sa môžu zhodovať. Dva zavlažovače sa môžu nachádzať na rovnakom mieste.
Všetky súradnice v absolútnej hodnote nepresahujú \(10^9\). Všetky intenzity sú celé čísla v rozsahu \(1\) až \(10^4\).
Formát výstupu
Vypíšte \(m\) riadkov, na každom z nich vlahu na \(i\)-tom mieste, v poradí v akom boli zadané na vstupe.
Hodnotenie
Existuje \(8\) testovacích sád, každá za jeden bod.
V prvých dvoch sadách sú všetky súradnice medzi \(0\) a \(1000\).
V prvej a tretej sade platí, že \(m, n \leq 1000\).
V štvrtej a piatej sade navyše platí, že všetky súradnice sú medzi \(0\) a \(10^5\).
Vo všetkých sadách okrem siedmej a ôsmej platí \(k = 0\).
Príklady
Input:
5
-1 -1 1 DL
-1 1 2 HL
1 -1 4 DP
1 1 8 HP
0 1 3 DP
7 0
-100 100
0 1
2 1
-1 0
0 -5
2 -2
-1000000000 -1000000000Output:
2
3
11
0
3
7
1Input:
5
-1 -1 1 DL
-1 1 2 HL
1 -1 4 DP
1 1 8 HP
0 1 3 DP
2 1
-100 100
2 3Output:
2
3*Pozície zavlažovačov a miest sú rovnaké ako v prvom vstupe. Lenže v tomto prípade je \(k = 1\).
Hrubá sila
Keby mal Adam veľa času a trpezlivosti, mohol by na riešenie ísť hrubou silou: vždy, keď ho začne zaujímať nejaké miesto, pre každý zavlažovač samostatne skontroluje či miesto zavlažuje. To vie zistiť v konštantom čase.
Takto vie zistiť vlahu všetkých miest v \(O(nm)\) čase a \(O(n)\) pamäti.
Žiaľ, hrubá sila stačí len na prvú a tretiu sadu.
Malé pole
Čo ak je Adamove pole malé? Potom by si Adam mohol spočítať odpoveď pre každé miesto na poli, a potom vie odpovedať na otázku o akomkoľvek mieste, ktoré by ho mohlo zaujímať.
Ako to vie spočítať? Mohol by napríklad použiť 2D prefixové súčty. Viac o tom, ako ich viete použiť sa už dozviete v KSP kuchárke.
Presnejšie, Adam si chce spraviť prefixové súčty pre každý zo štyroch smerov, a vlahu na mieste záujmu potom dostane ako sumu vláh zo všetkých smerov. Toto vie Adam spočítať v časovej zložitosti \(O(m + n + (\max(x_i, y_i))^2)\), a v pamäti \(O((\max(x_i, y_i))^2)\).
K rýchlemu riešeniu
Hrubá sila očividne nestačí. Skúsme sa najskôr zamyslieť nad prípadom, že všetky zavlažovače sú orientované rovnako. Pozrime sa na miesto ktoré Adama momentálne zaujíma. Ktoré zavlažovače ho zasahujú?
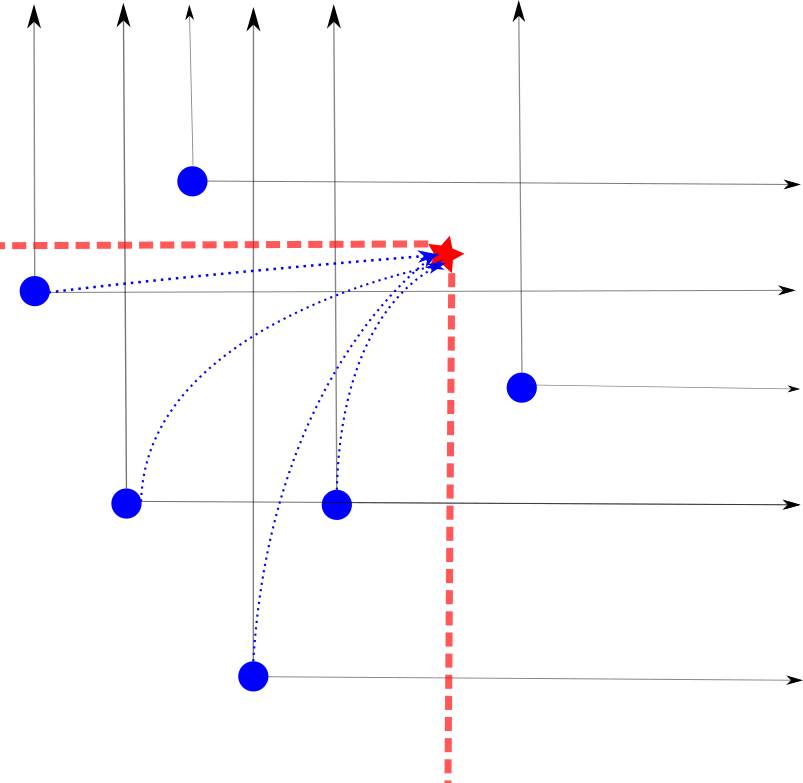
Ako môžme vidieť na ilustračnom obrázku, vyznačené miesto (červeným) zavlažujú všetky zavlažovače v červenom rohu, takže aby sme rýchlo zistili vlahu, chceli by sme vedieť zistiť rýchlo spočítať sumu vláh zavlažovačov umiestnených v danom rohu. Skúsenejšiemu riešiteľovi už možno niečo hovorí, že by sa Adamovi zišiel intervalový strom.
Vieme miesta vopred
Na prvý pohľad by to mohlo vyzerať, že bude treba dvojrozmerný intervalový strom, ale ukáže sa, že ten vôbec netreba. Najskôr sa pozrime na prípad, že Adam vie, ktoré miesta ho zaujímajú vopred.
Zoberme si prípad, že všetky zavlažovače smerujú hore a doprava (ako na obrázku hore). Utrieďme si ich v smere x-súradnice (zľava doprava), a utrieďme si tiež všetky miesta v smere x-súradníc. Potom postupne prechádzajme miesta a zavlažovače zľava doprava a udržujme si dátovú štruktúru, ktorá nám bude hovoriť, pre každú y-súradnicu, koľko je suma vláh zo všetkých zavlažovačov, ktoré sme videli doteraz, na tejto súradnici. Všimnime si (ak sú všetky orientované hore a doprava), že pokiaľ máme spracované všetky zavlažovače naľavo alebo s rovnakou x-súradnicou ako miesto, ktoré nás zaujíma, tak potom vlaha na mieste záujmu je suma vláh všetkých spracovaných zavlažovačov s y-pozíciou menšou alebo rovnou ako miesto záujmu.
Takže nám na efektívne riešenie stačí vedieť spočítať a aktualizovať sumy na intervaloch. To ide napríklad intervalovým stromom.
Veľmi veľké pole
Ak by sme si chceli v intervalovom strome pamätať vlahy na všetkých y-súradniciach, potom nám riešenie zaberie \(O((n+m)\log\max_i y_i + \max_i y_i)\) času a \(O(n + m + \max_i y_i)\) pamäte. Pre pole veľkosti \(10^9\) nám to nestačí.
Ako to zlepšiť? Všimnime si, že nás zaujíma iba relatívna pozícia zavlažovačov a miest, a tých je málo. Teda si zmeňme súradnicovú sústavu pomocou kompresie súradníc. To znamená, utrieďme si všetky x a y súradnice na vstupe, a potom zmenňme súradnice vstupu tak, že najmenšia x-súradnica sa zmení na 0, druhá najmenšia na 1, atď. Takto sa nám zmenší počet y-súradníc ktoré nás zaujímajú na dostatočne málo a dostaneme (offline) riešenie v čase \(O((n+m)\log n)\) a pamäti \(O(m+n)\).
Online riešenie
Čo ak nám miesta prichádzajú postupne?
Nevieme použiť predchádzajúce riešenie: miesta nám neprichádzajú utriedene, potrebovali by sme sa vedieť “dostať” ku intervalovému stromu v rôznych časoch, napríklad “po pridaní všetkých zavlažovačov s x-súradnicou menšou než \(5462\)”.
Alebo by sme to mohli urobiť? Ukazuje sa že áno, riešením je perzistentný intervalový strom. Vysvetlenie ako na perzistentný intervaláč vám nechávam napríklad v tomto videovzoráku.
Riešenie pomocou perzistentného intervaláča funguje v čase \(O((m+n)\log n)\) a v pamäti \(O(n\log n)\) a dá vám plný počet bodov.
Čo s inými smermi?
Pozorný čitateľ ešte zbystrí: hovorím, že už máme riešenie, ale starali sme sa zatiaľ len o jeden smer? Veď zavlažovače vedia byť aj inak orientované!
Ukáže sa, že nám stačí roztriediť si zavlažovače do skupín podľa smeru zavlažovania, a pre každý mať separátny intervaláč. Riešenie vieme použiť pre každý smer rovnaké, len si je treba situáciu vhodne rotovať. Toto nám pridá do časovej a pamäťovej zložitosti iba konštantný faktor.
#include<bits/stdc++.h>
using namespace std;
#define FOR(i,n) for(int i=0;i<(int)n;i++)
#define FOB(i,n) for(int i=n;i>=1;i--)
#define MP(x,y) make_pair((x),(y))
#define ii pair<int, int>
#define lli long long int
#define ld long double
#define ulli unsigned long long int
#define lili pair<lli, lli>
#ifdef EBUG
#define DBG if(1)
#else
#define DBG if(0)
#endif
#define SIZE(x) int(x.size())
const int infinity = 2000000999;
const long long int inff = 4000000000000000999;
typedef complex<long double> point;
template<class T>
T get() {
T a;
cin >> a;
return a;
}
template <class T, class U>
ostream& operator<<(ostream& out, const pair<T, U> &par) {
out << "[" << par.first << ";" << par.second << "]";
return out;
}
template <class T>
ostream& operator<<(ostream& out, const set<T> &cont) {
out << "{";
for (const auto &x:cont) out << x << ", ";
out << "}";
return out;
}
template <class T, class U>
ostream& operator<<(ostream& out, const map<T,U> &cont) {
out << "{";
for (const auto &x:cont) out << x << ", ";
out << "}"; return out;
}
template <class T>
ostream& operator<<(ostream& out, const vector<T>& v) {
FOR(i, v.size()){
if(i) out << " ";
out << v[i];
}
out << endl;
return out;
}
bool ccw(point p, point a, point b) {
if((conj(a - p) * (b - p)).imag() <= 0) return false;
else return true;
}
struct zavlahovac {
int x, y;
int vlaha;
string dir;
const bool operator<(const zavlahovac &z) const {
if (dir[0] == 'H') {
return y < z.y;
}
else return y > z.y;
}
};
struct node {
int start, range;
int sx, ex;
int sums;
node *prvy, *druhy;
node (int st, int rn, int n, vector<int> &coor) {
sx = (st < n ? coor[st] : infinity);
ex = (st + rn >= n ? infinity : coor[st + 1]);
start = st;
range = rn;
if (rn == 1) {
sums = 0;
prvy = NULL;
druhy = NULL;
}
else {
prvy = new node(st, rn / 2, n, coor);
druhy = new node(st + rn / 2, rn / 2, n, coor);
sums = 0;
}
}
node (node *old, node *newprvy, node *newdruhy, int newval) {
start = old -> start;
range = old -> range;
sx = old -> sx;
ex = old -> ex;
sums = newval;
prvy = newprvy;
druhy = newdruhy;
}
node *update(int p, int vl) {
if (range == 1) {
return new node(this, NULL, NULL, sums + vl);
}
if (druhy -> start <= p) return new node(this, prvy, druhy->update(p, vl), sums + vl);
return new node(this, prvy->update(p, vl), druhy, sums + vl);
}
int query(int st, int end) {
DBG cout << "In [" << sx << "; " << ex << "] [" << start << " range: " << range << "] sums = " << sums << " query(" << st << ", " << end << ")" << endl;
if (start >= end) return 0;
if (start + range <= st) return 0;
if (start >= st && start + range <= end) return sums;
return prvy->query(st, end) + druhy-> query(st, end);
}
void print(string k) {
cout << k << "In [" << start << "; " << start + range << "] with [" << sx << "; " << ex << "] sums = " << sums << endl;
if (range != 1) {
cout << k << "PRVY {\n";
prvy -> print(k + " ");
cout << k << "} DRUHY {\n";
druhy -> print(k + " ");
cout << k << "}" << endl;
}
}
};
struct intervalac {
int N;
int realn;
map<int, int> xcoors, ycoors;
vector<node *> roots;
string dir;
intervalac(int n, vector<zavlahovac> &zvs) {
if (!n) {
N = 0;
return;
}
N = pow(2, ceil(log2(n)));
realn = n;
dir = zvs[0].dir;
DBG cout << "intervalac " << dir << ":" << endl;
sort(zvs.begin(), zvs.end());
vector<int> xunsort;
FOR(i, n) {
ycoors[zvs[i].y] = i;
xunsort.push_back(zvs[i].x);
}
sort(xunsort.begin(), xunsort.end());
FOR(i, n) {
xcoors[xunsort[i]] = i;
}
roots.push_back(new node(0, N, n, xunsort));
FOR(i, n) {
DBG cout << "update " << i << " on pos " << xcoors[zvs[i].x] << endl;
roots.push_back(roots[i] -> update(xcoors[zvs[i].x], zvs[i].vlaha));
}
if (dir[0] == 'H') ycoors[infinity] = n;
DBG {
FOR(i, n + 1) {
cout << "Iteration " << i << ":" << endl;
roots[i] -> print("");
}
}
}
int query(int x, int y) {
if (!N) return 0;
if (dir[0] == 'H') {
auto it = ycoors.upper_bound(y);
int upto = (it == ycoors.begin() ? 0 : (--it)->second + 1);
if (dir[1] == 'L') {
auto itx = xcoors.lower_bound(x);
return (itx == xcoors.end() ? 0 : roots[upto] -> query(itx->second, N));
}
else {
DBG cout << "[" << x << "; " << y << " ] In " << dir << " upto = " << upto << " in " << ycoors << endl;
auto itx = xcoors.upper_bound(x);
return roots[upto] -> query(0, (itx == xcoors.end() ? N : itx -> second));
}
}
auto it = ycoors.lower_bound(y);
int yid = (it == ycoors.end() ? 0 : it -> second + 1);
if (dir[1] == 'L') {
auto itx = xcoors.lower_bound(x);
return (itx == xcoors.end() ? 0 : roots[yid] -> query(itx->second, N));
}
auto itx = xcoors.upper_bound(x);
DBG cout << "query (" << x << "; " << y << ") In " << dir << " yid = " << yid << " in " << ycoors << " and itx = " << (itx == xcoors.end() ? N : itx->second) << " from " << xcoors << endl;
return roots[yid] -> query(0, (itx == xcoors.end() ? N : itx -> second));
}
};
int main() {
cin.sync_with_stdio(false);
cout.sync_with_stdio(false);
int n = get<int>();
vector<zavlahovac> DL, DP, HP, HL;
FOR(i, n) {
int x, y;
int vl;
string smer;
cin >> x >> y >> vl >> smer;
if (smer == "DL") {
DL.push_back({x, y, vl, smer});
}
else if (smer == "DP") {
DP.push_back({x, y, vl, smer});
}
else if (smer == "HP") {
HP.push_back({x, y, vl, smer});
}
else HL.push_back({x, y, vl, smer});
}
intervalac iDL(DL.size(), DL);
intervalac iDP(DP.size(), DP);
intervalac iHL(HL.size(), HL);
intervalac iHP(HP.size(), HP);
int m = get<int>();
int k = get<int>();
int prev_ans = 0;
FOR(i, m) {
int x, y;
cin >> x >> y;
x ^= prev_ans * k;
y ^= prev_ans * k;
DBG cout << "Query " << i << ": " << x << " " << y << endl;
int idl = iDL.query(x, y);
int idp = iDP.query(x, y);
int ihl = iHL.query(x, y);
int ihp = iHP.query(x, y);
DBG cout << "DL: " << idl << " DP: " << idp << " HL: " << ihl << " HP: " << ihp << endl;
prev_ans = idl + idp + ihl + ihp;
cout << prev_ans << endl;
}
}Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.