Intervalový strom

Intervalový strom je dátová štruktúra, ktorá si, podobne ako obyčajné pole, pamätá postupnosť $n$ prvkov s indexami $0, 1, \dots, n-1$. Tieto prvky si pre jednoduchšie vyjadrovanie označme $p_0, p_1, \dots, p_{n-1}$. Intervalový strom dokáže robiť nasledovné operácie:

1. Pre zadanú hodnotu $h$ a index $i$ zmeniť hodnotu prvku $p_i$ na $h$, v čase $O(\log n)$.
2. Pre zadané $l, r$ (kde $0 \leq l \leq r < n$) odpovedať na otázku „aký je súčet čísel s indexami medzi $l$ a $r$?“ , v čase $O(\log n)$.

V druhej operácii môže byť namiesto sčítania ľubovoľná iná asociatívna operácia (napríklad súčin, maximum, minimum, najväčší spoločný deliteľ ...). Podľa toho potom hovoríme o súčtovom intervalovom strome, súčinovom intervalovom strome, maximovom intervalovom strome atď. Pre jednoduchosť budeme v tomto článku písať iba o súčtovom intervalovom strome. To, ako vyzerajú tie ostatné, si už ľahko domyslíte.

S použitím techniky lenivého šírenia informácie sa dá napísať intervalový strom, ktorý podporuje navyše ešte tretiu operáciu:

3. Pre zadané $l, r$ (a prípadne nejaké ďalšie parametre) zmeň hodnoty všetkých prvkov s indexami medzi $l$ a $r$ rovnakým spôsobom, v čase $O(\log n)$ (všimnite si, že časová zložitosť nezávisí od počtu prvkov, ktoré meníme).

To, ako presne môžeme touto operáciou meniť prvky, závisí od typu nášho stromu. Pri súčtovom intervalovom strome napríklad môžeme mať operáciu, ktorá nám umožní všetky prvky s indexami medzi $l$ a $r$ zvýšiť o rovnakú zadanú hodnotu $c$. O technike lenivého šírenia sa viac dočítate v samostatnom článku.

Štruktúra

Odteraz ďalej sa nám bude hodiť, aby počet prvkov $n$ našej postupnosti bola nejaká mocnina dvojky. V praxi, keď budeme chcieť použiť intervalový strom pre postupnosť s iným počtom prvkov, môžeme ju doplniť nulami na najbližšiu väčšiu mocninu dvojky. Postupnosť tým predĺžime nanajvýš dvakrát, takže asymptotickú časovú ani pamäťovú zložitosť nám to nezhorší.

Ako napovedá názov, intervalový strom má štruktúru stromu, konkrétne úplného binárneho stromu. Úplný binárny strom je zakorenený strom, v ktorom majú všetky listy rovnakú hĺbku a všetky vrcholy okrem listov majú práve dvoch synov (ľavého a pravého). Ľahko sa presvedčíme, že počet listov binárneho stromu je vždy nejaká mocnina dvojky. My použijeme strom s $n$ listami, v ktorých si budeme pamätať našu postupnosť prvkov $p_0, p_1, \dots, p_{n-1}$, pričom $p_0$ bude v najľavejšom liste, $p_1$ v druhom najľavejšom atď. Keďže náš strom má $n$ listov, jeho hĺbka bude $\lg n$ (kde symbolom $\lg$ označujeme dvojkový logaritmus).

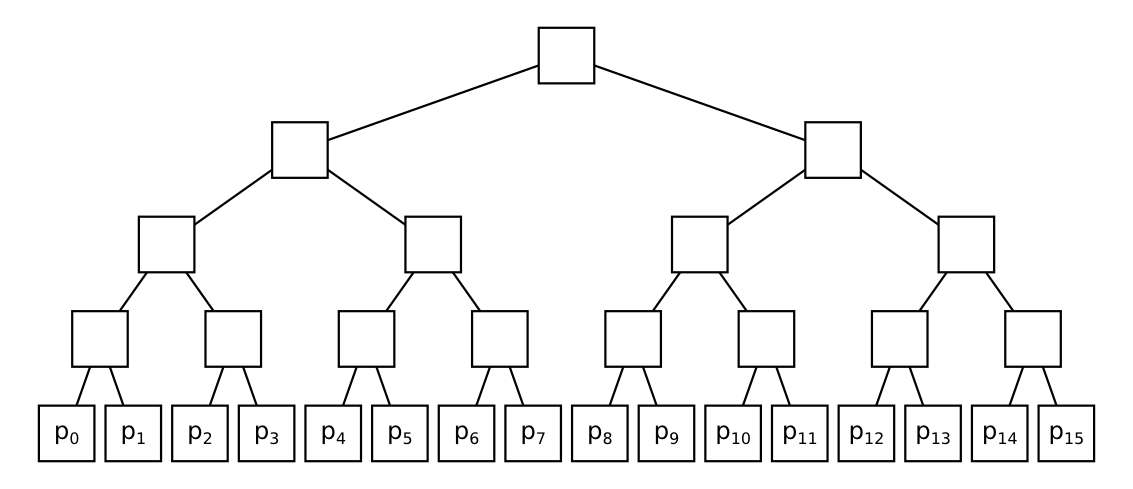
V každom vrchole, ktorý nie je list, si budeme pamätať súčet všetkých listov v jeho podstrome (teda listov, ktoré sú jeho potomkami). V koreni si teda budeme pamätať súčet všetkých $n$ prvkov $p_0 + p_1 + \dots + p_{n-1}$, v ľavom synovi koreňa si budeme pamätať súčet $p_0 + p_1 + \dots + p_{n/2-1}$, v pravom synovi koreňa bude súčet $p_{n/2} + \dots + p_{n-1}$ atď. Môžeme si všimnúť, že v každom vrchole (okrem listov) je vlastne súčet jeho synov. Zároveň platí, že v každom vrchole je súčet všetkých prvkov našej postupnosti s indexami z nejakého intervalu $[x, y)$ (budeme používať polootvorené intervaly, lebo sa tým vyhneme väčšine $\pm$ jednotiek, ktoré by nám znepríjemňovali implementáciu pri uzavretých intervaloch). Preto sa táto štruktúra nazýva intervalový strom.

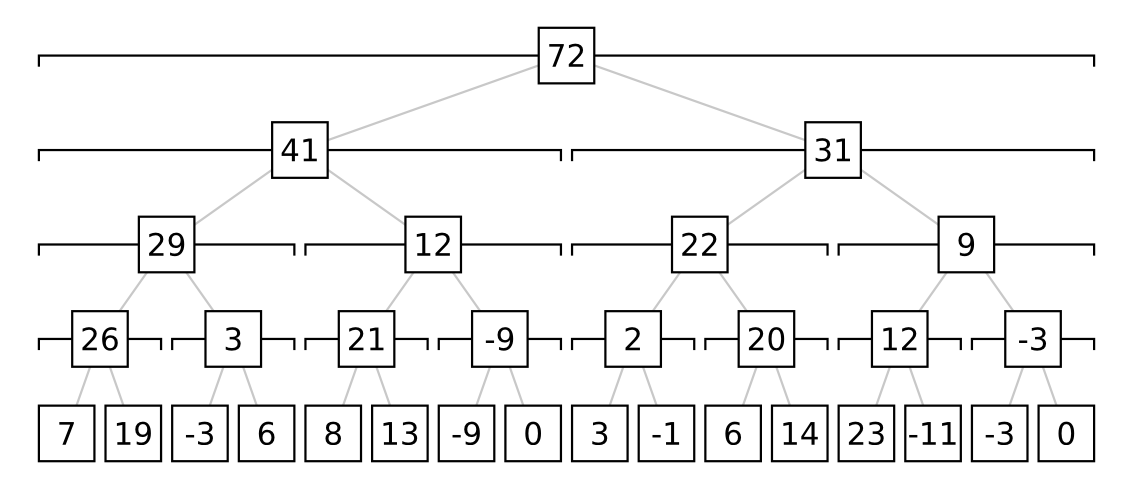
Náš strom má $n$ vrcholov na spodnom poschodí (listov), na pochodí o 1 vyššie má $n/2$ vrhcolov, na ďalšom poschodí má $n/4$ vrcholov atď. Dokopy má teda

$$n + \frac{n}{2} + \frac{n}{4} + \dots + 2 + 1 = 2n-1$$

vrcholov, čiže jeho pamäťová zložitosť bude $O(n)$.

Na intervalový strom sa môžeme pozerať ako na hierarchiu úradníkov. Každý vrchol je úradník, ktorý má na starosti nejaký úsek postupnosti $p_0, p_1, \dots, p_{n-1}$ a pamätá si jeho súčet. Každý úradník okrem listov má dvoch priamych podriadených -- svojich synov v strome. Ľavý syn sa stará o ľavú polovicu úseku svojho otca a pravý syn o pravú polovicu. Koreň má teda na starosti interval $[0, n)$, jeho synovia majú na starosti $[0, n/2)$ a $[n/2, n)$, $i$-ty list má na starosti iba prvok $p_i$, čo je vlastne interval $[i, i+1)$.

Operácie

Pozrime sa teraz, ako budú prebiehať jednotlivé operácie.

1. Zmena hodnoty prvku

Keď chceme zmeniť hodnotu prvku $p_i$, zmeníme hodnotu v príslušnom liste nášho stromu. Okrem toho potrebujeme ešte aktualizovať všetkých jeho nadriadených, lebo aj im sa zmenil súčet úseku, za ktorý sú zodpovední. To budeme robiť odspodu:

• Najprv sa pozrieme na otca $o_1$ vrcholu $p_i$ a aktualizujeme ho (priradíme doňho súčet jeho synov). V tomto vrchole je teraz už správna hodnota.
• Následne sa pozrieme na otca $o_2$ vrcholu $o_1$ (teda deda vrcholu $p_i$) a aktualizujeme ho (rovnako ako predtým, priradíme doňho súčet jeho synov). Keďže obaja jeho synovia mali správne hodnoty (vrchol $o_1$ je už aktualizovaný a druhého syna nebolo treba aktualizovať), vypočítaná nová hodnota vrcholu $o_2$ bude tiež správna.
• Pokračujeme otcom vrchola $o_2$, potom jeho otcom atď. až kým neprídeme do koreňa.

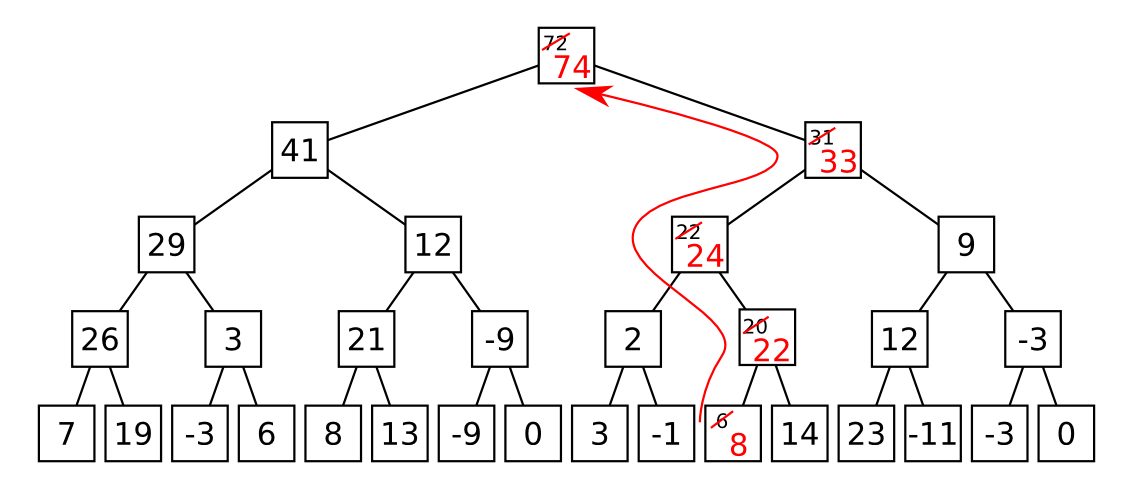
Keď už aktualizujeme aj koreň, všetci predkovia (nadriadení) vrcholu $p_i$ si budú pamätať správnu aktuálnu hodnotu a náš strom bude pripravený na ďalšie použitie. Keďže náš strom má $\lg n + 1$ úrovní, vrchol $p_i$ má $\lg n$ predkov, teda celá aktualizácia prebehne v čase $O(\lg n)$.

Všimnime si, že aktualizácia sa dá robiť aj inak: môžeme si vypočítať, o koľko sme zväčšili číslo $p_i$ a následne o rovnaké číslo zväčšiť všetkých jeho predkov (pričom je jedno v akom poradí ich zväčšujeme, pokojne to môžeme robiť aj zhora nadol). Takáto aktualizácia sa však nedá robiť vo všetkých druhoch intervalových stromov -- pri súčtovom funguje, ale napríklad pri minimovom nie. Preto je lepšie poznať predošlý spôsob.

2. Súčet prvkov z intervalu

Opäť použijeme našu paralelu s úradníckou hierarchiou. Od každého úradníka budeme chcieť, aby vedel odpovedať na otázky typu "Aký je súčet čísel, ktoré sú v tvojom úseku a majú indexy z intervalu $[l, r)$ ?" To vie úradník zodpovedný za nejaký úsek $[x, y)$ urobiť nasledovne:

1. Ak všetky prvky z $[x, y)$ ležia mimo $[l, r)$ (teda tieto dva intervaly sa neprekrývajú), potom odpovie 0.
2. Ak všetky prvky z $[x, y)$ ležia v $[l, r)$, potom je odpoveď súčet všetkých čísel s indexami z $[x, y)$. A tento súčet si predsa náš úradník pamätá.
3. Ak nenastane žiadna z predošlých možností (teda niektoré prvky z $[x, y)$ ležia v $[l, r)$ a niektoré nie), potom túto ťažkú otázku úradník v duchu zákona padajúceho exkrementu deleguje na svojich podriadených. Oboch svojich podriadených sa spýta, aký je súčet prvkov z ich úsekov, ktoré ležia v intervale $[l, r)$. Keďže úseky jeho podriadených akurát pokrývajú jeho úsek, stačí mu potom ich odpovede sčítať a dostane svoju odpoveď.

Všimnime si, že pri listoch tretí prípad nikdy nenastane -- každý list si totiž pamätá iba jeden prvok, ktorého index buď je, alebo nie je v $[l, r)$. Vďaka tomu sa nemôže stať, že by niekto, kto nemá podriadených, chcel delegovať svoju robotu na podriadených.

Správanie jednotlivých úradníkov sa dá ľahko implementovať ako rekurzívna funkcia. Keď chceme zistiť súčet prvkov s indexami z nejakého intervalu $[l, r)$, stačí sa na tento súčet spýtať koreňa (ktorý má na starosti celú postupnosť $p_0, p_1, \dots, p_{n-1}$), teda zavolať z neho našu rekurzívnu funkciu.

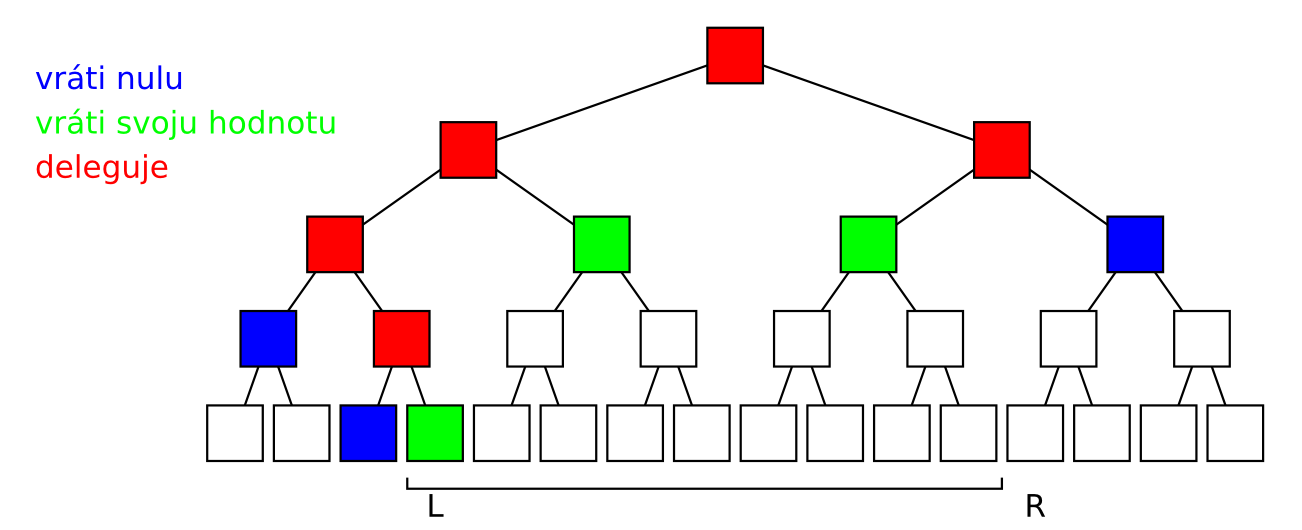
Aké rýchle to bude? Časová zložitosť bude úmerná počtu vrcholov, do ktorých sa naša funkcia postupne rekurzívne zavolá, keďže okrem rekurzívnych volaní v každom vrchole urobíme iba konštantne veľa práce (overíme, či nastala niektorá z prvých dvoch podmienok a prípadne ešte sčítame výsledky zo synov). Všimnime si, že na každej úrovni našej hierarchie budú najviac dvaja úradníci, ktorí svoju otázku delegujú na podriadených: ten, v ktorého úseku je ľavý koniec intervalu $[l, r)$ a ten, ktorý má vo svojom úseku pravý koniec intervalu $[l, r)$. U všetkých ostatných úradníkov z rovnakej úrovne, na ktorých sa naša rekurzívna funkcia zavolá, nastane buď prvý, alebo druhý prípad. Ak niektorý z koncov intervalu $[l, r)$ sadne presne na hranicu medzi úsekmi dvoch úradníkov, bude delegujúcich úradníkov na tejto úrovni ešte menej.

To ale znamená, že na každej úrovni budú najviac štyria úradníci, do ktorých sa naša funkcia zavolá -- podriadení úradníkov z úrovne o 1 vyššie, ktorí delegovali svoju otázku. Keďže náš strom má $\lg n + 1$ úrovní, dokopy sa naša rekurzívna funkcia zavolá najviac v $4 (\lg n + 1)$ vrcholoch, teda časová zložitosť celej operácie bude $O(\log n)$.

V konečnom dôsledku sme vlastne našli $O(\log n)$ úradníkov, ktorých intervaly dokopy dávajú interval $[l, r)$ a sčítali sme čísla v nich. Celá mašinéria s hierarchiou a delegovaním povinností nám slúžila iba na to, aby sme ich našli efektívne a pohodlne.

Implementácia

Existujú minimálne dva dobré spôsoby ako implemntovať intervalový strom:

• "V poli": celý strom si budeme pamätať v jednom poli. Výhodou tohto prístupu je kratší (a väčšinou rýchlejšie napísaný) kód. Nevýhodou je, že keď takýto intervalový strom chcete rozšíriť o ďalšiu funkcionalitu, kód začne byť nepríjemne zamotaný a ťažko čitateľný.

• Objektovo orientovaný: každý vrchol stromu bude jeden objekt a bude si pamätať referencie (smerníky) na svojich synov. Nevýhodou tohto spôsobu je trochu dlhší (a väčšinou pomalší) kód, výhodou je lepšia čitateľnosť kódu (ak sa kamarátite s objektovo orientovaným programovaním) a možnosť jednoduchého rozšírenia na perzistentný intervalový strom (čo je jedna zo silnejších verzií intervalového stromu).

Tu si ukážeme oba z nich.

Implementácia v poli

Vrcholy nášho stromu si môžeme očíslovať po riadkoch zhora nadol číslami $1, 2, \dots, 2n-1$:

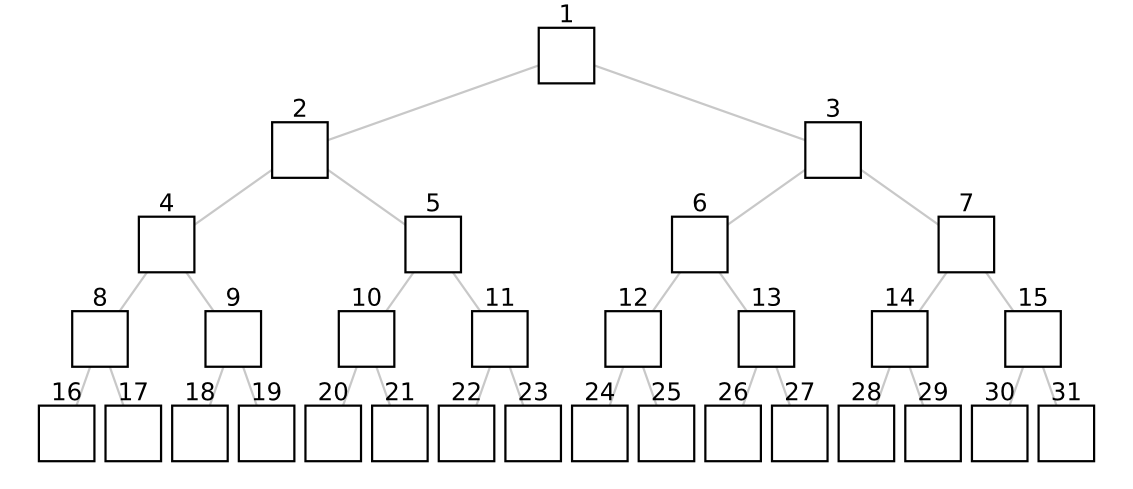
Toto číslovanie má jednu peknú vlastnosť: ak má vrchol číslo $x$, potom jeho synovia (ak nejakých má) majú čísla $2x$ a $2x+1$. Jeho otec má zasa číslo $\lfloor x/2 \rfloor$.

Vrcholy si teda môžeme pamätať v poli dĺžky $2n$, kde index $0$ nepoužijeme a inak bude na indexe $x$ vrchol číslo $x$. List číslo $i$ bude mať teda index $n+i$.

Okrem toho sa nám ešte zíde pamätať si začiatky a konce intervalov zodpovedajúcich jednotlivým vrcholom. Tie si vieme predpočítať do ďalších dvoch polí dĺžky $2n$, kde na indexe $x$ bude začiatok, resp. koniec intervalu zodpovedajúceho vrcholu $x$. Predpočítanie vieme urobiť v lineárnom čase postupujúc od vrcholu číslo $2n-1$ k vrcholu číslo 1:

• pre listy vypočítame hranice intervalov jednoducho
• interval každého vrcholu, ktorý nie je list, začína na rovnakom mieste ako interval jeho ľavého syna a končí na rovnakom mieste ako interval jeho pravého syna

Keďže postupujeme od väčších čísel vrcholov k menším, vždy, keď spracúvame nejaký vrchol, jeho synovia sú už spracovaní a teda môžeme využiť informáciu o začiatku a konci ich intervalov.

S takto uloženými dátami sa jednotlivé operácie implementujú pomerne priamočiaro.

class intervalovy_strom
{
    vector<int> strom; //hodnoty vrcholov v strome

    vector<int> zaciatok, koniec; //zaciatky a konce intervalov prisluchajucich 
                                  //jednotlivym vrcholom
    int n;

public:

    intervalovy_strom(int velkost) //konstruktor
    {
        n = 1;
        while(n < velkost) n *= 2; //najdeme najblizsiu vacsiu mocninu dvojky
        strom.resize(2*n, 0);

        zaciatok.resize(2*n); //predpocitame zaciatky a konce intervalov
        koniec.resize(2*n);
        for(int i=0; i<n; i++)
        {
            zaciatok[i+n] = i;
            koniec[i+n] = i+1;
        }
        for(int i=n-1; i>0; i--)
        {
            zaciatok[i] = zaciatok[i*2];
            koniec[i] = koniec[i*2+1];
        }
    }

    void zmen(int i, int h) //zmen hodnotu p_i na h
    {
        i += n;               //index i-teho listu
        strom[i] = h;

        //postupujeme zdola nahor po predkoch i-teho listu
        for(int predok = i/2; predok > 0; predok /= 2) 
        {
            strom[predok] = strom[predok*2] + strom[predok*2+1];
        }
    }

    //sucet prvkov s indexami z [l, r) pod vrcholom v
    int sucet(int l, int r, int v = 1) 
    {
        //nic co je pod vrcholom v nelezi v intervale [l, r)
        if(r <= zaciatok[v] || l >= koniec[v]) 
        {
            return 0; 
        }
        //vsetko pod vrcholom v je v intervale [l, r)
        if(r >= koniec[v] && l <= zaciatok[v]) 
        {
            return strom[v];
        }
        return sucet(l, r, v*2) + sucet(l, r, v*2+1); //delegovanie na synov
    }
};

Objektovo orientovaná implementácia

V tejto implementácii bude každý vrchol samostatný objekt, pamätajúci si referencie na svojich synov. Okrem toho môžeme mať jeden obaľujúci objekt reprezentujúci samotný strom, ktorý si pamätá referenciu na koreň a posúva mu všetky požiadavky.

Keď chceme zmeniť niektorý list $p_i$, nevieme to urobiť priamo (lebo si nepamätáme referencie na všetky listy, iba na koreň), ale požiadavku pošleme koreňu. Ten ju pošle tomu zo svojich synov, ktorý je predkom listu $p_i$, ten ju opäť deleguje na jedného zo svojich synov atď., až sa nakoniec dostane k listu $p_i$, ktorý si zmení hodnotu. Pri vynáraní z rekurzie sa vynárame cez predkov listu $p_i$, ktorých pritom môžeme rovno aktualizovať.

Implementácia je inak pomerne priamočiara.

class intervalovy_strom //vonkajsia trieda reprezentujuca cely strom
{
    class vrchol //trieda, ktorej instancie reprezentuju vrcholy
    {
        int hodnota;
        int zaciatok, koniec; //zaciatok a koniec mojho intervalu
        vrchol *lavy, *pravy; //smerniky na synov

    public:

        //konstruktor. Vytvori vrchol zodpovedajuci intervalu [zac, kon) 
        //aj s celym podstromom
        vrchol(int zac, int kon) : zaciatok(zac), koniec(kon) 
        {
            hodnota = 0;

            //ak este nie som list, vyrobim aj svojich synov s podstromami
            if(koniec - zaciatok > 1)  
            {
                int stred = (zaciatok + koniec)/2;
                lavy = new vrchol(zaciatok, stred);
                pravy = new vrchol(stred, koniec);
            }
            else //ak som list, tak nemam synov
            {
                lavy = pravy = NULL;
            }
        }

        void zmen(int i, int h)
        {
            if(zaciatok == i && koniec == i+1) //ak som i-ty list, zmenim si hodnotu
            {
                hodnota = h;
                return;
            }
            int stred = (zaciatok + koniec)/2;

            //ak je i-ty list v lavom podstrome, delegujem poziadavku lavemu synovi
            if(i < stred) lavy -> zmen(i, h);  
            else pravy->zmen(i, h);            //ak je v pravom, tak pravemu synovi

            //pri vynarani z rekurzie sa aktualizujem
            hodnota = lavy->hodnota + pravy->hodnota; 
        }

        int sucet(int l, int r)
        {
            if(l >= koniec || r <= zaciatok) return 0;
            if(l <= zaciatok && r >= koniec) return hodnota;
            return lavy->sucet(l, r) + pravy->sucet(l, r);  //delegovanie na synov
        }

        ~vrchol() //destruktor
        {
            if(lavy != NULL) delete lavy;
            if(pravy != NULL) delete pravy;
        }
    };

    vrchol *koren;

public:
    intervalovy_strom(int velkost)
    {
        int n = 1;
        while(n < velkost) n *= 2; //najdeme najblizsiu vacsiu mocninu dvojky
        koren = new vrchol(0, n);
    }

    void zmen(int i, int h)
    {
        koren->zmen(i, h);
    }

    int sucet(int l, int r)
    {
        return koren->sucet(l, r);
    }

    ~intervalovy_strom()
    {
        delete koren;
    }
};

Nakoniec ešte jedna zaujímavosť: pri takejto implementácii nepotrebujeme, aby $n$ bola mocnina dvojky, teda konštruktor triedy intervalovy_strom môže vyzerať aj takto:

    intervalovy_strom(int velkost)
    {
        koren = new vrchol(0, velkost);
    }

Porovnanie s inými prístupmi

Rovnaké operácie ako s intervalovým stromom vieme robiť aj inými spôsobmi, s inými časovými zložitosťami.

Prvky našej postupnosti si môžeme napríklad pamätať v obyčajnom poli. Zmena prvku na danom indexe je potom v čase $O(1)$, čo je rýchlejšie ako intervalový strom. Vypočítanie súčtu čísel na intervale $[l, r)$ však môže trvať až $O(n)$, keďže nám neostáva nič iné, než prejsť všetky prvky medzi $l$ a $r$ a pekne po jednom ich sčítať.

Ak by sme si prvky pamätali v poli a okrem toho k nim mali ešte predpočítané prefixové sumy, súčty intervalov by sme vedeli počítať v čase $O(1)$. Zmena prvku by nás však stála čas $O(n)$ (keďže po zmene jedného prvku by sme museli prepočítať veľkú časť prefixových súm).

Ak teda jednu z našich dvoch operácií (zmenu prvku, alebo výpočet súčtu) potrebujeme robiť veľakrát a druhú skoro vôbec, je efektívnejšie použiť niektorý z týchto jednoduchších prístupov.