Dvojrozmerné prefixové sumy

Tento článok je o zovšeobecnení techniky prefixových súm na dvojrozmerné polia. Táto technika nám umožňuje dvojrozmerné pole veľkosti $n \times m$ predspracovať v čase $O(n m)$ a následne vedieť v konštantnom čase odpovedať na otázky typu ,,Aký je súčet čísel v tomto obdĺžniku?''

Pri jednorozmerných prefixových sumách sme vypočítali pole čísel, kde na indexe i bol súčet prvých i čísel v pôvodnom poli p. V dvojrozmernom prípade máme nejaké dvojrozmerné pole d[n][m], teda pole s $n$ riadkami číslovanými (dohodnime sa, že zhora nadol) $0, 1, \dots, n-1$ a $m$ stĺpcami číslovanými (dohodnime sa, že zľava doprava) $0, 1, \dots, m-1$. Prefixové sumy pre toto pole budú vyzerať ako dvojrozmerné pole t[n+1][m+1], kde t[y][x] bude súčet čísel v obdĺžniku s y riadkami a x stĺpcami v ľavom hornom rohu poľa d, teda všetkých čísel v poli d s prvým indexom menším ako y a druhým indexom menším ako x.

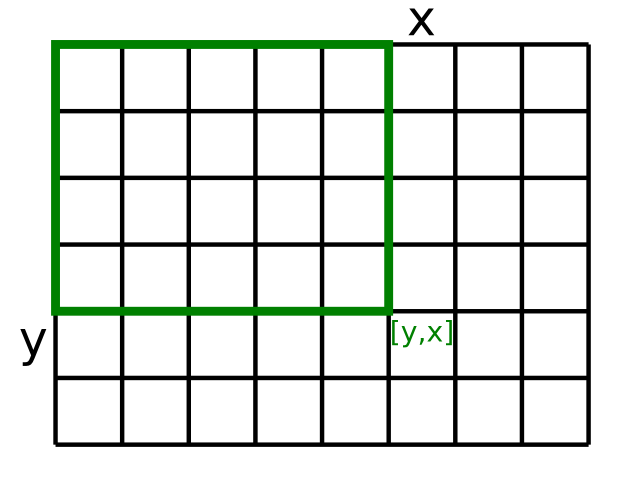
Ak by napríklad pole d vyzeralo nasledovne:

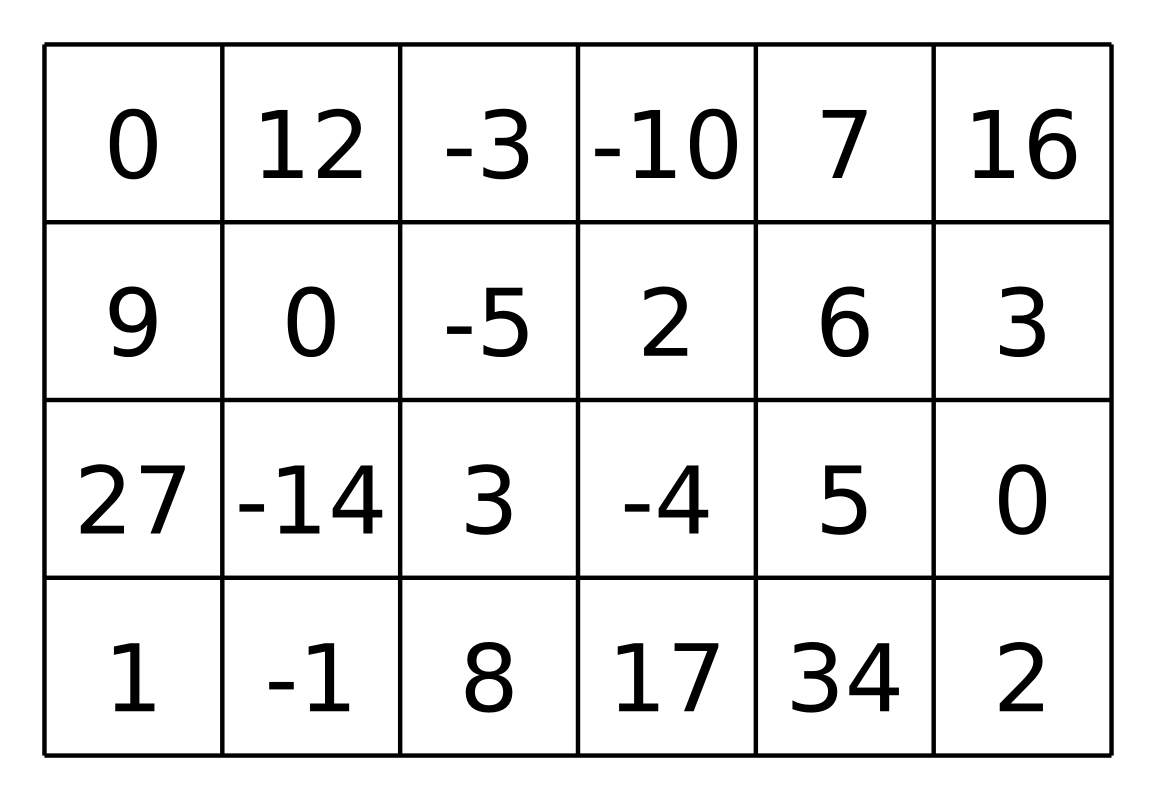
príslušné pole t by bolo takéto:

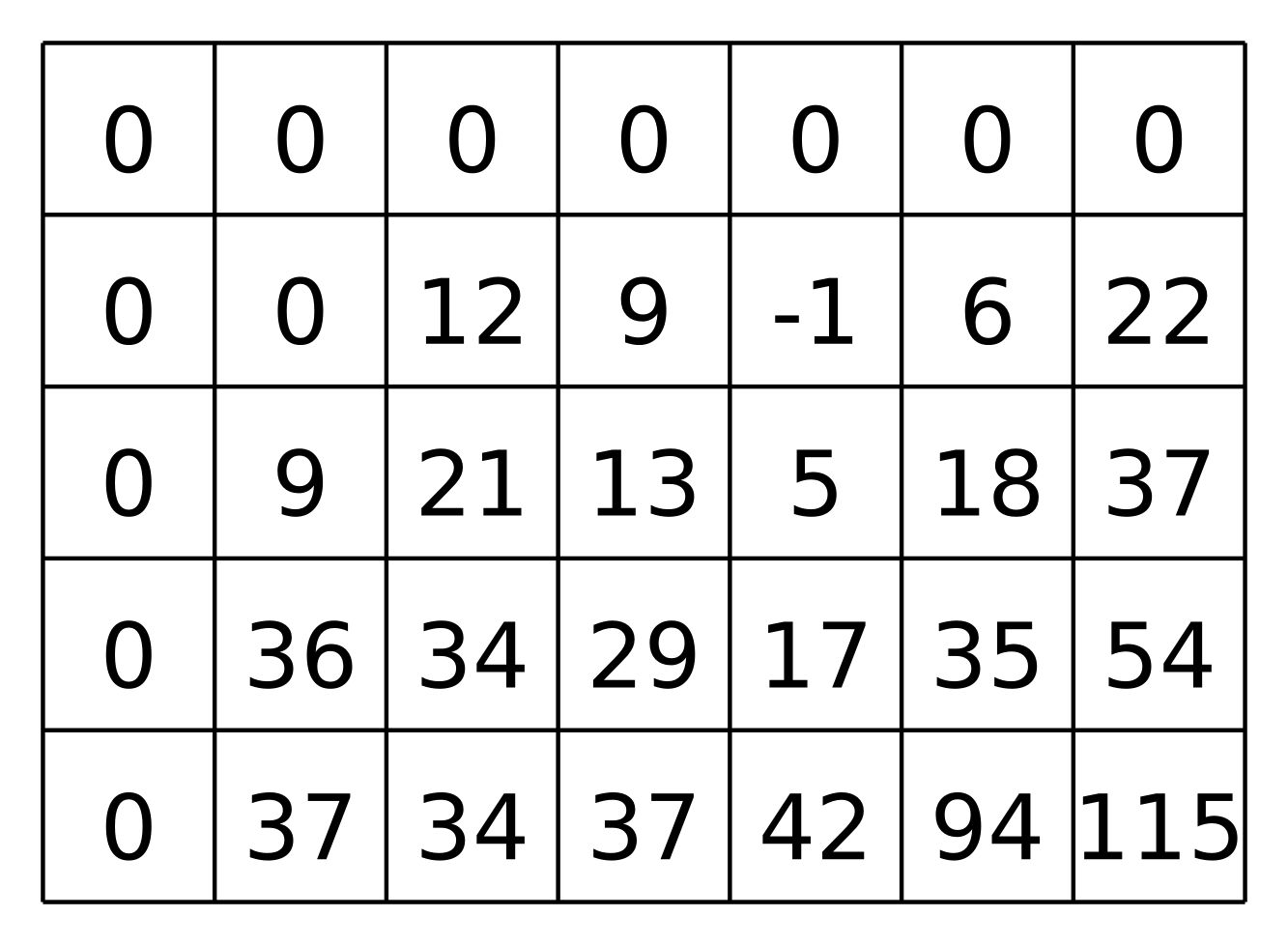
Počítanie 2D prefixových súm

Dvojrozmerné prefixové sumy sa dajú vypočítať v čase lineárnom od veľkosti poľa (teda v našom prípade $O(nm)$. Jedna možnosť je spočítať obyčajné jednorozmerné prefixové sumy po riadkoch a na výslednom poli spočítať prefixové sumy po stĺpcoch (rozmyslite si, prečo to bude fungovať). Dá sa to však aj pohodlnejšie, trikom. Uvedomme si, že (pre $x, y > 0$) číslo t[y][x] je dosť podobné číslu t[y-1][x], akurát do t[y][x] zarátavame navyše prvých $x$ čísel $y$-teho riadka (teda riadka s indexom y-1) poľa d.

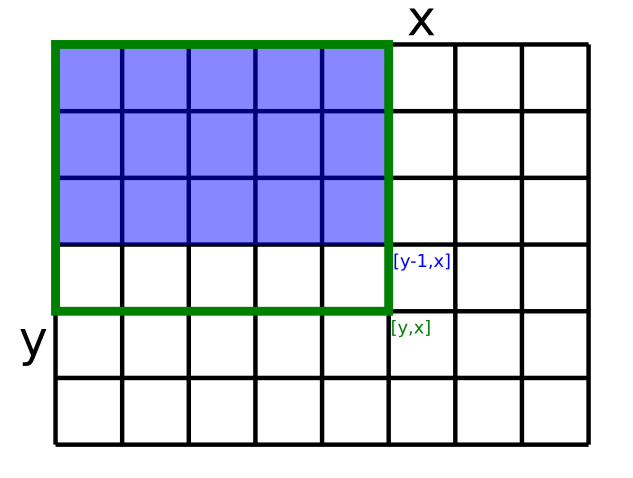
Zároveň je t[y][x] dosť podobné číslu t[y][x-1], líši sa od neho iba o súčet prvých $y$ čísel v $x$-tom stĺpci poľa d. Ak sčítame t[y-1][x] a t[y][x-1] a pripočítame ešte d[y-1][x-1], dostaneme súčet všetkých čísel v obdĺžniku s $y$ riadkami a $x$ stĺpcami v ľavom hornom rohu poľa d, akurát tam niektoré čísla budú zarátané dvakrát. Konkrétne to budú všetky čísla v obdĺžniku $(y-1) \times (x-1)$ v ľavom hornom rohu.

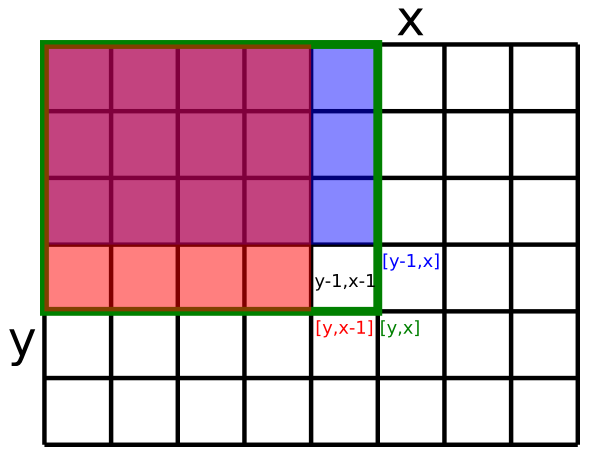
Súčet týchto čísel je vlastne prefixová suma t[y-1][x-1]. Stačí nám túto hodnotu odrátať a dostaneme súčet čísel v obdĺžniku $y \times x$ v ľavom hornom rohu, čo je hodnota t[y][x]. Hodnota t[y][x] teda bude rovná t[y-1][x] + t[y][x-1] + d[y-1][x-1] - t[y-1][x-1]. Pomocou tejto rovnosti môžeme pole t postupne po riadkoch (zhora nadol, v rámci riadka zľava doprava) vyplniť -- keď budeme vypĺňať t[y][x], všetky tri čísla t[y-1][x], t[y][x-1] aj t[y-1][x-1] už budeme poznať.

int n, m;
int d[n][m]; //vstupne pole
int t[n+1][m+1]; //pole, kam chceme ulozit prefixove sumy

for(int y=0; y<=n; y++) t[y][0] = 0; //nulty stlpec su nuly
for(int x=0; x<=m; x++) t[0][x] = 0; //nulty riadok su nuly
for(int y=1; y<=n; y++) {
    for(int x=1; x<=m; x++) {
        t[y][x] = t[y][x-1] + t[y-1][x] + d[y-1][x-1] - t[y-1][x-1];
    }
}

Využitie

Nakoniec si ešte ukážeme, ako s pomocou 2D prefixových súm vieme spočítať súčet čísel v ľubovoľnom obdĺžniku. Povedzme, že chceme spočítať súčet čísel v obdĺžniku, ktorého ľavé horné rohové políčko je d[y_1][x_1] a pravé dolné políčko je d[y_2][x_2]. Prefixová suma t[y_2+1][x_2+1] nám dá súčet všetkých čísel v obdĺžniku s ľavým horným rohom d[0][0] a pravým dolným rohom d[y_2][x_2]. To je väčší obdĺžnik, než sme chceli, preto od neho odrátame obdĺžnik s ľavým horným rohom v d[0][0] a pravým dolným rohom d[y_2][x_1-1], teda prefixovú sumu t[y_2+1][x_1]. Tým dostaneme súčet čísel v obdĺžniku s ľavým horným rohom d[0][x_1] a pravým dolným rohom d[y_2][x_2], čo je ešte stále väčší obdĺžnik, než by sme chceli. Potrebovali by sme ešte odčítať obdĺžnik s rohmi d[0][x_1] a d[y_1-1][x_2]. To nie je žiadna prefixová suma, vieme ho však dostať ako rozdiel t[y_1][x_2+1] - t[y_1][x_1]. 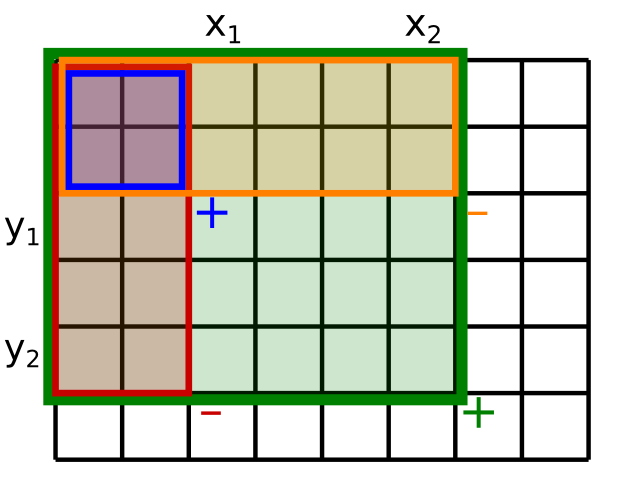Súčet čísel v obdĺžniku s rohmi d[y_1][x_1] a d[y_2][x_2] dostaneme ako t[y_2+1][x_2+1] - t[y_2+1][x_1] - t[y_1][x_2+1] + t[y_1][x_1]. Podobne ako pri jednorozmerných prefixových sumách, ak budeme používať polootvorené intervaly (teda obdĺžnik budeme zadávať súradnicami ľavého horného rohu a súradnicami najbližšieho políčka napravo dole od pravého dolného rohu), výraz sa ešte zjednoduší na t[y_2][x_2] - t[y_2][x_1] - t[y_1][x_2] + t[y_1][x_1].