7. Otoč sa!

Popri čakaní v rade profesionálne deformovanému grafovému teoretikovi niekedy napadne modelovať aj to čakanie v rade grafom. A takto vznikla táto úloha.

\(n\) ľudí stojí v rade na záchod. Teda, v rade ako rade¹. Tento rad má viac grafovej štruktúry ako by graf mal mať. Ľudia v rade sa na seba môžu pozerať. Ale pozerať sa na ľudí v “rade” nie je len tak! Menovite, pozeranie sa je tranzitívne: ak sa človek A pozerá na človeka B, a človek B sa pozerá na človeka C, potom sa aj človek A pozerá na človeka C. Navyše, žiadni dvaja ľudia sa na seba vzájomne nepozerajú, prípadný očný kontakt by bol príliš zahanbujúci!

Chceli by sme vedieť, či sa pri danej konfigurácií ľudí na seba ľudia vedia podľa hore uvedených pravidiel pozerať.

Úloha

Cyklus v (neorientovanom) grafe je postupnosť aspoň troch rôznych vrcholov, \(v_1\), \(v_2\), \(\dots\), \(v_k\) takých že medzi každými \(v_i\) a \(v_{i+1}\) je hrana a navyše \(v_1\) a \(v_k\) sú tiež spojené hranou. Kaktus je neorientovaný graf, v ktorom žiadna hrana neleží na viac ako jednom cykle.

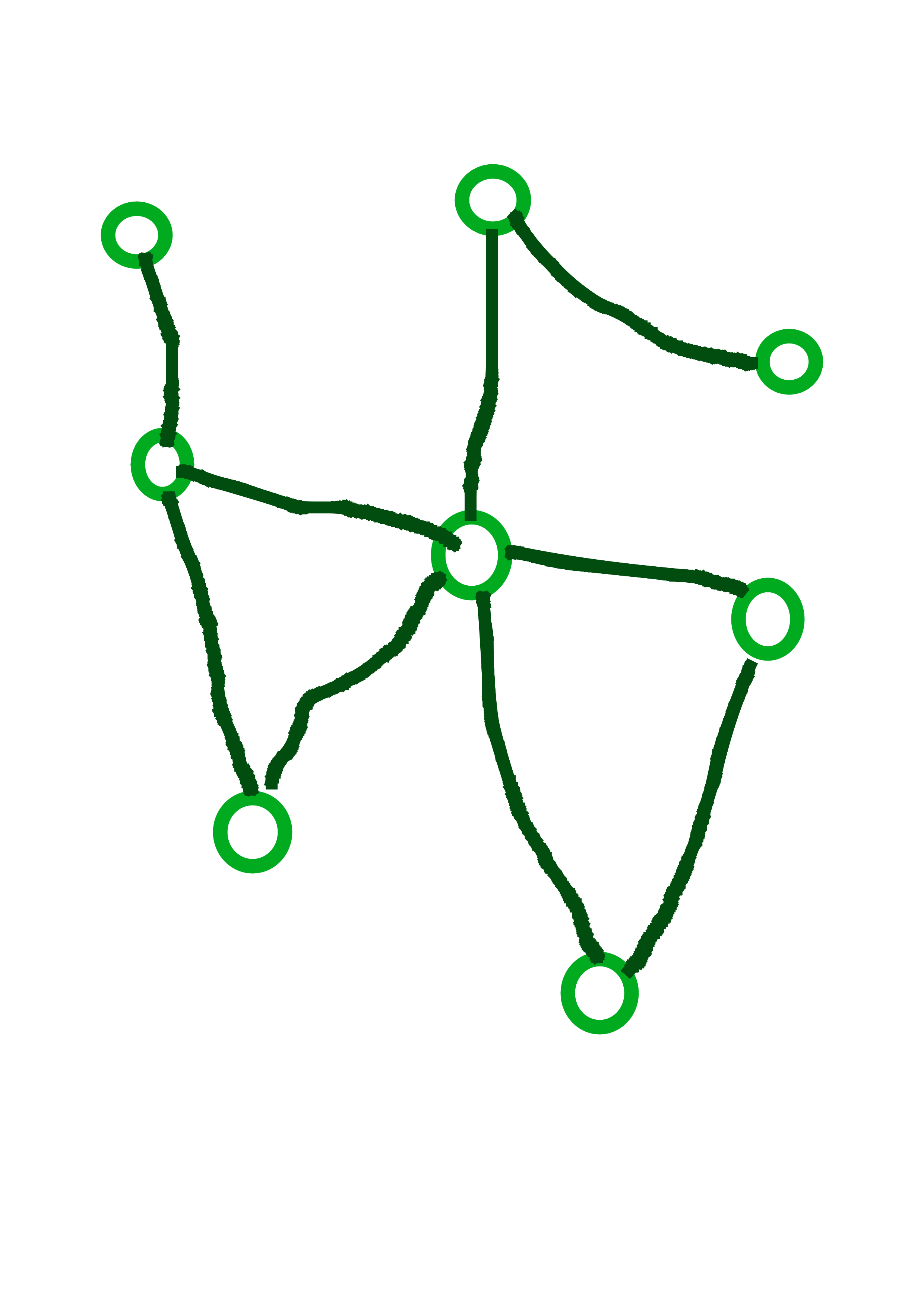
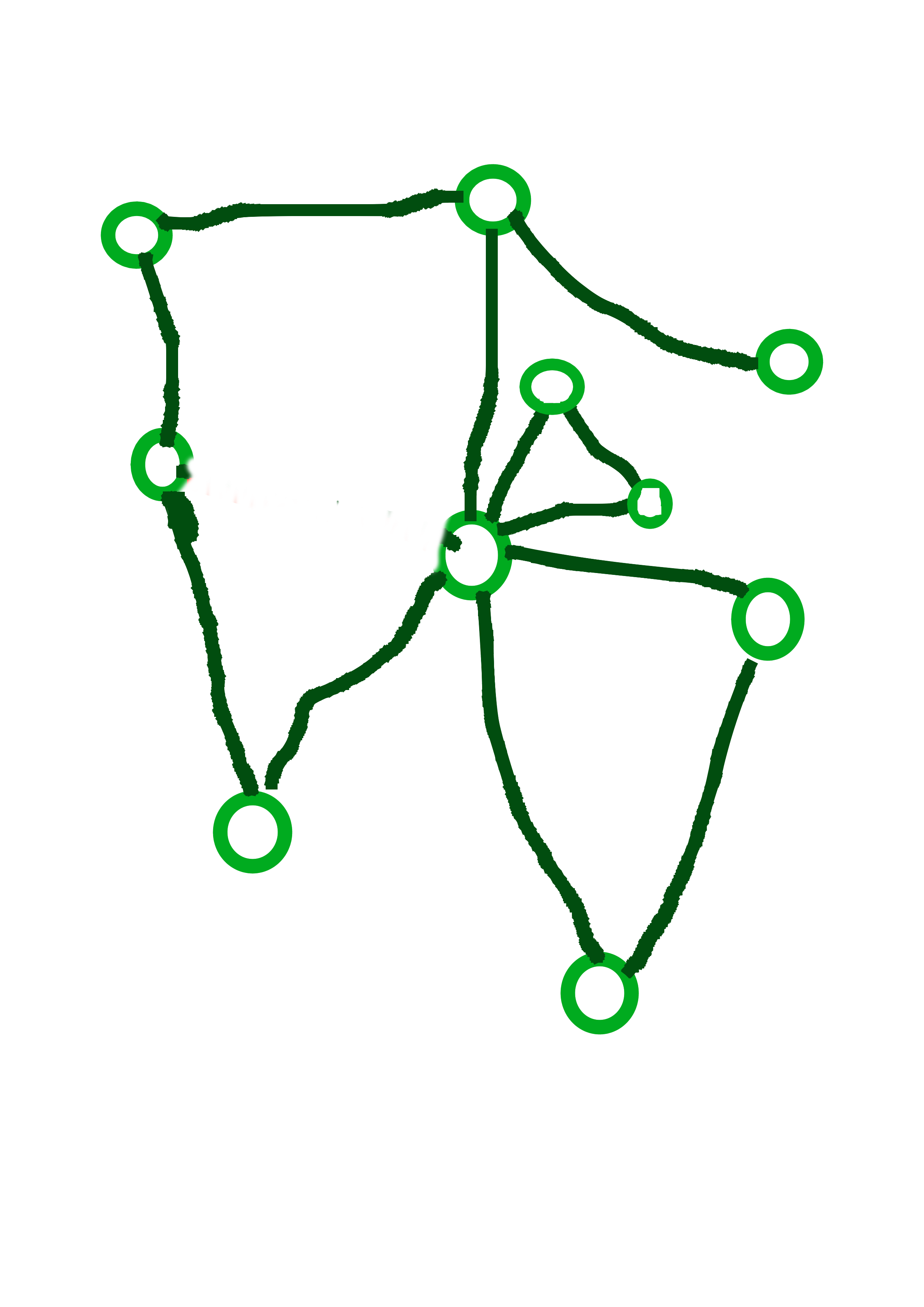
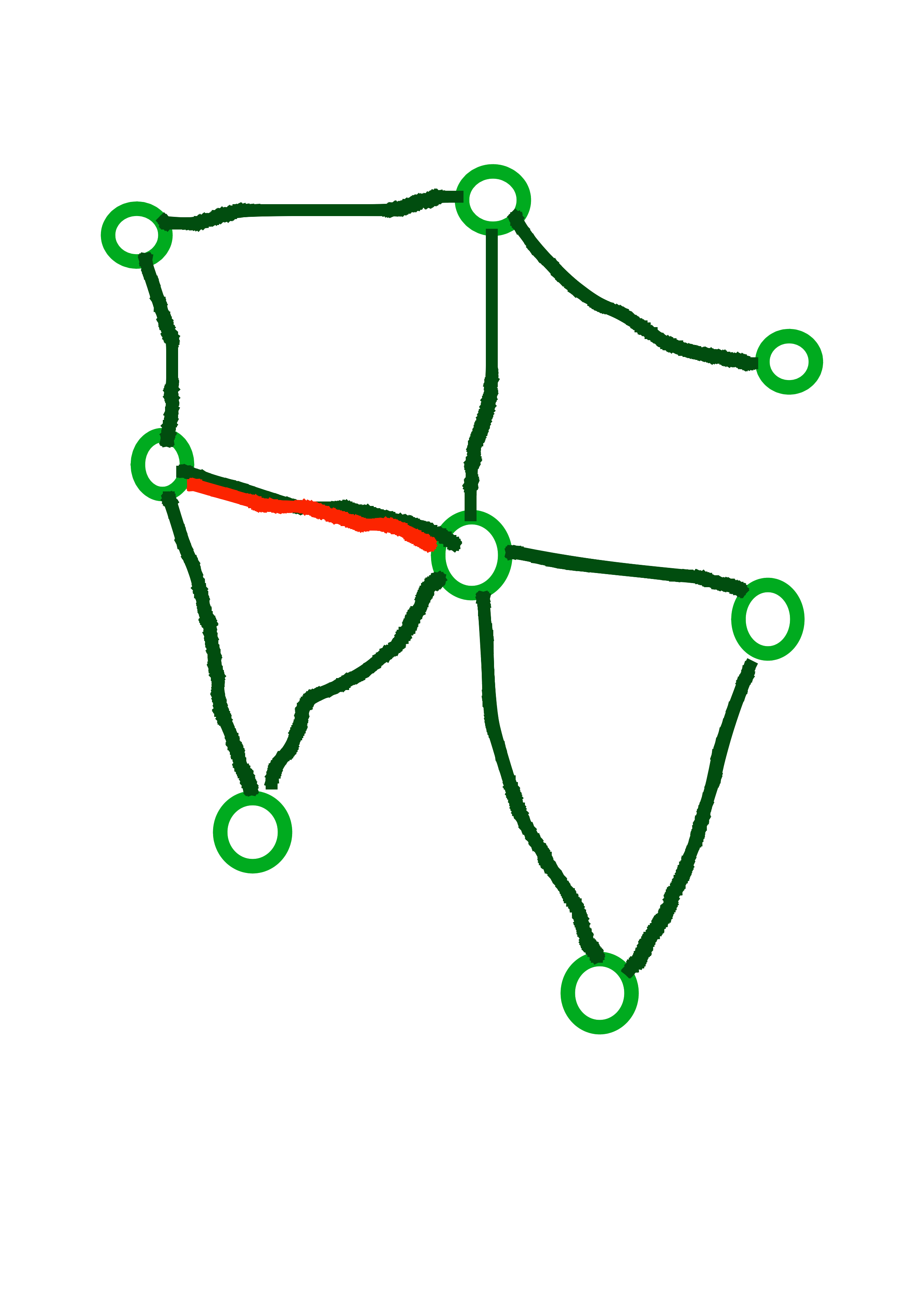
Na obrázkoch vidíme tri grafy, prvé dva z nich sú kaktusy. Posledný z nich nie je kaktus, pretože červená hrana leží na dvoch cykloch.

Na vstupe dostanete súvislý neorientovaný kaktus. Vrcholy predstavujú ľudí. Chceli by sme vedieť či vieme orientovať hrany - hrana z vrchola \(i\) do vrchola \(j\) hovorí, že človek \(i\) sa pozerá na človeka \(j\) - tak aby sa zachovala tranzitívnosť a acyklickosť.

Inak povedané, chceme dať každej hrane šípku tak, že:

• každá hrana je orientovaná presne jedným smerom
• výsledný orientovaný graf neobsahuje cyklus
• ak z \(i\) ide orientovaná hrana do \(j\), z \(j\) hrana do \(l\), potom ide aj z \(i\) orientovaná hrana do \(l\). Menovite to znamená, že potom hrana medzi \(i\) a \(l\) existuje v zadanom neorientovanom grafe.

Dá sa to? Ak áno, vypíšte ako.

Formát vstupu

Na prvom riadku vstupu sa nachádzajú dve medzerou oddelené čísla \(n\) a \(m\) – počet vrcholov zadaného kaktusu a počet jeho hrán.

Na ďalších \(m\) riadkoch sa nachádza popis hrán: na \(i\)-tom z nich sú dve rôzne čísla \(1 \leq a_i, b_i \leq n\) oddelené medzerou - vrcholy ktoré spája \(i\)-tá hrana.

Žiadna hrana sa na vstupe nevyskytuje viackrát.

Formát výstupu

Pokiaľ sa hrany orientovať nedajú vypíšte “nie” (bez úvodzoviek).

Pokiaľ sa hrany orientovať dajú, vypíste \(m+1\) riadkov: na prvom z nich vypíšte “ano” (bez úvodzoviek) a na ďalších \(m\) riadkoch vypíšte orientované hrany. Nemusia ísť v poradí akom boli na vstupe, ale všetky hrany zo vstupu musia byť takto zorientované. \(a b\) znamená že z vrcholu \(a\) ide hrana do vrcholu \(b\).

Hodnotenie

Sú 4 sady vstupov. Platia v nich nasledovné obmedzenia:

Navyše, v tretej sade platí, že \(m = n - 1\), teda zadaný kaktus je strom (neobsahuje žiadne cykly).

Príklady

Input:

5 5
1 2
3 2
2 4
5 4
3 5

Output:

ano
1 2
3 2
4 2
3 5
4 5

Ľudia vo vrcholoch \(2\) a \(5\) sa na nikoho pozerajú, naopak, všetci ich susedia hľadia na nich

Input:

8 9
7 8
8 1
7 1
1 5
1 2
2 3
3 4
4 5
4 6

Output:

nie

Nech robíme, čo robíme, nevieme otočiť hrany tak, aby všetky tri podmienky platili