7. Otoč sa! (vzorové riešenie) - Korešpondenčný seminár z programovania

Zadanie

Popri čakaní v rade profesionálne deformovanému grafovému teoretikovi niekedy napadne modelovať aj to čakanie v rade grafom. A takto vznikla táto úloha.

\(n\) ľudí stojí v rade na záchod. Teda, v rade ako rade¹. Tento rad má viac grafovej štruktúry ako by graf mal mať. Ľudia v rade sa na seba môžu pozerať. Ale pozerať sa na ľudí v “rade” nie je len tak! Menovite, pozeranie sa je tranzitívne: ak sa človek A pozerá na človeka B, a človek B sa pozerá na človeka C, potom sa aj človek A pozerá na človeka C. Navyše, žiadni dvaja ľudia sa na seba vzájomne nepozerajú, prípadný očný kontakt by bol príliš zahanbujúci!

Chceli by sme vedieť, či sa pri danej konfigurácií ľudí na seba ľudia vedia podľa hore uvedených pravidiel pozerať.

Úloha

Cyklus v (neorientovanom) grafe je postupnosť aspoň troch rôznych vrcholov, \(v_1\), \(v_2\), \(\dots\), \(v_k\) takých že medzi každými \(v_i\) a \(v_{i+1}\) je hrana a navyše \(v_1\) a \(v_k\) sú tiež spojené hranou. Kaktus je neorientovaný graf, v ktorom žiadna hrana neleží na viac ako jednom cykle.

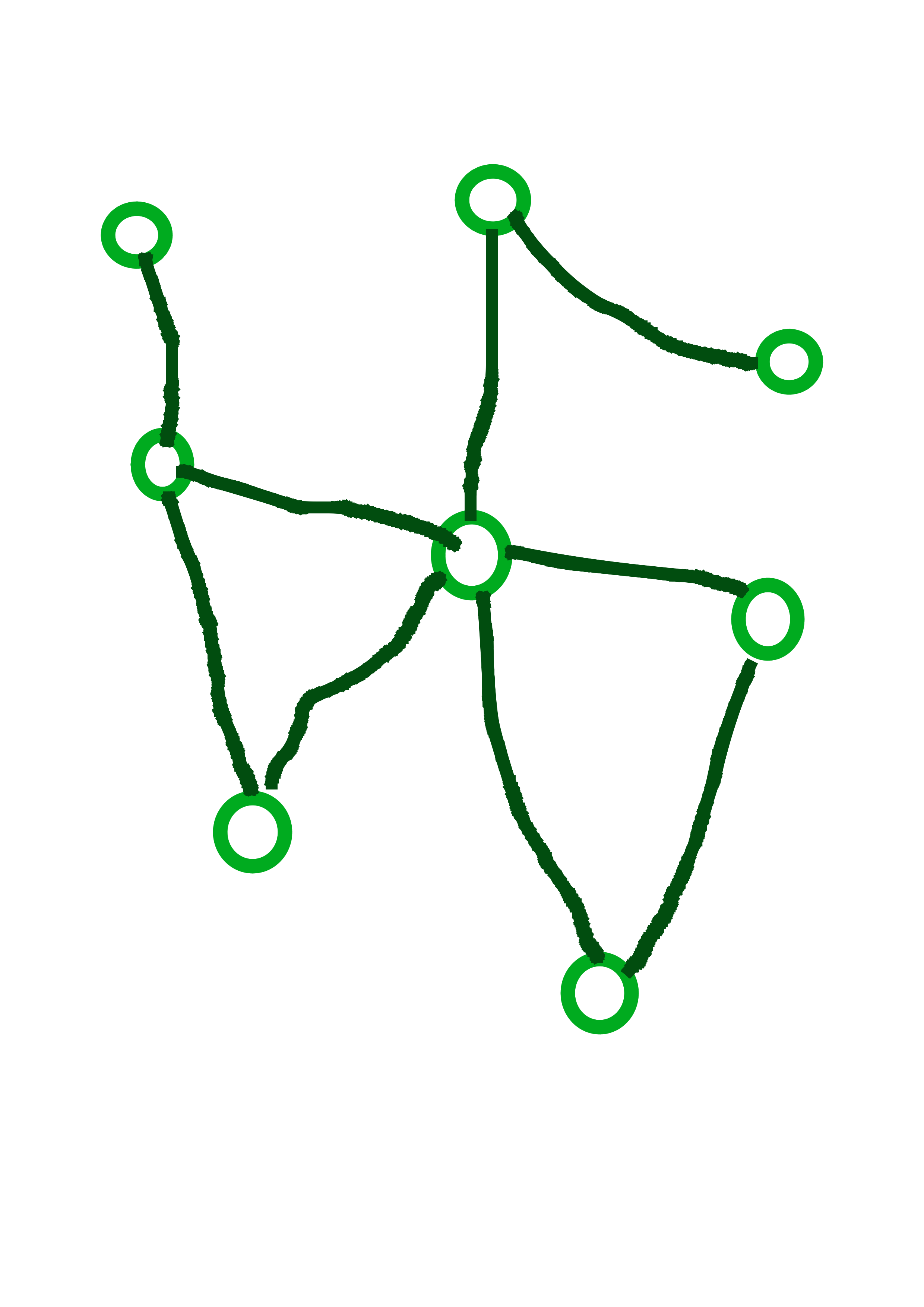
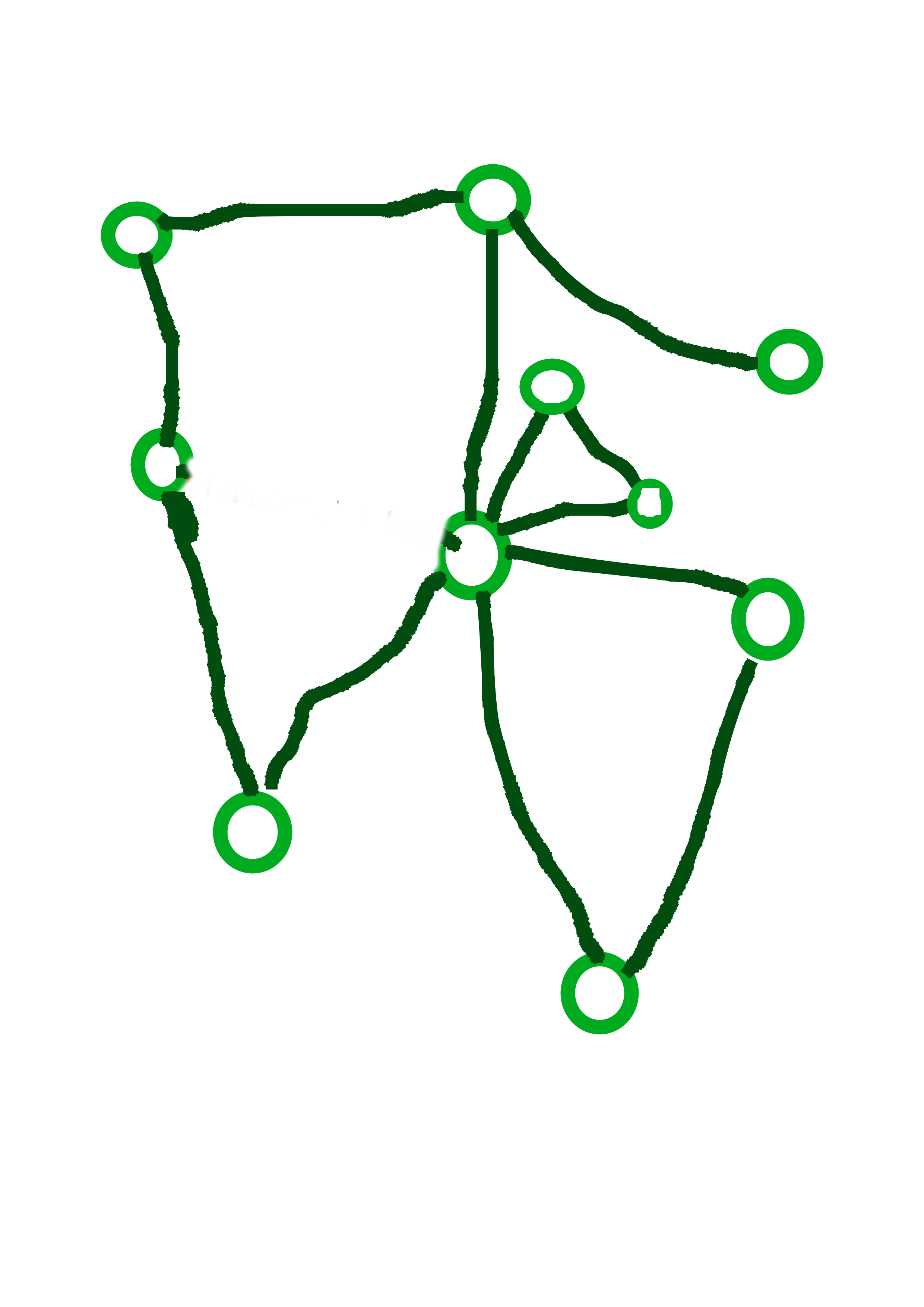
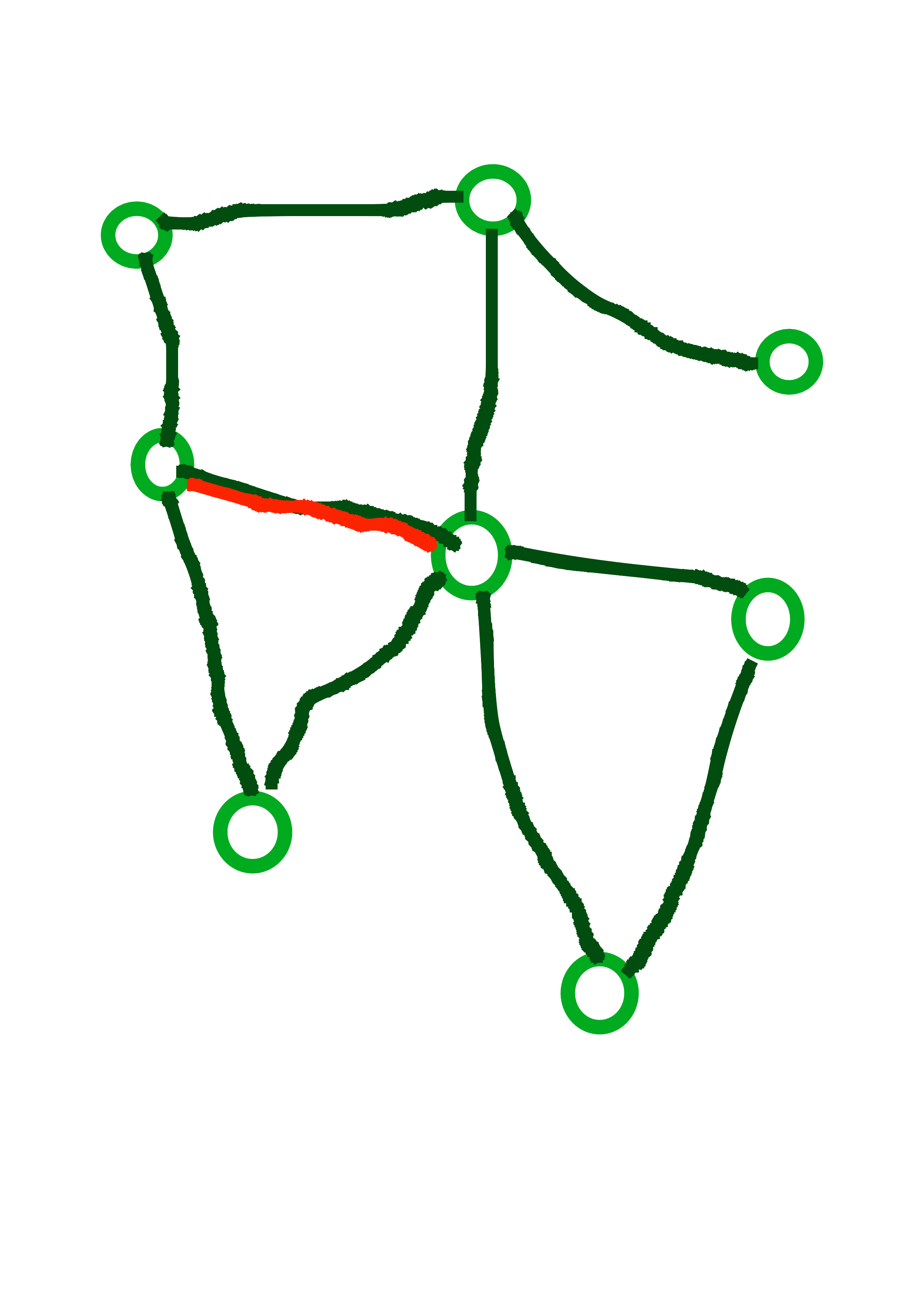
Na obrázkoch vidíme tri grafy, prvé dva z nich sú kaktusy. Posledný z nich nie je kaktus, pretože červená hrana leží na dvoch cykloch.

Na vstupe dostanete súvislý neorientovaný kaktus. Vrcholy predstavujú ľudí. Chceli by sme vedieť či vieme orientovať hrany - hrana z vrchola \(i\) do vrchola \(j\) hovorí, že človek \(i\) sa pozerá na človeka \(j\) - tak aby sa zachovala tranzitívnosť a acyklickosť.

Inak povedané, chceme dať každej hrane šípku tak, že:

každá hrana je orientovaná presne jedným smerom
výsledný orientovaný graf neobsahuje cyklus
ak z \(i\) ide orientovaná hrana do \(j\), z \(j\) hrana do \(l\), potom ide aj z \(i\) orientovaná hrana do \(l\). Menovite to znamená, že potom hrana medzi \(i\) a \(l\) existuje v zadanom neorientovanom grafe.

Dá sa to? Ak áno, vypíšte ako.

Formát vstupu

Na prvom riadku vstupu sa nachádzajú dve medzerou oddelené čísla \(n\) a \(m\) – počet vrcholov zadaného kaktusu a počet jeho hrán.

Na ďalších \(m\) riadkoch sa nachádza popis hrán: na \(i\)-tom z nich sú dve rôzne čísla \(1 \leq a_i, b_i \leq n\) oddelené medzerou - vrcholy ktoré spája \(i\)-tá hrana.

Žiadna hrana sa na vstupe nevyskytuje viackrát.

Formát výstupu

Pokiaľ sa hrany orientovať nedajú vypíšte “nie” (bez úvodzoviek).

Pokiaľ sa hrany orientovať dajú, vypíste \(m+1\) riadkov: na prvom z nich vypíšte “ano” (bez úvodzoviek) a na ďalších \(m\) riadkoch vypíšte orientované hrany. Nemusia ísť v poradí akom boli na vstupe, ale všetky hrany zo vstupu musia byť takto zorientované. \(a b\) znamená že z vrcholu \(a\) ide hrana do vrcholu \(b\).

Hodnotenie

Sú 4 sady vstupov. Platia v nich nasledovné obmedzenia:

Sada	1	2	3	4
\(2 \leq n, m \leq\)	\(20\)	\(1000\)	\(10^5\)	\(10^5\)

Navyše, v tretej sade platí, že \(m = n - 1\), teda zadaný kaktus je strom (neobsahuje žiadne cykly).

Príklady

Input:

Output:

Ľudia vo vrcholoch \(2\) a \(5\) sa na nikoho pozerajú, naopak, všetci ich susedia hľadia na nich

Input:

Output:

nie

Nech robíme, čo robíme, nevieme otočiť hrany tak, aby všetky tri podmienky platili

zoradiť sa prirodzene do radu sa pre niektorých ľudí ukazuje ako veľmi ťažká úloha. Ale o tom táto úloha nie je.↩︎

Keď je kaktus stromom

Pozrime sa najskôr na to, ako vyriešiť tretiu sadu: keď zadaný graf je strom.

Ukáže sa, že stromy vieme orientovať vždy nasledovným algoritmom:

Zakoreňme strom a pre každý vrchol spočítame jeho hĺbku (vzdialenosť od vrchola).
Všetky hrany orientujeme tak, aby išli z nepárnej hĺbky do párnej hĺbky

Každý vrchol po tomto orientovaní má buď všetky hrany idúce do neho, alebo z neho. Takto neexistuje cesta (po orientovaných hranách) s dĺžkou dva (alebo viac). Taktiež sa nevyskutuje cyklus, keďže stromy žiadne cykly nemajú.

Tento algoritumus vieme implementovať v čase aj pamäti \(O(n)\) , napríklad pomocou prehľadávania do hĺbky.

Čo s cyklami?

Najskôr sa zamyslime, čo sa deje, ak je zadaný kaktus cyklom.

Všimnime si, že akonáhle máme cyklus veľkosti viac ako \(3\), nemôžeme mať cestu dĺžky dva, teda hranu z \(a\) to \(b\) a zároveň hrany z \(b\) do \(c\). Je to preto, že potom by sme museli mať aj hranu z \(a\) do \(c\). Lenže, ak už hrana z \(a\) do \(b\) leží na väčšom cykle, nemôže ležať na ďalšom cykle (\(a-b-c\)), keďže zadaný graf je kaktus. Takže, každý vrchol ležiaci v cykle dĺžky väčšej než \(3\) má buď všetky hrany idúce z neho, alebo do neho.

Keď je dĺžka cyklu párna, potom vieme orientovať hrany na striedačku: každý druhý vrchol má všetky jeho hrany idúce z neho, a ostatné vrcholy v cykle majú všetky hrany idúce z nich, ako môžme vidieť na obrázku.

Čo ak je cyklus nepárnej dĺžky? Potom tento istý postup nemôžeme spraviť. Všimnime si navyše, že akonáhle orientujeme jednu hranu v cykle, orientácia ostatných hrán v cykle je daná - tak, aby sme nespravili cyklus. Problém je, že orientácia hrán “na striedačku” v nepárnom cykle nefunguje (skúste si to). Takže akonáhle máme nepárny cyklus dĺžky väčšej ako tri, nevieme ho orientovať.

Z toho vyplýva, že keď graf obsahuje nepárny cyklus dlhší než tri, nejde ho zorientovať.

Čo s cyklami dĺžky tri? Všimnime si, že ich hrany vieme orientovať hocijako. Bez ohľadu na ich orientovanie, vždy ostane jeden vrchol do ktorého hrany prichádzajú, jeden z ktorého odchádzajú a jeden, do ktorého jedna hrana pricháda a druhá odchádza. Rozmyslite si, prečo sú tak všetky podmienky zo zadania splnené.

Všetko dokopy

Vyššie v texte sme si všimli, že ak graf obsahuje nepárny cyklus veľkosti \(5\) alebo viac, potom hrany orientovať nejde. Ide to inak vždy? Nie, ukáže sa, že je ešte jeden prípad, v ktorom to nejde. Predstavme si, že graf obsahuje cyklus dĺžky tri, taký, že z každého vrchola tohto cyklu ide aspoň jedna ďalšia hrana. Lenže, ako sme pozorovali vyššie, akokoľvek orientujeme hrany v trojcykle, bude mať presne jeden vrchol, ktorý je v strede cesty dĺžky dva (teda jedna hrana troj-cyklu ide doňho, a ďalšia z neho). Problém je s hranami v tomto vrchole, ktoré nie sú hrany trojcyklu. Keďže zadaný graf je kaktus, hrany trojcyklu neležia na žiadnom ďalšom cykle. Z toho nám vyjde, že tieto ďalšie hrny orientovať nevieme (rozmyslite si to).

Ukáže sa, že toto je naozaj posledný prípad kedy to nejde. Na algoritmus nám ďalej poslúži nasledovné pozorovanie: keď zoberieme dobre-orientovaný graf (spĺňajúci podmienky v zadaní), a otočíme všetky hrany, dostaneme taktiež dobre-orientovaný graf. Teda nezáleží na tom, ako zorientujeme prvú hranu.

Algoritmus bude podobný ako pre stromy: zvolíme si ľubovoľne orientáciu prvej hrany, a takto sa nám jednoznačne zadá orientácia (takmer) všetkých ostatných hrán. Jediné, kde môžeme mať voľbu sú troj-cykly. V nich treba vybrať ktorý vrchol bude mať jednu príchodziu a jednu odchádzajúcu hranu, a tento vrchol musí mať stupeň presne \(2\). Jediné, na čo si treba dávať pozor sú trojuholníky - tam treba vybrať orientáciu hrán, (teda aby z neho išli len grafy trojcyklu).

Najskôr skontrolujme (napríklad prehľadávaním do hĺbky), či v grafe neexistuje nepárny cyklus dĺžky aspoň \(5\), alebo troj-cyklus, ktorý neobsahuje vrchol stupňa dva.
Prehľadávame do hĺbky: pre vrcholy vo vrstvách dfs-stromu alternujeme, či idú hrany z nich, či do nich. Treba si dávať pozor na trojuholníky, tie ošetríme špeciálne: vyberieme jeden – ak ich je viac, z jeho vrcholov ktorý má stupeň dva, jednu hranu orientujeme doňho, a druhú z neho.

Všetko sa dá spraviť napríklad dvoma prehľadávaniami do hĺbky, v časovej aj pamäťovej zložitosti \(O(n)\).

#include<bits/stdc++.h>

using namespace std;

#define FOR(i,n)	for(int i=0;i<(int)n;i++)
#define FOB(i,n)	for(int i=n;i>=1;i--)
#define MP(x,y)	make_pair((x),(y))
#define ii pair<int, int>
#define lli long long int
#define ld long double
#define ulli unsigned long long int
#define lili pair<lli, lli>
#ifdef EBUG
#define DBG	if(1)
#else
#define DBG	if(0)
#endif
#define SIZE(x) int(x.size())
const int infinity = 2000000999 / 2;
const long long int inff = 4000000000000000999;

typedef complex<long double> point;

template<class T>
T get() {
    T a;
    cin >> a;
    return a;
}

template <class T, class U>
ostream& operator<<(ostream& out, const pair<T, U> &par) {
    out << "[" << par.first << ";" << par.second << "]";
    return out;
}

template <class T>
ostream& operator<<(ostream& out, const set<T> &cont) {
    out << "{";
    for (const auto &x:cont) out << x << ", ";
    out << "}";
    return out;
}

template <class T, class U>
ostream& operator<<(ostream& out, const map<T,U> &cont) {
    out << "{";
    for (const auto &x:cont) out << x << ", ";
    
    out << "}"; return out;
}

template <class T>
ostream& operator<<(ostream& out, const vector<T>& v) {
    FOR(i, v.size()){
      if(i) out << " ";
      out << v[i];
    }
    out << endl;
    return out;
}

bool ccw(point p, point a, point b) {
    if((conj(a - p) * (b - p)).imag() <= 0) return false;
    else return true;
}

pair<ii, bool> treeify(int v, int f, int h, vector<int> &H, vector<ii> &parcyc, vector<vector<int> > &hrany) {
    H[v] = h;
    DBG cout << "In " << v << " with height " << h << endl;
    
    for (int w : hrany[v]) {
        if (w == f) continue;
        if (H[w] != -1) {
            if (H[w] > H[v]) continue;
            int cycle = h - H[w] + 1;
            DBG cout << "Cycle detected in " << v << " backedge to " << w << " of len " << cycle << endl;
            if (cycle > 3 && (cycle % 2) == 1) return {{v, w}, 0};
            
            parcyc[v] = {v, w};

        }
        else {
            auto res = treeify(w, v, h + 1, H, parcyc, hrany);
            if (!res.second) return {res.first, 0};
            // if f-v is in the cycle
            if (res.first.first != v && res.first.second != v && res.first.first >= 0) {
                parcyc[v] = res.first;
            }
        }
    }
    return {parcyc[v], 1};
}

bool otoc(int v, int f, bool into, vector<int> &H, vector<ii> &parcyc, vector<vector<int> > &hrany, set<ii> &oriented) {
    int cycle_len = (parcyc[v].first >= 0 ? H[parcyc[v].first] - H[parcyc[v].second] + 1 : 1);
    
    DBG cout << "In  " << v << " pointing into ? " << into << " and cycle len " << cycle_len << endl;
    
    if (cycle_len != 3 || hrany[v].size() > 2) {
        for (int w : hrany[v]) {
            if (w == f) {
                DBG cout << "vf ? " << oriented.count({v,w}) << " and fv " << oriented.count({w, v}) << endl;
                if (into && oriented.count({v, w})) return 0;
                if ((!into) & oriented.count({w, v})) return 0;
                continue; // sorted
            }
            if (into) {
                if (oriented.count({v, w})) {
                    DBG cout << "Problem: {" << v << ", " << w << "} in oriented" << endl;
                    return 0;
                }
                oriented.insert({w, v});
            }
            else {
                if(oriented.count({w, v})) {
                    DBG cout << "Problem: {" << w << ", " << v << "} in oriented" << endl;
                    return 0;
                }
                oriented.insert({v, w});
            }
        }
        for (int w : hrany[v]) {
            if (parcyc[v] == MP(v, w) || w == f) continue;
            if (parcyc[w] != MP(w, v)) { // o/w it's taken care of
                DBG cout << v << "-> " << w << endl;
                if (!otoc(w, v, !into, H, parcyc, hrany, oriented)) {
                    DBG cout << "From " << w << " reported failure " << endl;
                    return 0;
                }
            }
        }
    }
    else {
        DBG cout << "in 3-cycle " << endl;
        int w1 = hrany[v][0], w2 = hrany[v][1];
        
        if (oriented.count({w1, v})) {
            if (oriented.count({w2, v}) + oriented.count({v, w2})) {
                DBG cout << "SEEN BOTH NEIGBOURS" << endl;
                return 1; // both were seen
            }
            oriented.insert({v, w2});
            if (!otoc(w2, v, 1, H, parcyc, hrany, oriented)) return 0;
        }
        else if (oriented.count({v, w1})) {
            if (oriented.count({w2, v}) + oriented.count({v, w2})) return 1; // both were seen
            oriented.insert({w2, v});
            if (!otoc(w2, v, 0, H, parcyc, hrany, oriented)) return 0;
        }
        else if (oriented.count({w2, v})) {
            oriented.insert({v, w1});
            if (!otoc(w1, v, 1, H, parcyc, hrany, oriented)) return 0;
        }
        else if (oriented.count({v, w2})) {
            oriented.insert({w1, v});
            if (!otoc(w1, v, 0, H, parcyc, hrany, oriented)) return 0;
        }
        else {
            // first seen, must be a 3-cycle
            DBG cout << "FIRST SEEN" << endl;
            oriented.insert({v, w2});
            oriented.insert({w1, v});
            oriented.insert({w1, w2});
            return 1;
        }
    }
    return 1;
    
}

int main() {
    cin.sync_with_stdio(false);
    cout.sync_with_stdio(false);
    int n = get<int>();
    int m = get<int>();
    
    vector<vector<int> > hrany(n);
    FOR(i, m) {
        int a = get<int>() - 1;
        int b = get<int>() - 1;
        hrany[a].push_back(b);
        hrany[b].push_back(a);
    }
    int v0 = 0;
    FOR(i, n) {
        if (hrany[i].size() > 2) {
            v0 = i;
            break;
        }
    }
    
    DBG cout << "v0 = " << v0 << endl;
    
    vector<int> H(n, -1);
    vector<ii> parcyc(n, {-1, -1});
    
    auto res = treeify(v0, -1, 0, H, parcyc, hrany);
    if (!res.second) {
        cout << "nie" << endl;
        return 0;
    }
    
    
    DBG cout << "H: " << H << "parcyc: " << parcyc;
    
    set<ii> oriented;
    if (!otoc(v0, -1, 1, H, parcyc, hrany, oriented)) {
        cout << "nie" << endl;
    }
    else {
        cout << "ano" << endl;
        for (ii e : oriented) cout << e.first + 1 << " " << e.second + 1 << endl;
    }
    
    
    
}

Diskusia

Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.

Pre pridávanie komentárov sa musíš prihlásiť.

7. Otoč sa! vzorové riešenie