V blízkej budúcnosti krajiny v rámci boja s globálnym otepľovaním zvýšili investície do hromadnej dopravy metrom (lebo je úspornejšia a hlavne v tomto teple pod zemou), a do jadrovej energie (lebo emisie).
Akonáhle všetky jadrové elektrárne povybuchovali, metro sa stalo najväčším centrom civilizácie1. Obyvatelia metra však rýchlo objavili závažný problém – nie všetky tunely metra sú dostatočne hlboko pod zemou, aby cesta nimi bola zabezpečená voči radiácií z povrchu. Toto komplikuje cestovanie z jednej stanice metra do druhej, keďže priamy spoj môže byť viac zdraviu škodlivý ako ísť okľukou. Čo už, zabiť hodinu neoptimálnou trasou je lepšie ako zabiť seba otrávením radiáciou.
Artyom dostal o každom tuneli hlásenie o nameranej radiácií, a veľa dotazov od obyvateľov o najbezpečnejšej trase medzi dvoma stanicami metra. Radšej by však išiel s kamošmi loviť zmutované potkany ako sa prehrabávať mapami a radiť susedom ako najbezpečnejšie odniesť prádlo do práčovne. Poprosil vás preto o pomoc.
Úloha
Trasa medzi dvoma stanicami metra je postupnosť staníc taká, že prvá stanica je začiatočná, posledná je konečná, a každá za sebou idúca dvojica staníc je spojená tunelom.
Nebezpečnosť cesty je najvyššie meranie radiácie v niektorom z tunelov, ktorý je na trase použitý.
Pre každú danú začiatočnú a konečnú stanicu metra nájdite najmenej nebezpečnú trasu medzi nimi, a vypíšte jej nebezpečnosť.
Formát vstupu
V prvom riadku sú čísla \(n\) a \(m\) – počet staníc metra a počet tunelov. V nasledujúcich \(m\) riadkoch sú trojice čísel \(a_i\ b_i\ c_i\), znázorňujúce tunel medzi stanicami \(a_i\) a \(b_i\) s výškou radiácie \(c_i\). Stanice sú očíslované od \(1\) po \(n\), a je zaručené že z každej stanice sa dá dostať do každej inej nejakou postupnosťou tunelov.
Za nimi sa nachádza číslo \(q\) – počet dotazov. Každé z daľsích \(q\) riadkov obsahuje dve čísla \(z_i\ k_i\), dotaz na najbezpečnejšiu cestu začínajúc na stanici \(z_i\) a končiacou stanicou \(k_i\).
Vo všetkých vstupoch platí \(1 \leq n,q\) (aspoň niečo budete mať robiť), \(n-1 \leq m \leq \frac{n(n-1)}{2}\) (ciest je dosť na prepojenie metra, ale nie viac ako možný počet priamych spojení), \(a_i \neq b_i\) (tunel nevedie zo stanice naspäť na ňu) \(1 \leq c_i \leq 10^9\).
| Sada | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(n\) | \(15\) | \(2\,033\) | \(100\,000\) | \(300\,000\) |
| \(m\) | \(15\) | \(2\,033\) | \(100\,000\) | \(300\,000\) |
| \(q\) | \(15\) | \(50\,000\) | \(100\,000\) | \(300\,000\) |
Formát výstupu
Pre každý dotaz vypíšte najmenšie číslo \(0 \leq r_i\) také, že sa dá dostať zo stanice \(z_i\) do \(k_i\) a pritom nepoužiť tunel s radiáciou vyššou ako \(r_i\).
Príklad
Input:
5 5
1 2 5
3 1 10
2 3 6
3 4 9
4 5 3
5
3 1
3 4
3 5
4 5
5 5
Output:
6
9
9
3
0
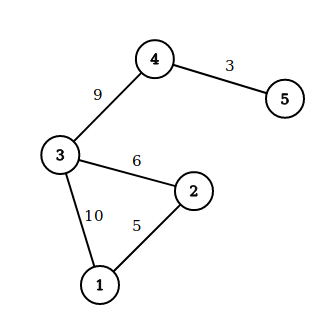
Takto vyzerá sieť metra z príkladu. V prvom dotaze sa nám oplatí ísť okľukou cez stanicu 2.
nemalo na povrchu príliš konkurenciu↩
Odovzdávanie
Na odovzdávanie sa musíš prihlásiť
Otázky a diskusia
Po skončení kola budete mať príležitosť na diskutovanie o riešeniach v diskusii pod vzorovým riešením.