7. Ideálne cestovanie metrom (vzorové riešenie) - Korešpondenčný seminár z programovania

Zadanie

V blízkej budúcnosti krajiny v rámci boja s globálnym otepľovaním zvýšili investície do hromadnej dopravy metrom (lebo je úspornejšia a hlavne v tomto teple pod zemou), a do jadrovej energie (lebo emisie).

Akonáhle všetky jadrové elektrárne povybuchovali, metro sa stalo najväčším centrom civilizácie¹. Obyvatelia metra však rýchlo objavili závažný problém – nie všetky tunely metra sú dostatočne hlboko pod zemou, aby cesta nimi bola zabezpečená voči radiácií z povrchu. Toto komplikuje cestovanie z jednej stanice metra do druhej, keďže priamy spoj môže byť viac zdraviu škodlivý ako ísť okľukou. Čo už, zabiť hodinu neoptimálnou trasou je lepšie ako zabiť seba otrávením radiáciou.

Artyom dostal o každom tuneli hlásenie o nameranej radiácií, a veľa dotazov od obyvateľov o najbezpečnejšej trase medzi dvoma stanicami metra. Radšej by však išiel s kamošmi loviť zmutované potkany ako sa prehrabávať mapami a radiť susedom ako najbezpečnejšie odniesť prádlo do práčovne. Poprosil vás preto o pomoc.

Úloha

Trasa medzi dvoma stanicami metra je postupnosť staníc taká, že prvá stanica je začiatočná, posledná je konečná, a každá za sebou idúca dvojica staníc je spojená tunelom.

Nebezpečnosť cesty je najvyššie meranie radiácie v niektorom z tunelov, ktorý je na trase použitý.

Pre každú danú začiatočnú a konečnú stanicu metra nájdite najmenej nebezpečnú trasu medzi nimi, a vypíšte jej nebezpečnosť.

Formát vstupu

V prvom riadku sú čísla $n$ a $m$ – počet staníc metra a počet tunelov. V nasledujúcich $m$ riadkoch sú trojice čísel $a_i\ b_i\ c_i$, znázorňujúce tunel medzi stanicami $a_i$ a $b_i$ s výškou radiácie $c_i$. Stanice sú očíslované od $1$ po $n$, a je zaručené že z každej stanice sa dá dostať do každej inej nejakou postupnosťou tunelov.

Za nimi sa nachádza číslo $q$ – počet dotazov. Každé z daľsích $q$ riadkov obsahuje dve čísla $z_i\ k_i$, dotaz na najbezpečnejšiu cestu začínajúc na stanici $z_i$ a končiacou stanicou $k_i$.

Vo všetkých vstupoch platí $1 \leq n,q$ (aspoň niečo budete mať robiť), $n-1 \leq m \leq \frac{n(n-1)}{2}$ (ciest je dosť na prepojenie metra, ale nie viac ako možný počet priamych spojení), $a_i \neq b_i$ (tunel nevedie zo stanice naspäť na ňu) $1 \leq c_i \leq 10^9$.

Sada	1	2	3	4
$n$	$15$	$2\,033$	$100\,000$	$300\,000$
$m$	$15$	$2\,033$	$100\,000$	$300\,000$
$q$	$15$	$50\,000$	$100\,000$	$300\,000$

Formát výstupu

Pre každý dotaz vypíšte najmenšie číslo $0 \leq r_i$ také, že sa dá dostať zo stanice $z_i$ do $k_i$ a pritom nepoužiť tunel s radiáciou vyššou ako $r_i$.

Príklad

Input:

Output:

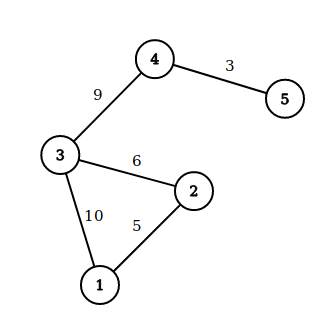
Takto vyzerá sieť metra z príkladu. V prvom dotaze sa nám oplatí ísť okľukou cez stanicu 2.

nemalo na povrchu príliš konkurenciu↩

Krátka rekapitulácia úlohy: Máme ovahovaný graf – $n$ staníc metra prepojených $m$ tunelmi rôznej nebezpečnosti – a $q$ otázok na dve stanice, odpoveďou je také číslo $r$, že nevieme precestovať medzi týmito dvoma stanicami bez toho, aby sme použili tunel s nebezpečnosťou aspoň $r$.

Hrubá sila

V prvej sade máme všetkého – staníc, tunelov, otázok – najviac $15$. Môžeme si teda dovoliť skoro hocičo. Napríklad si môźeme pre každú otázku vyskúšať všetky podmnožiny tunelov, overiť či sa vieme dostať medzi dvoma stanicami z otázky, a ak áno, pozrieť aký najnebezpečnejší tunel sme v podmnožine nechali. Odpovedáme najmenšiou nebezpečnosťou s ktorou sa nám to niekedy podarí. Takéto niečo by zbehlo v $O(q \cdot (n+m)2^n)$.

Jediná správna cesta

Predstavte si, že začíname s metrom v ktorom niesu vybudované žiadne tunely, a teda sa medzi žiadnymi rôznymi stanicami nevieme dostať. Začneme teraz budovať všetky tunely od najmenej nebezpečnejšieho po najnebezpečnejší. Vždy keď ideme stavať tunel, pozrieme sa či už sa medzi danými dvoma stanicami vieme nejako dostať, a ak áno, nepostavíme ho. V istom bode prepojíme celé metro, čiže sa vieme dostať medzi všetkými dvojicami staníc, a žiadny z nevystavaných tunelov by sme ajtak nepoužili – každý z nich je nebezpečnejší ako nejaká množina tunelov, ktoré nám dovoľujú sa pohybovať medzi tými stanicami ktoré tento nebezpečný tunel spája. Získame jednoducho najlacnejšiu kostru mesta, ktorá má stromovú štruktúru.

Najmenej nebezpečná cesta medzi dvoma stanicami $a$ a $b$ je potom presné tá jediná cesta v našej vystavanej kostre, ktorá medzi nimi vedie. Jediné čo potrebujeme zistiť je najdrahšia hrana, ktorá na nej leží.

Túto informáciu si môžeme predpočítať – keď dostaviame kostru, spustíme v cykle s každej stanice prehľadávanie do šírky, v ktorom si navyše pamätáme akú najnebezpečnejšiu hranu sme dosiaľ použili, aby sme sa dostali na danú stanicu. Vždy keď použijeme tunel, túto hodnotu prepíšeme na maximum z nej, a nebezpečnosti tohoto tunela, a túto hodnotu si zapíšeme do tabuľky. Keď nám prehľadávanie do širky skončí, máme $n \times n$ tabuľku, v ktorej na indexe [a][b] máme zapísanú najdrahší tunel, ktorý bol prehľadávaním použitý na cesta z $a$ do $b$.

Každú otázku potom jednoducho odpovedáme v konštantnom čase.

Pamäťová zložitosť našeho riešenia je $O(n^2)$ a časová zložitosť je $O(m \log n)$ na postavanie najlacnejšej kostry, $O(n^2) na prehľadávania do šírky a $O(q)$ na odpovedanie otázok. Dokopy teda $O(n^2+q)$, keďže $m ~ n$.

Ak sa cítime trochu lenivejšie, môžeme namiesto stavania najlacnejšej kostry rovno pustiť prehľadávanie dijkstrou, v ktorej preferujeme vrcholy ktoré sme dosiahli s najmenšou nebezpečnosťou, čo nám síce o logaritmus zhorší zložitosť, ale v druhej sade prejde.

Zdrojové kódy budú zverejnené až po 19.8. 23:59:59. Dovtedy sa môžete pokúsiť úlohu naprogramovať sami
(a získať tým nejaké body navyše).

A však máme strom

Keďže najlacnejšia kostra nášho metra je nutne strom, môžeme siahnuť po nejakom algoritme ktorý na stromoch vieme púšťať. Každá otázka požaduje zistiť informáciu o nejakej ceste v našom strome – najnebezpečnejšiu hranu na nej. Táto informácia má dobrú vlastnosť, že keď máme dve cesty ktoré sa napájajú (cesta z $a$ do $b$ a z $b$ do $c$) a pre ktoré vieme odpoveď, a spojíme ich do jednej cesty ($a$ do $c$), tak pre ňu vieme ľahko spočítať odpoveď – je to maximum z odpovedí pre jednotlivé cesty.

Algoritmus ktorý takéto niečo spokojne zráta je LCA – najnižší spoločný predok. Ak tento algoritmus neovládate, určite si o ňom prečítajte, zvyšok vzoráku ho len priamočiaro použije. Zakoreníme si našu najlacnejšiu kostru o ľubovoľný vrchol, a pri predrátavaní si predkov si rátame aj najnebezpečnejšiu hranu v každom jednotlivom skoku.

Keď dostaneme dotaz na cestu medzi stanicami $a$ a $b$, poskáčeme našimi skokmi mocnín dvojky k ich najnižšiemu spoločnému predkovi, čo teda predstavuje niekoľko ciest ktoré sa dokopy napoja na práve tú jedinú cestu medzi nimi v našom strome, a naša odpoveď je najväčšie číslo ktoré v týchto skokoch stretneme. Každý teda odpovieme v logaritmickom čase.

Pamäťová zložitosť je $O(n \log n)$ na logaritmický počet skokov z každej stanice.

Postaviť kostru nám trvá $O(m \log n)$, predrátať skoky na predkov $O(n \log n)$, a odpovedať na všetky dotazy $O(q \log n)$, celkovo teda $O((m+n+q) \log n)$.

Zdrojové kódy budú zverejnené až po 19.8. 23:59:59. Dovtedy sa môžete pokúsiť úlohu naprogramovať sami
(a získať tým nejaké body navyše).

Diskusia

Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.

Pre pridávanie komentárov sa musíš prihlásiť.

Sada	1	2	3	4
\(n\)	\(15\)	\(2\,033\)	\(100\,000\)	\(300\,000\)
\(m\)	\(15\)	\(2\,033\)	\(100\,000\)	\(300\,000\)
\(q\)	\(15\)	\(50\,000\)	\(100\,000\)	\(300\,000\)

7. Ideálne cestovanie metrom vzorové riešenie