8. Svinstvo na koberci vzorové riešenie

Zadanie

Krtko si na oslavu svojho novo zrekonštruovaného bytu pozval všetkých vedúcich. Kubíkovi sa byt tak páčil, že sa rozhodol kúpiť nový nábytok do Klubovne Spokojných Programátorov. Zohnal nové staré stoly, kolieskové stoličky bez koliesok aj pekné preplnené skrine. Nákup zavŕšil novým viacdielnym kobercom. Ten sa skladá z viacerých kúskov uložených tak, že na podlahe tvoria mapu.

Netrvalo dlho a na čistučkom koberci sa začali každý deň objavovať zablatené stopy, zadupaná čokoláda či škrny od kofoly. Tie treba rýchlo odstrániť, inak sa do koberca zažerú nastálo.

Kubík dostal briliantný nápad. Na strop pripevnil kameru namierenú na koberec, takže vie presnú polohu každej škvrny v momente, keď sa objaví. Od vás chce program, ktorý mu povie veľkosť zašpineného kusu koberca, aby mohol objednať správne množstvo čistiacich prostriedkov.

Úloha

Na vstupe dostanete zadanú mapu koberca v podobe súvislého planárneho grafu (vrcholy so súradnicami a hrany medzi nimi) a niekoľko bodov. Vašou úlohou je pre každý bod nájsť veľkosť uzavretej oblasti, v ktorej leží (tj. jej obsah). Ak sa bod nenachádza v žiadnej uzavretej oblasti, vypíšte \(-1\). Body ležiace na niektorej hrane grafu (vrátane jej okrajov) považujeme, že nie sú vo vnútri žiadnej uzavretej oblasti.

Pozor! Túto úlohu je treba riešiť online, čiže testovač vášmu programu posiela otázky postupne. Každú nasledujúcu otázku dostanete až po tom, čo zodpoviete aktuálnu. Nezabudnite flushovat, aby sa vaša odpoveď skutočne testovaču odoslala a netrávila prázdniny v nejakom buffri. (C++ cout.flush(), Python sys.stdout.flush(), pre iné jazyky si vyhľadajte.)

Formát vstupu

Na prvom riadku vstupu je číslo \(n\)—počet vrcholov, \(m\)—počet hrán a \(q\)—počet otázok.

Potom prázdny riadok, a nasleduje \(n\) riadkov (\(n \geq 1\)) obsahujúcich \(2\) čísla—súradnice daného vrchola. Môžete predpokladať, že žiadne dve vrcholy nie sú ten istý bod v rovine. Všetky súradnice sú celé čísla, ktoré v absolútnej hodnote neprevýšia \(10^9\).

Potom prázdny riadok, a na ďalších \(m\) riadkoch (\(m \geq 0\)) sú vždy \(2\) čísla—čísla vrcholov, medzi ktorými vedú hrany. Vrcholy číslujeme \(1, 2, \ldots, n\). Môžete predpokladať, že ak niektoré tri vrcholy \(a, b, c\) ležia na jednej priamke v tomto poradí, tak na vstupe nebude hrana \(ac\). Takisto sa žiadna hrana na vstupe nevyskytne viackrát, a žiadne dve hrany sa nekrižujú. Koncové vrcholy každej hrany sú rôzne. Zadaný graf je súvislý.

Potom prázdny riadok, a na každom z posledných \(q\) riadkov (\(q \geq 0\)) sú \(2\) čísla—súradnice bodu z otázky.

Súradnice všetkých bodov sú nezáporné a neprevyšujú \(10^9\).

Formát výstupu

Pre každý bod vypíšte riadok obsahujúci jedno číslo—veľkosť oblasti, v ktorej sa nachádza. Ak bod neleží v žiadnej uzavretej oblasti, vypíšte \(-1\). Pokiaľ je výsledok celočíselný, nevypisujte žiadne desatinné miesta, v opačnom prípade vypíšte jedno desatinné miesto. (Rozmyslite si, že obsah každej z oblastí je nutne celočíselným násobkom \(\frac{1}{2}\).)

Hodnotenie

Obmedzenia v jednotlivých sadách sú nasledovné:

Sada	1	2	3	4	5	6	7	8
\(n \leq\)	\(300\)		\(2\,500\)			\(50\,000\)
\(m \leq\)	\(300\)		\(4\,000\)			\(70\,000\)
\(q \leq\)	\(10\,000\)					\(20\,000\)

Príklady

Input:

5 7 5

10 6
7 10
9 1
0 6
2 0

2 4
5 3
1 3
3 4
5 4
4 1
2 1

8 6
0 3
2 5
7 0
8 1

Output:

-1
-1
25
-1
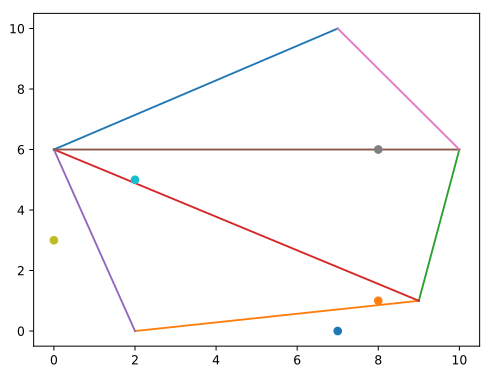
22

Obrázok prvého vstupu:

Input:

7 10 5

7 3
0 4
0 8
3 2
10 0
7 6
0 10

6 2
6 7
5 4
3 7
5 1
6 5
6 4
2 4
3 2
6 3

5 4
5 2
8 1
2 5
4 4

Output:

-1
18
18
14
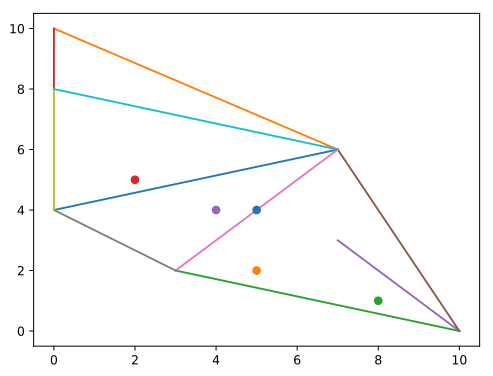
10

Obrázok druhého vstupu:

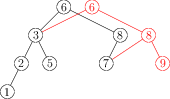
Input:

9 12 5

3 1
4 5
7 0
10 5
8 0
0 6
1 10
5 5
6 5

9 7
8 7
8 2
2 6
4 5
7 2
6 7
3 1
8 9
3 5
3 4
1 8

7 1
3 2
3 7
5 2
9 4

Output:

-1
-1
2.5
-1
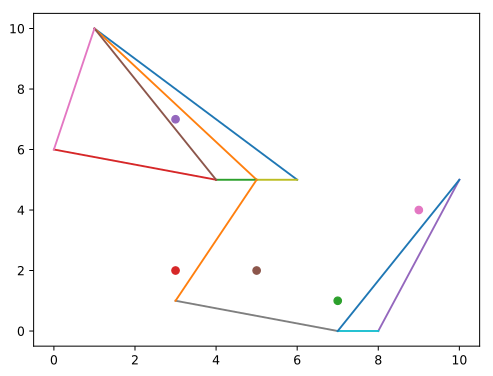
-1

Obrázok tretieho vstupu:

Input:

5 5 5

0 0
0 4
4 4
4 0
1 1

1 2
2 3
3 4
4 1
4 5

1 1
0 4
3 3
0 2
2 4

Output:

-1
-1
16
-1
-1

Obrázok štvrtého vstupu:

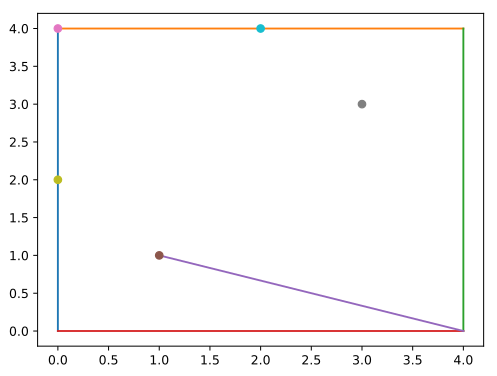
Táto úloha bola fakt ťažká. Dĺžka vzoráku to celkom odzrkadľuje. Nebojte sa teda vzorák spracovávať po kúskoch, kľudne aj vo viacerých sedeniach.

Na získanie \(5\) bodov z programu si stačilo len uvedomiť, čo v skutočnosti znamenajú niektoré geometrické pojmy a ako ich vyjadriť v programe. V geometrii totiž častokrát “vidíme”, že niečo platí, ale nevieme to poriadne zdôvodniť/vyjadriť. Napríklad, čo znamená, že bod \(A\) je vo vnútri nejakej oblasti? Čo to vlastne je oblasť, ako môže vyzerať? Nielen týmito otázkami sa budeme zaoberať v nasledujúcej časti.

Geometria

Základy

Ak ste sa s výpočtovou geometriou ešte nestretli, odporúčame vám najprv prečítať si v našej kuchárke Úvod do výpočtovej geometrie.

Vo vzorovom riešení sa často využívajú skalárny súčin, a obzvlášť vektorový súčin. Ak vám niekde vo vzoráku nebude jasné, ako je niektorý zo súčinov použitý, môžete hľadať odpovede v odpovedajúcom článku v kuchárke: Skalárny a vektorový súčin

Čím je určená oblasť?

Najprv si rozmyslime jednu vec. Naľavo od každej hrany je vždy práve jedna oblasť, a napravo od hrany je vždy práve jedna oblasť. Pritom to môže byť tá istá oblasť, ako naľavo, a obe oblasti môžu byť nekonečné. Je zrejmé, že v oboch smeroch hrana susedí s aspoň jednou oblasť; zároveň vieme prejsť “tesne” popri hrane od jedného konca hrany k druhému, takže oblasť môže byť len jedna.

Tento prechod je umožnený tým, že sa hrany grafu nekrižujú, a že na žiadnej hrane neleží tretí bod. Ak by jedna z týchto podmienok bola porušená, mohlo by na jednej strane hrany byť viacero oblastí. Ilustrujeme na nasledujúcom obrázku:

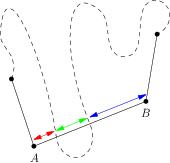
Každá oblasť má teda svoju hranicu, ktorá obsahuje celé hrany. Pretože zadaný graf je súvislý, hranica oblasti musí byť súvislá: ak sú teda nejaké dve hrany na hranici oblasti, vieme sa od jednej hrany dostať k druhej tak, že pôjdeme po okraji. Toto v nesúvislých grafoch nemusí platiť, ako vidno na nasledujúcom obrázku:

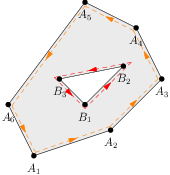
Predstavme si teraz, že ideme po okraji oblasti proti smeru hodinových ručičiek. To samozrejme neznamená, že vždy zatáčame doľava, nakoľko oblasť nemusí byť konvexná. Ako je potom ale definovaný smer “proti smeru hodinových ručičiek”? Je to taký smer, v ktorom je vnútro oblasti vždy na ľavej strane hrany. Môžete si to predstaviť tak, že hranám na okraji oblasti priradíme takú orientáciu, aby bolo vnútro oblasti vždy naľavo od hrany. Samozrejme, sú prípady, kedy je vnútro aj na pravej strane hrany:

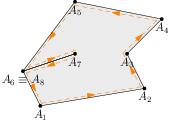
V takom prípade pôjdeme pri našom prechode raz v jednom smere pozdĺž takejto hrany, a raz v druhom smere. Takže tento sled, ktorý “obtiahne” okraj oblasti, môže niektoré hrany obsahovať dvakrát: raz v jednej orientácii a raz v druhej orientácii.

Orientované hrany budeme v ďalšom texte volať šípky. Budeme hovoriť, že šípka patrí tej oblasti, ktorá je naľavo od šípky.

// geometry.cpp

#pragma once

#include <cmath>
using namespace std;

#define INF 1023456789
#define NONE -1
#define EPSILON 0.000000001

typedef long double ld;

bool ld_equals (ld a, ld b) {
  /** Robime s long doublami, treba byt benevolentny pri porovnavani. */
  return abs(a - b) < EPSILON;
}


struct Point {
  /** Bod/vektor v 2D rovine, so standardnymi vektorovymi operaciami. */
  ld x, y;
  
  Point (ld x0, ld y0) : x(x0), y(y0) {}
  
  // Klasicke operacie na vektoroch: sucet, rozdiel, a skalarny nasobok.
  Point operator+ (const Point p) const {
    return Point(x + p.x, y + p.y);
  }
  Point operator- (const Point p) const {
    return Point(x - p.x, y - p.y);
  }
  Point operator* (const ld k) const {
    return Point(k*x, k*y);
  }
  
  // Porovnavanie dvoch vektorov: mensi, vacsi, rovnost, mensi rovny, vacsi rovny.
  bool operator< (const Point p) const {
    /** Porovnavame primarne podla x-ovej, sekundarne podla y-ovej suradnice. */
    return x < p.x || (x == p.x && y < p.y);
  }
  bool operator> (const Point p) const {
    return p < (*this);
  }
  bool operator== (const Point p) const {
    return x == p.x && y == p.y;
  }
  bool operator<= (const Point p) const {
    return !((*this) > p);
  }
  bool operator>= (const Point p) const {
    return !((*this) < p);
  }
  
  ld sp (const Point p) const {
    /** Skalarny sucin tohto vektora s vektorom <p>. */
    return x*p.x + y*p.y;
  }
  ld vp (const Point p) const {
    /** Vektorovy sucin tohto vektora s vektorom <p> (v tomto poradi). */
    return x*p.y - y*p.x;
  }
};

Point operator* (const ld k, const Point p) {
  return p*k;
}


ld comp_time = -INF;    // v ktorom case (x-ovej pozicii) porovnavame?
bool comp_epsilon = 0;  // blizime sa zlava (0) alebo ideme doprava (1)?

struct Edge {
  /** Obsahuje informacie o tom, medzi ktorymi dvomi bodmi ide hrana
   * a aka stena je na lavej a pravej strane. */
  Point from, to;
  int lface, rface;
  
  Edge (Point p, bool epsilon) : from(p), to(p.x + 1, p.y + (epsilon ? INF : -INF)), lface(NONE), rface(NONE)
  {
    /** Ked chceme bod porovnat s hranou, musime to spravit pomocou
     * pomocnej hrany. Na to pouzijeme tento konstruktor, kde <epsilon>
     * hovori, ci sa k suradnici blizime zlava (0), alebo sa od nej
     * vzdalujeme doprava (1). */
  }
  Edge (Point from0, Point to0, int lface0, int rface0)
    : from(from0), to(to0), lface(lface0), rface(rface0) {}
  
  Point to_vector () const {
    return to - from;
  }
  
  bool is_vertical () const {
    return from.x == to.x;
  }
  bool contains (Point p) const {
    /** Lezi bod <p> na tejto hrane? */
    return (p - from).vp(p - to) == 0 && (p - from).sp(p - to) <= 0;
  }
  
  // Porovnavacie operatory.
  bool operator== (const Edge e) const {
    return (from == e.from) && (to == e.to);
  }
  bool operator!= (const Edge e) const {
    return !(*this == e);
  }
  
  ld at (ld x) const {
    /** Vrati y-suradnicu, ktoru hrana nadobuda na danej x-suradnici.
     * Ak je hrana vertikalna, spravi nieco nedefinovane. */
    ld p_from = x - from.x;
    ld p_to = to.x - x;
    ld p_total = to.x - from.x;
    return p_from/p_total * to.y + p_to/p_total * from.y;
  }
};

bool comp (const Edge a, const Edge b) {
  /** Porovna hrany ako vektory ("Je <a> mensi (napravo od) <b>?"). */
  return a.to_vector().vp(b.to_vector()) > 0; // ak je <b> nalavo od <a>
}

bool operator< (const Edge a, const Edge b) {
  /** Porovnanie dvoch hran, na x-ovej suradnici <comp_time>, pricom sa
   * blizime/vzdalujeme podla <comp_epsilon>. */
  ld ay = a.at(comp_time);
  ld by = b.at(comp_time);
  return (ld_equals(ay, by) ? (comp_epsilon ? comp(a, b) : comp(b, a)) : ay < by);
}

bool operator> (const Edge a, const Edge b) {
  return b < a;
}

bool operator<= (const Edge a, const Edge b) {
  return !(b < a);
}

bool operator>= (const Edge a, const Edge b) {
  return b <= a;
}


struct Arrow {
  /** Hrana z pohladu jedneho z jej koncovych bodov. */
  Edge* edge;
  bool reversed;
  
  Arrow (Edge* edge0, bool r0) : edge(edge0), reversed(r0) {}
  
  // Ktory region sa nachadza nalavo/napravo?
  int lface () const {
    return (reversed ? edge->rface : edge->lface);
  }
  int rface () const {
    return (reversed ? edge->lface : edge->rface);
  }
  
  Point from () const {
    return (reversed ? edge->to : edge->from);
  }
  Point to () const {
    return (reversed ? edge->from : edge->to);
  }
  Point to_vector () const {
    return to() - from();
  }
  
  bool operator< (const Arrow other) const {
    return to_vector().vp(other.to_vector()) > 0; // ak som nalavo od other
  }
  bool is_vertical () const {
    return edge->is_vertical();
  }
};

Ktoré šípky sú na okraji?

Predstavme si, že pri obťahovaní okraju sme sa zastavili na nejakej šípke \(A \to B\). Vieme povedať, ktorá šípka bude nasledovať? Zrejme to bude niektorá šípka vychádzajúca z vrcholu \(B\). Ak si nakreslíme všetky šípky vychádzajúce z \(B\), nie je ťažké vidieť, že hľadaná šípka bude \(B \to C\) taká, pri ktorej zatočíme čo najviac doľava:

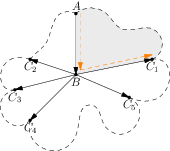
Prečo je toto tá správna šípka? Totiž, vždy vieme ísť tesne popri šípke \(A \to B\) a potom popri \(B \to C\). Pri tomto prechode neprekrížime žiadnu inú šípku, a teda určite patria tieto šipky do tej istej oblasti. Ak by sme skúšali prejsť podobným spôsobom popri iných šípkach vychádzajúcich z vrcholu \(B\), križovali by sme niektorú inú šípku.

Takýmto spôsobom vieme pre každú šípku zistiť celú hranicu oblasti, do ktorej patrí. Pretože každá oblasť má na okraji aspoň jednu šípku, vieme týmto spôsobom získať hranice všetkých oblastí. A pretože šípka je len hrana s priradenou orientáciou, získame týmto pre každú hranu informáciu o tom, ktorá oblasť je na jednej strane a ktorá na druhej strane hrany.

Na celý tento proces sa ale dá pozerať aj iným, prirodzenejším, spôsobom. Pre každú šípku máme dve premenné: číslo oblasti, ktorá je na ľavej strane hrany a číslo oblasti, ktorá je na pravej strane. Pritom pre dvojicu navzájom opačných šípok sú tieto dve premenné iba vymenené – to, čo je naľavo od jednej šípky, je napravo od druhej, a naopak.

Zoberme si teraz všetky šípky vychádzajúce z nejakého bodu \(A\) a usporiadajme si ich polárne (podľa uhlu), proti smeru hodinových ručičiek. Potom pre každú dvojicu po sebe idúcich šípok vieme povedať, že oblasť naľavo od prvej z nich je tá istá, ako oblasť napravo od druhej z nich – teda že sa príslušné premenné rovnajú.

Toto vieme spraviť pre všetky vrcholy, a dostaneme tak sadu rovností nad \(2m\) premennými. Premenné, ktoré sa rovnajú, potom reprezentujú tú istú oblasť. Premenné, ktoré sa nerovnajú, reprezentujú rôzne oblasti. Ak si premenné predstavíme ako vrcholy nejakého grafu a rovnosti ako hrany grafu, tak oblasti zodpovedajú súvislým komponentom tohto grafu.

Dostávame tak jednoduchý algoritmus na výpočet okrajov oblastí, bežiaci v čase \(O(m \log m)\), logaritmus kvôli polárnemu usporiadaniu. Aby sme vedeli šípky polárne usporiadať, potrebujeme vedieť pre dva vektory povedať, ktorý je naľavo od ktorého. To vieme určiť podľa znamienka vektorového súčinu.

Ako vypočítať obsah oblasti?

Ak poznáme hranicu oblasti, vieme aj vypočítať obsah oblasti, nasledovne. Zoberme si ľubovoľný bod v rovine \(S\), napríklad \(S = (0, 0)\). Hranica oblasti zodpovedá nejakému sledu \(A_1 \to A_2 \to \ldots \to A_n \to A_1\), proti smeru hodinových ručičiek. Jednoducho teraz vezmeme orientované obsahy trojuholníkov určených dvojicami vektorov

\[ (\overrightarrow{SA_1}, \overrightarrow{SA_2}), (\overrightarrow{SA_2}, \overrightarrow{SA_3}), \ldots, (\overrightarrow{SA_n}, \overrightarrow{SA_1})\]

a sčítame ich. Tieto orientované obsahy vieme dostať pomocou vektorového súčinu.

Prečo to ale funguje? Zamyslime sa nad najjednoduchším prípadom, keď máme trojuholník \(ABC\). Potom náš výraz je súčtom orientovaných obsahov troch trojuholníkov, jeden pre každú stranu \(\triangle ABC\). Ak je bod \(S\) vo vnútri \(\triangle ABC\), tak jednotlivé podtrojuholníky budú mať všetky kladný obsah, nakoľko \(\overrightarrow{SA_{i + 1}}\) je vždy naľavo od \(\overrightarrow{SA_i}\). Ich súčtom dostaneme celý trojuholník. Ak je bod \(S\) mimo \(\triangle ABC\), tak jeden alebo dva podtrojuholníky budú záporné, a všetko sa to vyruší tak, že zostane iba \(\triangle ABC\).

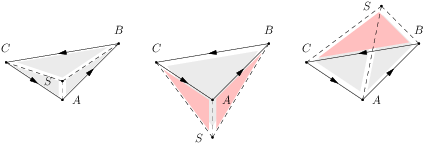
Čo v prípade, keď nemáme trojuholník? Každý (aj nekonvexný) mnohouholník sa dá rozdeliť na niekoľko dizjunktných trojuholníkov (tzv. triangulácia). Na každý z týchto trojuholníkov vieme aplikovať vyššie uvedené tvrdenie, a dostaneme tak obsah nášho mnohouholníka vyjadreného ako súčet niekoľkých orientovaných trojuholníkov. Každý z týchto trojuholníkov má ako jeden z vrcholov \(S\), a ostatné dva vrcholy patria mnohouholníku – teda každý trojuholník zodpovedá buď niektorej hrane v triangulácii (ktorá oddeľuje dva z trojuholníkov), alebo hrane na obvode mnohouholníka.

My chceme ukázať, že v skutočnosti tam budú vystupovať iba hrany z obvodu mnohouholníka. To je ale zrejmé: každá vnútorná hrana susedí s dvomi podtrojuholníkmi: v jednom z nich bude vnútro trojuholníka naľavo od hrany (a zarátame ho s kladným znamienkom), v druhom z nich bude vnútro trojuholníka napravo od hrany (záporné znamienko).

Pozorný čitateľ si isto všimne jeden zvláštny prípad. Čo sa stane, ak tá oblasť, po okraji ktorej ideme, je nekonečná? Zrejme vypočítame obsah útvaru určeného týmto okrajom (tj. obsah toho, čo je “skutočne vnútri”, nie vonku). Aké znamienko ale bude mať takto vypočítaný obsah? Definovali sme “proti smeru hodinových ručičiek” tak, že vnútro oblasti je naľavo od šípky. Nie je ťažké rozmyslieť si, že pre (jedinú) nekonečnú oblasť je takto definovaný sled v skutočnosti v smere hodinových ručičiek:

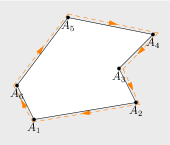
Dostaneme teda záporný alebo nulový obsah. Pomocou znamienka teda vieme určiť, či je bod vo vnútri nekonečnej oblasti, alebo v konečnej.

Časová zložitosť výpočtu obsahu oblasti je \(O(k)\), kde \(k\) je počet vrcholov/hrán na okraji oblasti. Nakoľko každá šípka patrí iba do jednej oblasti, a všetkých šípok je \(2m\), celková časová zložitosť tohto predrátania je \(O(m)\).

Prvé riešenie

Už teda vieme, ako nájsť hranice všetkých oblastí, a tiež ako podľa týchto hraníc vypočítať obsah oblasti. Aby sme ale vedeli odpovedať na otázky, musíme ešte vedieť pre ľubovoľný bod \(X\) povedať, v ktorej oblasti leží, prípadne, že leží na niektorej hrane.

Zistiť, či bod leží na hrane, vieme v čase \(O(m)\): iba postupne prejdeme všetky hrany, a pre každú hranou overíme, či na nej \(X\) leží alebo nie. Ako to ale overíme? Pomocou vektorového súčinu vieme zistiť, či \(X\) leží na priamke určenej touto hranou. Pomocou skalárneho súčinu zistíme, či je \(X\) “vo vnútri” úsečky alebo mimo nej.

Ak neleží na hrane, ako zistíme, do ktorej oblasti patrí? Vieme sa pozrieť na najbližšiu hranu, ktorá je “pod” naším bodom. Hľadaná oblasť je tá, ktorá je “hore” od tejto hrany. Ak žiadna hrana pod bodom \(X\) nie je, tak bod zrejme neleží v žiadnej konečnej oblasti.

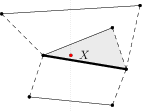
Čo to ale znamená hore? Ak každú (nezvislú) hranu orientujeme tak, že ide zľava doprava (tj. od menších \(x\)-ových súradníc k väčším), tak “hore” znamená “vľavo”. Budeme hovoriť, že ľavý koniec hrany je jej začiatok a pravý koniec hrany je jej koniec.

Potrebujeme teda zistiť, ktoré hrany majú spoločnú \(x\)-ovú súradnicu s naším bodom \(X\). (Ak by sme nakreslili zvislú čiaru cez \(X\), tak sú to tie hrany, ktoré majú s touto čiarou nejaký spoločný bod.) Spomedzi týchto hrán chceme nájsť tú, ktorá pretína zvislú čiaru cez \(X\) čo najvyššie, ale stále pod bodom \(X\). Čo ale v prípade, že takýchto najvyšších hrán je viac? Takýto prípad môže nastať jedine vtedy, ak je bod \(X\) priamo nad niektorým vrcholom. Ako ukazuje nasledujúci obrázok, nie je jedno, ktorú hranu vyhlásime za najvyššiu:

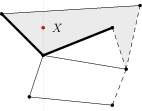
V takom prípade chceme vybrať takú hranu, ktorá v tom vrchole začína (končí) a ktorá ide čo najrýchlejšie hore (dole). Inak povedané, spomedzi všetkých hrán začínajúcich (končiacich) v tomto vrchole chceme vybrať tú najľavejšiu (najpravejšiu). Porovnať dve hrany, že ktorá je vľavo (vpravo) od ktorej, vieme jednoducho pomocou vektorového súčinu.

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

// V riadnych projektoch prosim neincludujte .cpp, ale len header (.hpp)
// subory. Tu pre jednoduchost includujeme .cpp subory.
#include "geometry.cpp"
#include "regions.cpp"
#include "bst.cpp"


#define NONE -1


int main () {
  int n, m, q;
  cin >> n >> m >> q;
  
  vector<Point> P;
  P.reserve(n);
  for (int i = 0; i < n; i++) {
    int x, y;
    cin >> x >> y;
    P.push_back(Point(x, y));
  }
  
  vector<Edge*> E;
  E.reserve(m);
  vector<vector<Arrow> > adj(n);  // adj[i] := sipky vychadzajuce z vrcholu i
  for (int i = 0; i < m; i++) {
    int a, b;
    cin >> a >> b;
    a--; b--;
    if (P[b] < P[a]) {  // hrana vzdy ide od mensieho bodu do vacsieho
      swap(a, b);
    }
    Edge* e = new Edge(P[a], P[b], 2*i, 2*i+1);
    E.push_back(e);
    adj[a].push_back(Arrow(e, 0));
    adj[b].push_back(Arrow(e, 1));
  }
  
  // spocitame si regiony
  vector<vector<Arrow> > borders;
  vector<ld> areas;
  calc_regions(adj, E, borders, areas);
  
  // Zodpovieme otazky!
  for (int quest = 0; quest < q; quest++) {
    int x, y;
    cin >> x >> y;
    Point p(x, y);
    
    // Prejdeme vsetky hrany a overime, ci nas bod lezi na niektorej.
    // Ak ano, odpoved je -1.
    bool contained = false;
    for (Edge* e : E) {
      if (e->contains(p)) {
        contained = true;
        break;
      }
    }
    if (contained) {
      cout << "-1" << endl;
      continue;
    }
    
    // Najdeme najblizsiu hranu ktora je pod nasim bodom, a podla nej
    // cislo regionu nad nou. Podla toho zodpovieme otazku.
    comp_time = x;
    comp_epsilon = 1;
    Edge temp(p, 1);
    Edge* lb = NULL;
    for (Edge* e : E) {
      if (e->to.x <= x || e->from.x > x) { // toto automaticky eliminuje zvisle hrany
        continue;
      }
      if (*e <= temp) {
        if (lb == NULL || *e > *lb) {
          lb = e;
        }
      }
    }
    if (lb == NULL) {
      cout << "-1" << endl;
      continue;
    }
    int face = lb->lface;
    if (areas[face] <= 0) {
      cout << "-1" << endl;
      continue;
    }
    cout << (long long)(areas[face] / 2) << ((long long)areas[face] % 2 ? ".5" : "") << endl;
  }
  
  return 0;
}

Máme tak algoritmus s časovou zložitosťou \(O(m)\) na jednu otázku, celková časová zložitosť je teda \(O(m \log m + mq)\). Toto riešenie si vyslúžilo \(5\) bodov z testovania.

Cesta k lepšiemu riešeniu

Potrebujeme urýchliť dve veci: vedieť rýchlo zistiť, či náš bod \(X\) leží na niektorej hrane; a vedieť rýchlo nájsť najbližšiu hranu pod naším bodom.

Rozdeľme si prácu trochu inak: ak by sme za hrany pod naším bodom považovali aj tie, ktoré cez nehoprechádzajú, stačilo by nám v prvej časti overovať iba zvislé hrany. Ak totiž \(X\) leží na nezvislej hrane, bude to najvyššia hrana pod \(X\). Nezvislé hrany teda vieme vybaviť tak, že pre najvyššiu hranu pod \(X\) overíme, či na nej \(X\) leží alebo nie.

Ako zistiť, či náš bod leží na nejakej zvislej hrane? Jednoducho: spomedzi vrcholov s rovnakou \(x\)-ovou súradnicou nájdeme ten vrchol \(A\), ktorý je najvyššie, ale stále nižšie, ako \(X\). Ak náš bod leží na zvislej hrane, musí to byť zvislá hrana, ktorá vychádza z \(A\) a ide “hore”. Stačí si teda usporiadať všetky vrcholy primárne podľa \(x\)-ovej, sekundárne podľa \(y\)-ovej súradnice, a pre každý vrchol si zapamätať (najviac jednu) šípku hore, ktorá z neho vychádza. V tomto zozname potom binárne vyhľadáme najväčší bod menší rovný \(X\) a overíme, či \(X\) leží na šípke hore alebo nie.

Ako ale rýchlo nájsť tú hranu, ktorá je pod \(X\)? Ak by sme mohli riešiť úlohu offline, teda ak by sme vedeli dopredu všetky otázky, vedeli by sme použiť prístup zvaný zametanie.

Offline zametanie

Ak by sme mali k dispozícii všetky otázky dopredu, mohli by sme sa rozhodnúť ich spracovať v nejakom konkrétnom poradí. Napríklad si môžeme všimnúť, že keď bod \(X\) iba trochu posunieme doprava alebo doľava, množina hrán, ktoré sú pod alebo nad \(X\), sa zmení iba trochu. V probléme je istá lokálnosť. Dobré poradie, v ktorom spracovať otázky, je potom napríklad zľava doprava.

Predstavme si teda, že nekonečne vľavo máme zvislú priamku, tzv. zametaciu čiaru, ktorá sa posúva doprava. Táto čiara nám postupne bude “skenovať” všetky hrany a všetky otázky. Keď čiara narazí na začiatok alebo koniec hrany, upraví svoj stav (tj. ktoré hrany ju pretínajú), a keď čiara narazí na otázku, na základe svojho stavu ju zodpovie.

Konkrétnejšie, keď čiara narazí na ľavý koniec hrany, túto hranu pridá do množiny hrán, s ktorými máme aktuálne priesečník. Keď čiara narazí na pravý koniec hrany, danú hranu z množiny vyhodí. A nakoniec, keď narazí na bod \(X\) reprezentujúci otázku, nájde spomedzi všetkých aktuálnych hrán tú, ktorá má na tejto \(x\)-ovej súradnici priesečník čo najvyššie, ale stále nižšie alebo rovnako vysoko, ako je \(X\).

Zametacia čiara nám teda musí byť schopná povedať, ktorá hrana je na aktuálnej \(x\)-ovej súradnici “tesne pod” bodom \(X\). Tiež musíme vedieť do nej pridávať a odoberať hrany. Vhodnou dátovou štruktúrou na toto je vyvažovaný vyhľadávací strom, v ktorom budeme mať hrany usporiadané podľa ich aktuálnej \(y\)-ovej súradnice (tj. v akej výške pretínajú zametaciu čiaru).

Môžeme si ho ale dovoliť použiť? V našom prípade je totiž výsledok porovnania dvoch hrán závislý od toho, aká je \(x\)-ová pozícia zametacej čiary. Nemôže sa počas posúvania čiary stať, že sa výsledky niektorých porovnaní zmenia, a štruktúra stromu už nebude korektná? Dve hrany zmenia svoje relatívne poradie jedine vtedy, keď sa krížia. To sa ale v našom planárnom grafe nikdy nestane: pred tým, než by k tomu došlo, by jedna alebo obe hrany skončili v niektorom (možno v tom istom) vrchole.

Môže sa ale stať, že dve hrany skončia v jednom a tom istom vrchole; alebo že jedna hrana skončí vo vrchole, v ktorom druhá hrana začne; alebo že obe hrany začnú v tom istom vrchole. V tom momente ich nie sme schopní porovnať, lebo ich priesečníky so zametacou čiarou budú ten istý bod. Pritom ale nie je jedno, ktorú z tých hrán prehlásime za väčšiu a ktorú za menšiu.

Ak totiž dve hrany začínajú v tom istom vrchole, v tom momente ich síce nevieme porovnať, ale hneď v nasledujúcom momente (tj. keď sa zametacia čiara posunie o máličko doprava) ich budeme vedieť porovnať: tá hrana, ktorá rastie rýchlejšie (je viac vľavo), je tá väčšia. Teda pri pridávaní nových hrán ich musíme do stromu dať podľa toho.

Naopak, ak dve hrany končia v tom istom vrchole, v tom momente ich síce nevieme porovnať, ale v predchádzajúcom momente sme ich vedeli porovnať: tá hrana, ktorá klesá rýchlejšie (je viac vpravo), je väčšia. Ak by sme ale toto pri mazaní hrany odignorovali, mohli by sme omylom zmazať tú nesprávnu hranu.

A čo v treťom prípade, keď jedna hrana začína v tom vrchole, v ktorom iná hrana končí? Našťastie sa tomuto prípadu vieme vyhnúť tým, že najprv vybavíme všetky hrany končiace vo vrchole, a až potom všetky hrany začínajúce vo vrchole. Týmto zaručíme, že nikdy nebudeme mať v našom vyhľadávacom strome hranu, ktorá v nejakom vrchole začína spolu s hranou, ktorá v tomto vrchole končí.

Takže naše porovnávanie bude závisieť nielen od toho, aká je momentálna \(x\)-ová súradnica zametacej čiary, ale aj od toho, či sa k nej blížime zľava (vybavujeme konce hrán) alebo sa od nej vzďaľujeme doprava (vybavujeme začiatky hrán). Týmto sme vybavili všetky možné prípady.

Drobný technický detail: vo vyhľadávacom strome vieme porovnávať iba dve hrany, nevieme porovnať bod a hranu. Nebudeme teda porovnávať priamo s bodom \(X\), ale s akousi pomocnou hranou, ktorá bude prechádzať cez \(X\). Aký bude jej sklon? Nemôže byť ľubovoľný: chceme totiž, aby všetky hrany prechádzajúce cez \(X\) boli menšie, aby sme vedeli detekovať, že \(X\) leží na hrane. Takže podľa toho, či sa zľava blížime do \(x\), alebo sa od neho sprava vzďaľujeme, nastavíme sklon hrany na “takmer zvislo hore” alebo “takmer zvislo dole”.

Na začiatku musíme všetky začiatky, konce hrán a otázky utriediť, čo trvá \(O((m + q) \log {(m + q)})\). Samotné zametanie trvá rovnako dlho, nakoľko v každom kroku robíme jednu operáciu s vyvažovaným vyhľadávacím stromom (insert, delete alebo lower_bound), ktorá trvá \(O(\log {(m + q)})\). Celková časová zložitosť je teda \(O((m + q) \log {(m + q)})\).

Toto riešenie si samozrejme vyslúžilo \(0\) bodov, so správou TLE – čakalo totiž na všetky otázky, ktoré mu testovač nebol ochotný dať…

Perzistentný stav čiary

Ak by sme sa vedeli pozrieť na stav zametacej čiary v ľubovoľnom momente, nemuseli by sme všetky otázky zodpovedať od najľavejšej po najpravejšiu. Stačilo by sa pre každú otázku \((x, y)\) pozrieť na stav zametacej čiary v momente \(x\), a podľa neho odpovedať.

Potrebujeme si teda zapamätať celú históriu zametacej čiary a vedieť v nej vyhľadať posledný stav, ktorý predchádzal otázke \(X\). Takýmto “historickým” dátovým štruktúram (ktoré si vedia pamätať nielen ich aktuálny stav, ale aj všetky predchádzajúce) sa hovorí perzistentné dátové štruktúry.

Jedna možnosť je zakaždým, keď chceme zmeniť stav čiary, celý stav skopírovať a vykonať zmenu v kópii. Tieto stavy si potom uložíme do poľa, a pre každý stav si budeme pamätať, v akom časovom momente začal. V tomto poli potom budeme pri otázke \((x, y)\) vedieť binárne vyhľadať poslednú verziu pred (alebo zarovno s) \(x\).

Toto je ale pomalé: pri každej udalosti musíme skopírovať celý strom, čo trvá až \(O(m)\). Udalostí je tiež \(O(m)\), predpočítanie teda bude trvať až \(O(m^2)\), a pamäťová zložitosť bude rovnaká.

My si ukážeme dve prístupy, ktoré dosahujú lepšiu časovú zložitosť: fat nodes a path copying.

Fat nodes

Pri programovaní používame rôzne objekty, a každý objekt si vieme predstaviť ako zoskupenie niekoľkých údajov, nie nutne rovnakých typov. Napríklad vrchol vo vyhľadávacom strome môže obsahovať tieto údaje: ukazovateľ na ľavého syna, pravého syna, a čo je vo vrchole.

Štandardne, keď zmeníme jeden z týchto údajov na iný, stratíme pôvodnú hodnotu. Nevieme ale zmeny údajov spracovať iným spôsobom, tak, aby sa nám zachovala aj pôvodná informácia? Vieme. Budeme si pamätať všetky doterajšie verzie údaju, a pre každú verziu aj čas, kedy táto verzia vznikla (tj. kedy nahradila starú verziu). Keď teraz chceme pristúpiť k údaju v (diskrétnom) čase \(t\), iba binárne vyhľadáme, akú hodnotu v tom čase mal, a vrátime ju. Toto spôsobí iba mierne spomalenie: konkrétne, všetko bude \(O(\log t)\)-krát pomalšie, kde \(t\) je počet verzii údaju. Pamäť bude ale až \(O(t)\) namiesto \(O(1)\).

Ak náš vyhľadávací strom implementujeme týmto spôsobom, dostaneme perzistentný vyhľadávací strom. Samozrejme, potrebujeme vyvažovaný vyhľadávací strom, napríklad treap.

Otázka je, o koľko pomalší bude oproti pôvodnému stromu. Udalostí (začiatok alebo koniec hrany) je \(O(m)\). Pri každej udalosti sa zmení nanajvýš \(O(\log m)\) vrcholov stromu, a “narazíme” pri binárnom vyhľadávaní nanajvýš na všetky doterajšie zmeny. Pred \(i\)-tou udalosťou bolo týchto zmien \(O(i \log m)\), na jeden vrchol teda pripadá spomalenie \(O(\log \frac{i \log m}{\log m}) = O(\log i)\).

Spomalenie jednej operácie je teda \(O(\log m)\) a časová zložitosť predpočítania teda bude \(O(m \log^2 m)\). Podobne, zodpovedanie jednej otázky bude o \(O(\log m)\) pomalšie, a teda dokopy \(O(q \log^2 m)\). Pamäťová zložitosť bude \(O(m \log m)\), nakoľko každá zmena prispeje \(1\).

Path copying

Predstavme si, že objekty, ktoré už existujú, nevieme meniť. Jediné, čo vieme robiť, je vytvárať zo starších objektov nové. Takémuto prístupu k programovaniu sa hovorí aj funkcionálne programovanie.

Načo také niečo je? Dá sa takto vôbec programovať? Ako to súvisí s perzistentnými dátovými štruktúrami? Hneď uvidíme.

Predstavme si, že chceme funkciu, ktorá zmení stav nejakého objektu. Napríklad vezme ako vstup zoznam čísel a na jeho koniec pridá číslo \(4\). Nevieme to spraviť priamo, nakoľko nevieme zmeniť stav vstupného zoznamu. Vieme ale spraviť funkciu, ktorá nám vráti nový zoznam, ktorý bude reprezentovať nový stav vstupného zoznamu. Napríklad ak vstupom je \(a = [1, 2, 3]\), výstupom bude nejaké \(b = [1, 2, 3, 4]\). Zoznam \(a\) ale stále obsahuje pôvodné údaje.

No a tu si môžeme uvedomiť, že čo sa v podstate stalo je, že sme síce dostali novú verziu objektu, ale máme aj starú verziu objektu. Ak by sme týmto prístupom implementovali náš vyhľadávací strom, dostali by sme perzistentný vyhľadávací strom.

Presnejšie, každý vrchol stromu reprezentuje vyhľadávací storm zodpovedajúci podstromu tohto vrcholu. Každá operácia, ktorá mení stav podstromu (insert, delete a rotácie) nám strom nezmení, ale vráti nový vrchol reprezentujúci nový stav (pod)stromu. Tieto operácie sú z veľkej časti definované pomocou operácii na synoch.

Ilustrujeme operáciu insert na nevyvažovanom vyhľadávacom strome nad číslami. Keď chceme vložiť číslo \(5\) do koreňa, chceme ho vložiť do ľavého syna, lebo \(5\) je menšie ako číslo v koreni. Takže výsledkom insertu bude niečo ako strom(lavy_syn->insert(5), hodnota_v_koreni, pravy_syn), kde strom je konštruktor (vytvorí nový strom s daným ľavým synom, danou hodnotou v koreni, a s daným pravým synom). To isté sa potom udeje aj v ľavom synovi, …, až kým nedôjdeme do listu. Dostaneme tak \(O(h)\) nových vrcholov, kde \(h\) je hĺbka stromu.

Prístup sa volá path copying podľa toho, že v podstate pri každej zmene skopírujeme celú cestu od listu až ku koreňu, a kópiu upravíme. Samozrejme, pre efektívnosť potrebujeme strom vyvažovať, my sme (opäť) zvolili treap.

Aká je časová a pamäťová zložitosť? Vždy, keď sa v najaktuálnejšej verzii stromu zmení nejaký vrchol, musíme zmeniť (skopírovať) aj všetkých jeho predkov. Pri každej operácii v štandardnom treape sa zmení vždy nanajvýš \(O(\log m)\) vrcholov, z tohto by plynul (časový aj pamäťový) odhad \(O(\log^2 m)\) na jednu operáciu. Avšak ukazuje sa, že všetky tieto zmeny v treape sú “zarovnané”, tj. že väčšinou sa mení iba jeden vrchol a jeho predkovia. Z toho vyplynie lepší odhad \(O(\log m)\).

Časová zložitosť predpočítania teda bude \(O(m \log m)\), pamäťová zložitosť bude rovnaká. Zodpovedanie otázok bude trvať \(O(q \log m)\). Toto je lepšie, ako v prístupe fat nodes.

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

// V riadnych projektoch prosim neincludujte .cpp, ale len header (.hpp)
// subory. Tu pre jednoduchost includujeme .cpp subory.
#include "geometry.cpp"
#include "regions.cpp"
#include "bst.cpp"


int main () {
  int n, m, q;
  cin >> n >> m >> q;
  
  vector<Point> P;
  P.reserve(n);
  for (int i = 0; i < n; i++) {
    int x, y;
    cin >> x >> y;
    P.push_back(Point(x, y));
  }
  
  vector<Edge*> E;
  E.reserve(m);
  vector<vector<Arrow> > adj(n);  // adj[i] := sipky vychadzajuce z vrcholu i
  vector<Edge*> vertical(n);      // vertical[i] := hrana vychadzajuca z i iduca hore,
                                  //                alebo NULL ak taka nie je
  for (int i = 0; i < m; i++) {
    int a, b;
    cin >> a >> b;
    a--; b--;
    if (P[b] < P[a]) {  // hrana vzdy ide od mensieho bodu do vacsieho
      swap(a, b);
    }
    Edge* e = new Edge(P[a], P[b], 2*i, 2*i+1);
    E.push_back(e);
    adj[a].push_back(Arrow(e, 0));
    adj[b].push_back(Arrow(e, 1));
    if (P[a].x == P[b].x) { // nastavime, ze <e> je vertikalna hrana z <a> hore
      vertical[a] = e;
    }
  }
  
  // spocitame si regiony
  vector<vector<Arrow> > borders;
  vector<ld> areas;
  calc_regions(adj, E, borders, areas);
  
  // Usporiadame si vrcholy od najmensieho po najvacsi, aby sme
  // potom vedeli binarne vyhladat najvacsi mensi alebo rovny bod.
  vector<int> pOrder(n);                  // pOrder[i] := ktory bod je i-ty?
  vector<pair<Point, int> > sortedP;
  sortedP.reserve(n);
  for (int i = 0; i < n; i++) {
    sortedP.push_back({P[i], i});
  }
  sort(sortedP.begin(), sortedP.end());
  for (int i = 0; i < n; i++) {
    pOrder[i] = sortedP[i].second;
  }
  
  // Zametanie, s perzistentnym stavom.
  vector<Treap<Edge>*> H;
  Treap<Edge>* curr = new Treap<Edge>();
  H.reserve(n+1);
  H.push_back(curr);
  for (int i : pOrder) {
    comp_time = P[i].x;
    comp_epsilon = 0;
    for (Arrow a : adj[i]) {
      if (a.is_vertical() || !a.reversed) { // zvisle hrany a hrany iduce doprava ignorujeme
        continue;
      }
      curr = curr->remove(a.edge);
    }
    comp_epsilon = 1;
    for (Arrow a : adj[i]) { // zvisle hrany a hrany vchadzajuce zlava ignorujeme
      if (a.is_vertical() || a.reversed) {
        continue;
      }
      curr = curr->insert(a.edge);
    }
    H.push_back(curr);
  }
  
  // Zodpovieme vsetky otazky!
  for (int quest = 0; quest < q; quest++) {
    int x, y;
    cin >> x >> y;
    Point p(x, y);
    
    { // Najprv zistime, ci bod lezi na niektorej zvislej hrane.
      // Na to najprv vyhladame najvacsi mensi alebo rovny bod.
      int l = -1, r = n;
      while (r-l > 1) {
        int s = (l+r) / 2;
        Point midp = P[pOrder[s]];
        if (p >= midp) {
          l = s;
        }
        else {
          r = s;
        }
      }
      // Ak existuje mensi alebo rovny bod: ak je to rovny bod, rovno
      // balime. Inak sa pozrieme sa na hranu iducu z neho hore. Lezi
      // nas bod na tejto hrane?
      if (l >= 0) {
        int i = pOrder[l];
        Point start = P[i];
        Edge* up = vertical[i];
        if (start == p || (up != NULL && up->contains(p))) {
          cout << "-1" << endl;
          continue;
        }
      }
    }
    
    // Vyhladame spravnu verziu treapu (poslednu, co bola pred alebo
    // zarovno s nasim bodom).
    int l = -1, r = n;
    while (r-l > 1) {
      int s = (l+r) / 2;
      Point midp = P[pOrder[s]];
      if (p >= midp) {
        l = s;
      }
      else {
        r = s;
      }
    }
    
    // V tejto verzii treapu najdeme lower_bound (najvacsiu hranu,
    // ktora je mensia alebo rovna ako nas bod). Podla tejto hrany
    // zodpovieme otazku.
    comp_time = x;
    comp_epsilon = 1;
    Edge temp(p, 1);
    Treap<Edge>* node = H[r]->lower_bound(&temp);
    if (node == NULL || node->value->contains(p)) {
      cout << "-1" << endl;
      continue;
    }
    int face = node->value->lface;
    if (areas[face] <= 0) {
      cout << "-1" << endl;
      continue;
    }
    cout << (long long)(areas[face] / 2) << ((long long)areas[face] % 2 ? ".5" : "") << endl;
  }
  
  return 0;
}

Záverečné poznámky

Dátovým štruktúram, ktorých stav sa nemení (ang. immutable) a vedia iba vracať nové objekty, sa hovorí funkcionálne dátové štruktúry. Ich výhodou oproti iným implementáciám perzistencie je, že sme schopní “pokračovať” nielen v aktuálnej verzii objektu, ale aj v starých verziách. Časová os teda nemusí byť os, môže to byť aj strom.

Naproti tomu ale existuje implementácia perzistentného treapu, ktorá potrebuje menej pamäte: iba \(O(1)\) amortizovane na každú zmenu, oproti \(O(\log m)\) v prípade funkcionálneho treapu. Pre záujemcov odporučím tento článok od legiend Sleatora a Tarjana, strany \(93\) až \(97\).