Úvod do výpočtovej geometrie

Úvod: dvojrozmerný priestor

Dvojrozmerný priestor si vieme predstaviť ako štvorcovú sieť so súradnicovou sústavou. Vodorovnú os označujeme $x$, zvislú $y$. Miesto, kde sa osi $x$ a $y$ pretínajú nazývame počiatok súradnicovej sústavy. Aby sme vedeli číslami popísať, kde sa čo nachádza, používame súradnicový systém -- osi si rozdelíme na rovnako veľké dieliky, ktoré označíme číslami. (V ďalších obrázkoch čísla vynecháme, aby obrázky neboli prepchaté.)

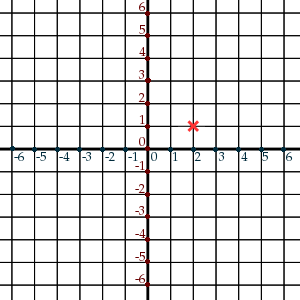
V dvojrozmernom priestore sa môžu vyskytovať rôzne objekty. Najjednoduchším takým objektom je bod, ktorý je určený svojou polohou. Na prvom obrázku máme bod označený krížikom, ktorý sa nachádza na súradniciach $(2, 1)$ (dva kroky doprava a jeden krok hore od počiatku súradnicovej sústavy). Na druhom obrázku sme pridali tri ďalšie body -- zelený na súradnice $(0, 4)$, modrý na súradnice $(-4, 3)$ a oranžový na súradnice $(-2, -5)$.

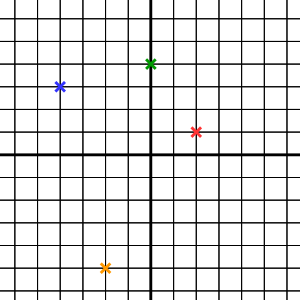
Ďalším objektom je vektor. Vieme si ho predstaviť ako šípku v súradnicovej sústave, ktorá má nejakú dĺžku a nejaký smer. Vektory sa zvyknú, rovnako ako body, označovať dvojicou čísel. V prípade vektorov táto dvojica čísel hovorí o tom, o koľko je vzdialený koniec vektora v smere $x$-ovej a $y$-ovej súradnice od jeho začiatku. Na obrázku je tmavočervenou nakreslený vektor, ktorý vieme zapísať ako $(2, 1)$. Všimnite si, že je to rovnaká dvojica čísel, ako pri červenom bode -- je to kvôli tomu, že tento vektor je vlastne šípkou z počiatku súradnicovej sústavy do červeného bodu.

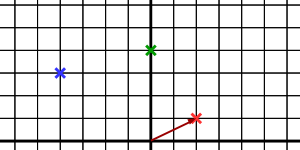
Na ďalšom obrázku vidíme dve fialové šípky. Vektory, ktoré im zodpovedajú, označujeme $(-4, -1)$ a $(-4, -1)$. Prečo ich označujeme rovnako? Ide totiž o ten istý vektor, ktorý je nakreslený dvakrát. Zo zápisu vektora sa nedá určiť, kde v súradnicovej sústave sa nachádza, iba to, o koľko sa ním posunieme.

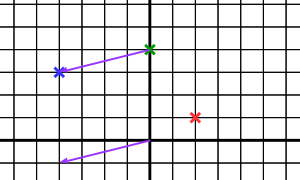
Vektory a body môžeme sčítavať a odčítavať. Obe operácie robíme po jednotlivých súradniciach (čiže prvú súradnicu sčítame s prvou, druhú s druhou). Sčítaním bodu a vektora dostaneme bod -- napríklad sčítaním zeleného bodu a fialového vektora dostaneme modrý bod ($(0, 4) + (-4, -1) = (-4, 3)$). Pričítanie vektora k bodu vlastne predstavuje "presun" z daného bodu do výsledného. Sčítaním dvoch vektorov dostaneme vektor (taký, ktorý nás z ľubovoľného bodu $X$ posunie do takého bodu $Y$, do akého by sme sa dostali, ak by sme ku $X$ pripočítali najprv prvý a k výsledku potom druhý vektor) -- napríklad sčítaním fialového a červeného vektora vznikne vektor $(-2, 0)$ (čiže $(-4, -1) + (2, 1) = (-2, 0)$). Rozdielom dvoch vektorov je opäť vektor (odčítanie vektora si vieme predstaviť ako pohyb pozdĺž vektora v opačnom smere) -- napríklad keď odčítame od červeného vektora fialový, dostaneme vektor $(6, 2)$ (čiže $(2, 1) - (-4, -1) = (6, 2)$). Rozdielom dvoch bodov je tiež vektor (ten, ktorým sa posunieme z druhého bodu do prvého) -- napriklad odpočítaním zeleného bodu od modrého dostaneme fialový vektor ($(-4, 3) - (0, 4) = (-4, -1)$).

Body, vektory a skaláry vo všeobecnosti

Keď sme sa už zoznámili s bodmi a vektormi v dvojrozmernom priestore, môžeme sa pustiť aj do vyšších rozmerov (dimenzií). Trojrozmernú súradnicovú sústavu si vieme predstaviť ako priestor so šírkou, výškou a hĺbkou. Štvor- a viacrozmerné sústavy sa predstavujú ťažšie, ale so zápisom bodov a vektorov v nich sa pracuje rovnako ako pri dvoj- alebo trojrozmernej sústave.

Bod v $n$-rozmernom priestore reprezentujeme ako $n$-ticu čísel $X = (x_1, \dots, x_n)$. Vektor v $n$-rozmernom priestore reprezentujeme tiež ako $n$-ticu čísel $A = (a_1, \dots, a_n)$. Ako sme si povedali už vyššie, vieme si ho predstaviť ako šípku, ktorá nás posunie z bodu $X$ do bodu $(x_1 + a_1, \dots, x_n + a_n) = X + A$. Vektory a body môžeme sčítavať a odčítavať presne tak, ako v dvoch rozmeroch -- po súradniciach. (Napríklad pri sčítavaní postupujeme presne tak, ako je napísané pre $X + A$ vyššie.)

Skalár je číselná hodnota. Môžeme ju pripočítať alebo odpočítať od ľubovoľnej súradnice bodu alebo vektora, a tiež ňou môžeme vynásobiť alebo vydeliť ľubovoľnú súradnicu bodu alebo vektora. Vo všetkých prípadoch bude výsledkom opäť bod alebo vektor.