7. Olympiáda vo vyhľadávaní v texte vzorové riešenie

text[1..n] // text dlzky n, v ktorom vyhladavame
slovo[1..m] // slovo dlzky m, ktore hladame v texte
counter = 0

// postupne skusime kazdu poziciu textu ako zaciatok slova
for i = 1 to n:
  // zlava doprava overime, ci sa tam nachadza slovo
  for j = 1 to m:
    if i + j - 1 > n:
      break
    counter += 1
    if text[i + j - 1] != slovo[j]:
      // lisi sa v j-tom znaku, slovo urcite nezacina na pozicii i v texte
      break
    if j == m:
      // nasli sme vyskyt slova v texte, podame o tom oznam a pokracujeme dalej vo vyhladavani

aaaa
aab

9

V texte budeme označovať veľkosť vstupu ako \(n\). Teda dĺžka textu aj dĺžka slova sú \(O(n)\). Zjednoduší nám to analýzu časovej zložitosti – neberieme dĺžku textu a dĺžku slova ako dve rôzne premenné.

Naivné riešenie

Samotné zadanie nám dáva návod, ako získať nejaké body za túto úlohu. Implementujeme naivný algoritmus, a počítame si počet porovnaní.

#include <iostream>
#include <string>
using namespace std;

int main () {
  string text, slovo;
  cin >> text >> slovo;
  
  long long vysledok = 0;
  for (int i = 0; i < (int) text.size(); i++) {
    for (int j = 0; j < (int) slovo.size(); j++) {
      if (i + j >= (int) text.size()) {
        break;
      }
      vysledok++;
      if (text[i + j] != slovo[j]) {
        break;
      }
    }
  }
  cout << vysledok << "\n";  
  return 0;
}

Ďalej si ukážeme tri riešenia. Prvé dve na seba nadväzujú, a síce nie sú z časového hľadiska optimálne, ale majú zaujímavú myšlienku, ktorá sa často dá uplatniť aj v iných úlohách. Kľudne ale môžete začať čítať od tretieho (optimálneho) riešenia.

Šikovnejšie porovnávanie

Predstavme si, že by sme vedeli rýchlo porovnávať nie len znak textu so znakom slova, ale aj súvislý blok textu dĺžky \(a\) so súvislým blokom slova rovnakej dĺžky. Potom by sme vedeli pre každú začiatočnú pozíciu rýchlejšie zistiť, koľko porovnaní od nej spravíme:

1. Porovnávame bloky, kým sa zhodujú. Každé blokové porovnanie zodpovedá \(a\) jednotkovým porovnaniam, teda vždy, keď sa bloky zhodujú, zvýšime výsledok o \(a\). Týchto blokových porovnaní nemôže byť viac ako \(O(\frac{n}{a})\).

2. Keď narazíme na nezhodu blokov (alebo keď do konca textu alebo slova ostáva menej ako \(a\) znakov), začneme porovnávať znak po znaku. Týchto porovnaní spravíme najviac \(a\), lebo vieme, že sa blok textu s blokom slova na niektorom znaku nezhoduje.

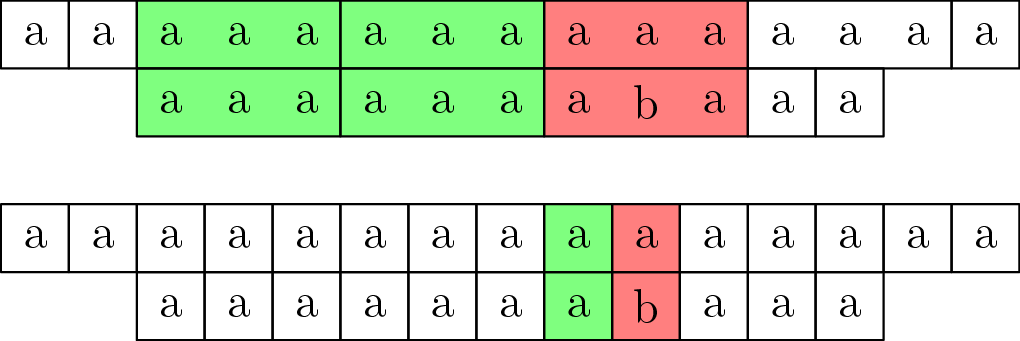
Ako ale možno bloky porovnávať rýchlejšie, ako znak po znaku? Kľúčovým pozorovaním je, že týchto blokov je iba \(O(n)\). Môžeme si preto dovoliť ich na začiatku lexikograficky usporiadať, a každému bloku priradiť počet lexikograficky menších blokov – jeho číslo. Namiesto porovnávania obsahov blokov nám teraz stačí porovnávať ich čísla, ktoré sú veľké \(O(n)\) – takže môžeme predpokladať, že sa nám zmestia do bežnej premennej a vieme ich porovnávať v konštantnom čase. To je pre dostatočne veľké bloky oveľa rýchlejšie, ako porovnávať ich znak po znaku.

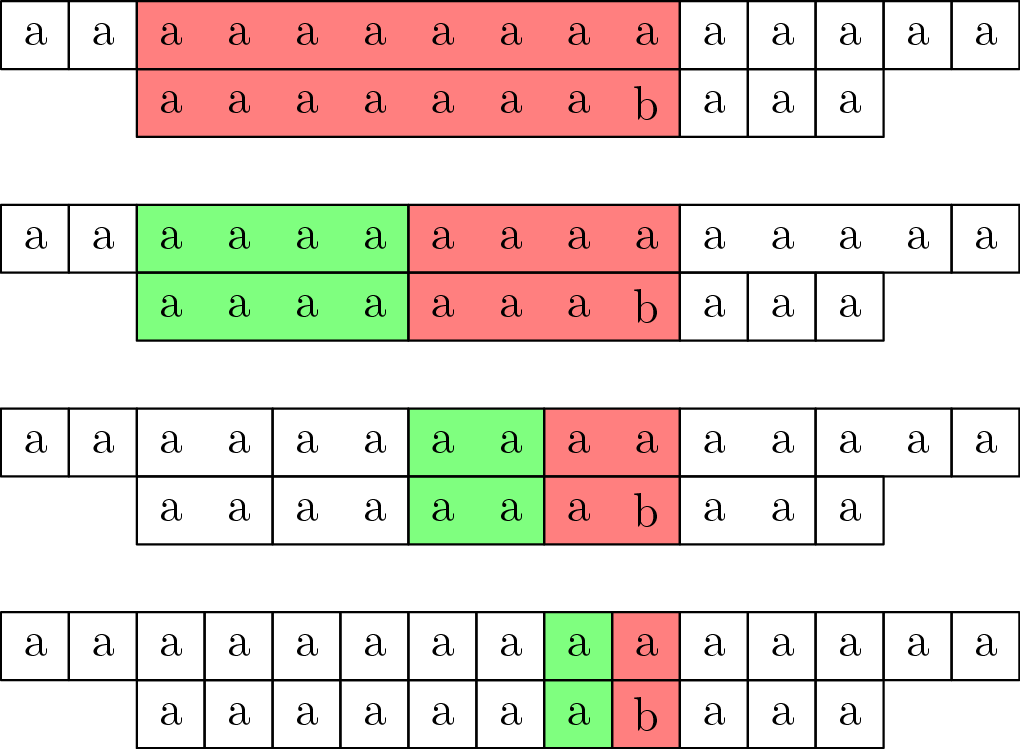
Spravíme tak \(O(\frac{n}{a} + a)\) operácii pre každú začiatočnú pozíciu – pre všetky pozície to potom trvá \(O(n \cdot (\frac{n}{a} + a))\).

Ešte musíme započítať čas strávený zisťovaním čísel blokov. Máme ich \(O(n)\), a porovnanie dvoch blokov trvá \(O(a)\) – takže triedenie nám bude trvať \(O(n \log {n} \cdot a)\).

Vhodná voľba \(a\) je \(a = \sqrt{n}\), pre ktorú dostávame celkovú časovú zložitosť \(O(n \sqrt{n} \log{n})\). Pamäťová zložitosť je \(O(n \sqrt {n})\) – najviac si toho pamätáme v zozname blokov, ktorých je \(O(n)\), a každý má dĺžku \(O(\sqrt{n})\).

#include <algorithm>
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;

struct Blok {
  string obsah;
  int kto, zaciatok;
  
  Blok (string a, int b, int c) : obsah(a), kto(b), zaciatok(c) {}
  
  bool operator< (const Blok b) const { // pouziva sa pri sorte
    return obsah < b.obsah;
  }
};

int main () {
  string retazec[2]; // retazec[0] je text, retazec[1] je slovo
  cin >> retazec[0] >> retazec[1];
  int dlzkaBloku = ceil(sqrt(min(retazec[0].size(), retazec[1].size())));
  
  // ocislujeme bloky
  vector<Blok> zoznam;
  vector<int> cisloBloku[2]; // cisloBloku[0] su cisla blokov v texte, cisloBloku[1] zas v slove
  for (int kto = 0; kto < 2; kto++) {
    int dlzka = (int) retazec[kto].size() - dlzkaBloku + 1;
    cisloBloku[kto].resize(dlzka);
    for (int i = 0; i < dlzka; i++) {
      zoznam.push_back(Blok(retazec[kto].substr(i, dlzkaBloku), kto, i));
    }
  }
  sort(zoznam.begin(), zoznam.end());
  int pocetMensich = 0;
  for (int i = 0; i < (int) zoznam.size(); i++) {
    if (i > 0) {
      if (zoznam[i - 1] < zoznam[i]) {
        pocetMensich++;
      }
    }
    cisloBloku[zoznam[i].kto][zoznam[i].zaciatok] = pocetMensich;
  }
  
  // samotne porovnavanie
  long long vysl = 0;
  for (int i = 0; i < (int) retazec[0].size(); i++) {
    int j = 0;
    while (i + j < (int) cisloBloku[0].size() && j < (int) cisloBloku[1].size()) {
      if (cisloBloku[0][i + j] == cisloBloku[1][j]) {
        j += dlzkaBloku;
        vysl += dlzkaBloku;
      }
      else {
        break;
      }
    }
    while (i + j < (int) retazec[0].size() && j < (int) retazec[1].size()) {
      vysl++;
      if (retazec[0][i + j] != retazec[1][j]) {
        break;
      }
      j++;
    }
  }
  cout << vysl << "\n";
  return 0;
}

Na štýl binárneho vyhľadávania

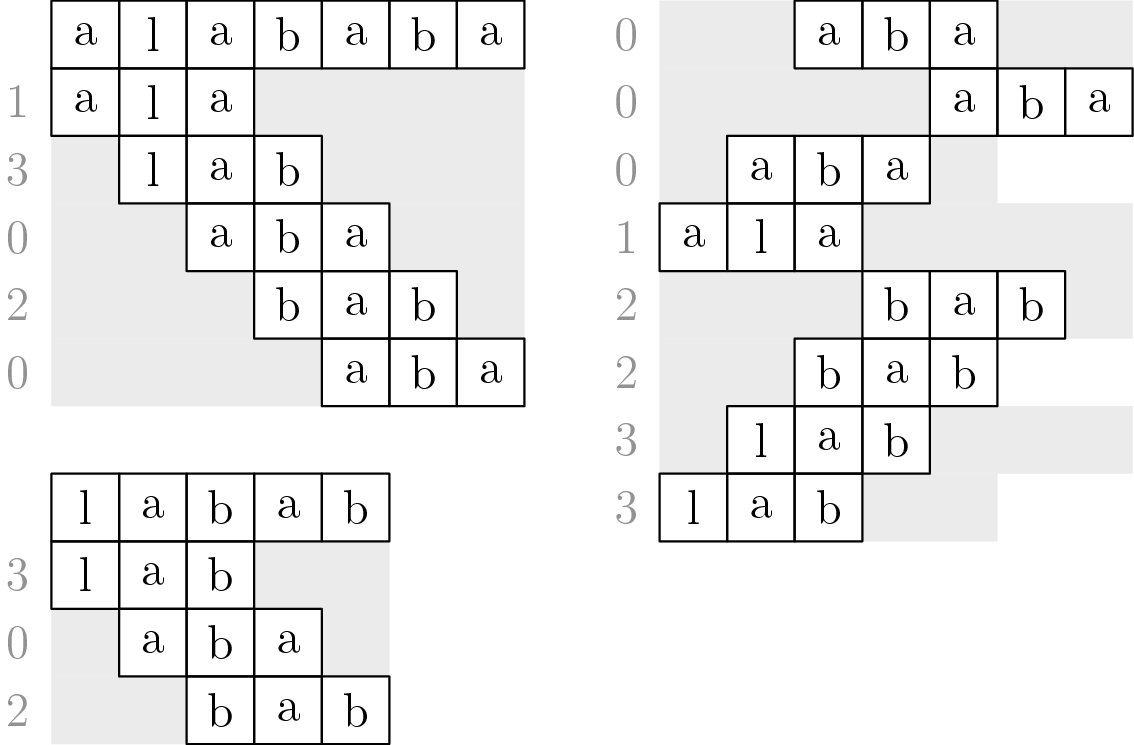
Nemusíme mať ale iba jednu veľkosť blokov. Bloky si môžeme rozdeliť do viacerých úrovní podľa ich dĺžky, a na každej úrovni ich očíslovať lexikograficky. Ďalej nám opäť stačí namiesto porovnávania obsahov blokov porovnávať ich čísla. Porovnávanie začneme na najvyššej úrovni. Vždy, keď nájdeme nezhodu, začneme porovnávať bloky o úroveň nižšie. Na najnižšej úrovni budú bloky dĺžky \(1\), teda samotné znaky.

Potrebujeme teda vhodne zvoliť dĺžky blokov na jednotlivých úrovniach, a šikovne bloky na každej úrovni očíslovať lexikograficky. Vhodnou voľbou, ktorá vyrieši oba problémy, je mať na každej úrovni bloky práve dvakrát také dlhé, ako bloky na o \(1\) nižšej úrovni.

Pri porovnávaní budeme mať na každej úrovni najviac \(1\) zhodu – \(2\) zhody by totiž zodpovedali \(1\) zhode na úrovni vyššie. Na aktuálnu úroveň sme sa ale mohli dostať iba tak, že na vyššej úrovni nastala nezhoda. Úrovní máme \(O(\log {n})\), takže by sme mali iba \(O(\log{n})\) blokových porovnaní pre každú začiatočnú pozíciu. Každé blokové porovnanie trvá \(O(1)\) (porovnávame čísla veľké \(O(n)\)), táto časť algoritmu teda trvá \(O(n \log {n})\).

A ako nájdeme lexikografické číslovanie pre každú úroveň? Tentokrát si nemôžeme dovoliť bloky usporiadať podľa ich obsahu – môžu byť totiž dlhé až \(O(n)\), a normálne triedenie by trvalo až \(O(n^2 \log {n})\). Kľúčovým pozorovaním je, že blok na každej úrovni (okrem najnižšej úrovne) zodpovedá dvom blokom na úrovni o \(1\) nižšej. Ak tie už máme očíslované, vieme ľahko porovnávať ľubovoľné dva bloky na aktuálnej úrovni – najprv ich porovnáme podľa prvej polovice, a ak sa na nej zhodujú, tak ich porovnáme podľa druhej polovice. Keď vieme bloky porovnávať, tak ich vieme usporiadať a následne očíslovať.

Úrovní je \(O(\log {n})\), na každej triedime \(O(n)\) blokov, a každé porovnanie trvá \(O(1)\) (lebo dvakrát porovnávame čísla veľké \(O(n)\)). Preto má táto časť algoritmu časovú zložitosť \(O(n \log^2 {n})\).

Celková časová zložitosť je teda \(O(n \log^2 {n})\). Pamäťová zložitosť je \(O(n \log {n})\) – najviac pamäte zaberajú úrovne, ktorých je \(O(\log{n})\), a na každej si pamätáme čísla blokov, ktorých je \(O(n)\).

#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;

struct Blok {
  int prvaPolka, druhaPolka;
  int kto, zaciatok;
  
  Blok (int a, int b, int c, int d) : prvaPolka(a), druhaPolka(b), kto(c), zaciatok(d) {}
  
  bool operator< (const Blok b) const { // pouziva sa pri sorte
    if (prvaPolka == b.prvaPolka) {
      return druhaPolka < b.druhaPolka;
    }
    return prvaPolka < b.prvaPolka;
  }
};

int main () {
  string retazec[2]; // retazec[0] je text, retazec[1] je slovo
  cin >> retazec[0] >> retazec[1];
  
  vector<vector<int> > cisloBloku[2]; // cisloBloku[0] su cisla blokov v texte, cisloBloku[1] zas v slove
  
  // ocislujeme jednotkove bloky
  for (int kto = 0; kto < 2; kto++) {
    int dlzka = retazec[kto].size();
    cisloBloku[kto].resize(dlzka);
    for (int i = 0; i < dlzka; i++) {
      int cislo = 'a' - retazec[kto][i] - 1; // jednotkove bloky maju cisla -1 az -26
      cisloBloku[kto][i].push_back(cislo);
    }
  }
  // ocislujeme postupne bloky velkosti 2, 4, 8, ...
  int level = 0;
  int krok = 2;
  while (krok <= min(retazec[0].size(), retazec[1].size())) {
    vector<Blok> zoznam;
    for (int kto = 0; kto < 2; kto++) {
      for (int i = 0; i + krok <= (int) retazec[kto].size(); i++) {
        int prvaPolka = cisloBloku[kto][i][level];
        int druhaPolka = cisloBloku[kto][i + krok / 2][level];
        zoznam.push_back(Blok(prvaPolka, druhaPolka, kto, i));
      }
    }
    sort(zoznam.begin(), zoznam.end());
    int pocetMensich = 0;
    for (int i = 0; i < (int) zoznam.size(); i++) {
      if (i > 0) {
        if (zoznam[i - 1] < zoznam[i]) {
          pocetMensich++;
        }
      }
      cisloBloku[zoznam[i].kto][zoznam[i].zaciatok].push_back(pocetMensich);
    }
    level++;
    krok *= 2;
  }
  
  // samotne porovnavanie
  long long vysl = 0;
  for (int i = 0; i < (int) retazec[0].size(); i++) {
    int j = 0;
    int level = (int) cisloBloku[1][0].size() - 1;
    int krok = (1 << level);
    while (level != -1) {
      if (i + j >= (int) retazec[0].size()) {
        break;
      }
      if (j >= (int) retazec[1].size()) {
        break;
      }
      if (level < (int) cisloBloku[0][i + j].size()) {
        if (level < (int) cisloBloku[1][j].size()) {
          if (cisloBloku[0][i + j][level] == cisloBloku[1][j][level]) {
            j += krok;
            vysl += krok;
          }
        }
      }
      level--;
      krok /= 2;
    }
    if (j < (int) retazec[1].size() && i + j < (int) retazec[0].size()) {
      vysl++;
    }
  }
  cout << vysl << "\n";
  return 0;
}

Toto riešenie sa dá vylepšiť tak, aby malo optimálnu časovú zložitosť \(O(n)\) za využitia kladív ako sufixové pole, LCP pole, a range-minimum query. Tie výrazne presahujú rámec tejto úlohy, a uvádzať ich tu nebudeme.

Čo navrhujú Knuth, Morris a Pratt

Predstavme si, že sa nám znaky textu odkrývajú postupne. Na začiatku máme teda prázdny text, a postupne na jeho koniec pridávame znaky. Ako sa bude meniť počet porovnaní, ktoré spraví naivný algoritmus?

Pozrime sa na nejakú začiatočnú pozíciu. Od nej spravíme niekoľko porovnaní, až kým nenastane jedno z nasledujúcich:

1. Našli sme nezhodu. Potom keď na koniec textu pridáme nový znak, tak počet porovnaní, ktoré spravíme pre túto začiatočnú pozíciu, sa nezmení.

2. Nenašli sme nezhodu, a došli sme na koniec slova. Pridaním znaku na koniec textu sa počet porovnaní, ktoré spravíme, opäť nezmení – nie je s čím ďalej porovnávať, lebo sme na konci slova.

3. Nenašli sme ešte nezhodu, došli sme na koniec textu ale nie sme ešte na konci slova. Keď na koniec textu pridáme nový znak, tak určite spravíme jedno ďalšie porovnanie.

Zaujíma nás teda počet tých začiatkov, pri ktorých sme došli na koniec textu ale ešte nie sme na konci slova. Každému takému začiatku zodpovedá reťazec znakov, ktorý sme už spracovali, a ktorý sa zhodoval s prvými niekoľkými znakmi slova. Je to teda vlastný prefix slova. Takže keď pridávame znak na koniec textu, výsledok sa zvýši o počet vlastných prefixov slova, ktoré sú sufixom textu (pred pridaním nového znaku).

Toto nám umožňuje spočítať práve Knuthov-Morrisov-Prattov algoritmus. Konkrétne

1. Vieme s jeho pomocou po pridaní každého znaku zistiť najdlhší prefix slova, ktorý je sufixom textu.

2. Najdlhší prefix slova, ktorý je sufixom textu, nám jednoznačne určuje všetky prefixy slova, ktoré sú sufixami textu. To vyplýva z toho, že tie sú kratšie – takže ak sú sufixami textu, musia byť aj sufixami nášho najdlhšieho prefixu.

3. Pre každý prefix slova vieme jeho najdlhší vlastný sufix taký, že je zároveň prefixom slova – takzvané spätné linky.

4. Ak postupne budeme uvažovať prefix, na ktorý ukazuje naša spätná linka, potom prefix, na ktorý ukazuje spätná linka predchádzajúceho prefixu, … tak vytvoríme postupnosť všetkých prefixov slova takých, že sú sufixom nášho najdlhšieho prefixu.

5. Nás zaujíma ich počet. Ak ho pre i-ty prefix slova označíme pocet[i], a spätnú linku z i-teho prefixu ako spat[i], tak pocet[i] = pocet[spat[i]] + 1. Takto vypočítame všetky počty.

6. Ak je najdlhším prefixom celé slovo, tak odrátame od výsledku \(1\), nakoľko sme ho zarátali v predchádzajúcom procese, a nemali sme ho zarátať.

Časová aj pamäťová zložitosť sú \(O(n)\).

#include <iostream>
#include <string>
#include <vector>
using namespace std;

int precitaj (char znak, string& slovo, vector<int>& spatneLinky, int stav) {
  if (stav + 1 < (int) spatneLinky.size()) {
    if (znak == slovo[stav]) {
      return stav + 1;
    }
  }
  while (stav != 0) {
    stav = spatneLinky[stav];
    if (znak == slovo[stav]) {
      return stav + 1;
    }
  }
  return 0;
}

int main () {
  string text, slovo;
  cin >> text >> slovo;
  
  vector<int> spatneLinky(1, 0);
  vector<int> dlzkaChvostu(1, 0);
  for (int i = 0; i < (int) slovo.size(); i++) {
    int predch = precitaj(slovo[i], slovo, spatneLinky, i);
    spatneLinky.push_back(predch);
    dlzkaChvostu.push_back(1 + dlzkaChvostu[predch]);
  }
  
  long long vysl = 0;
  int stav = 0;
  for (int i = 0; i < (int) text.size(); i++) {
    if (stav != (int) slovo.size()) {
      vysl++;
    }
    vysl += dlzkaChvostu[stav];
    stav = precitaj(text[i], slovo, spatneLinky, stav);
  }
  cout << vysl << "\n";
  return 0;
}