Knuth-Morris-Prattov algoritmus

Problém vyhľadávania v texte

Problém vyhľadávania v texte je daný nasledovne: máme reťazec dĺžky $n$ zvaný text a reťazec dĺžky $m \leq n$ zvaný vzor. Naším cieľom je nájsť všetky výskyty vzoru v texte.

Napríklad, ak text je gamagmagmamamagamagma a vzor je magma, vyskytuje sa vzor v texte trikrát (prvý výskyt začína na treťom písmene textu, druhý na šiestom a tretí na sedemnástom).

Knuth-Morris-Prattov algoritmus tento problém rieši v čase $O(n + m)$. V tomto článku sa k nemu postupne dopracujeme. Začneme od naivného algoritmu.

Naivný algoritmus

Jednoduché ale pomalé riešenie problému vyhľadávania spočíva v tom, že vyskúšame všetky možné pozície vzoru v texte. Pre každú pozíciu znak po znaku skontrolujeme, či sa tam nachádza vzor.

/* Funkcia vráti zoznam pozícií v texte, na ktorých začínajú
 * jednotlivé výskyty vzoru.
 */
vector<int> najdi_vyskyty(string text, string vzor)
{
    vector<int> vysledok;

    /* Vyskúšame všetky možné pozície */
    for(int zaciatok = 0; zaciatok + vzor.size() <= text.size(); zaciatok++)
    {
        /* V tejto premennej si pamätáme, či doteraz všetky znaky sedeli */
        bool sedi = true;

        /* Vyskúšame, či sedia všetky znaky */
        for(int i=0; i<vzor.size(); i++)
        {
            /* Ak i-ty znak nesedí, nemá zmysel skúšať ďalej */
            if(vzor[i] != text[zaciatok + i])
            {
                sedi = false;
                break;
            }
        }

        /* Ak všetky znaky sedeli, našli sme výskyt */
        if(sedi)
        {
            vysledok.push_back(zaciatok);
        }
    }
    return vysledok;
}

Keďže skúšame $n - m + 1$ začiatočných pozícií a pre každú pozíciu musíme v najhoršom prípade porovnať všetky písmená vzoru, ktorých je $m$, výsledná časová zložitosť je $O((n-m) \cdot m)$, čo pre $n >> m$ je $O(n \cdot m)$.

Zlepšenie

Všimnime si podrobnejšie horeuvedený algoritmus. Pri skúmaní, či na $i$-tom mieste v texte začína vzor, sa môže stať, že prvých $j$ písmeniek vzoru sa zhoduje s textom, ale $j+1$-vé písmenko sa už nezhoduje. Teraz by sme sa vrátili a skúšali, či vzor nezačína na $i+1$-vom písmenku. Predstavme si však, že vzor je napríklad baaaaaaaa a zistíme, že prvých $j$ písmenok sa zhoduje s textom a $j+1$-vé už nie. V tomto špeciálnom prípade sa teraz nemusíme vracať až na $i+1$-vú pozíciu, pretože vieme, že najbližších $j-1$ písmen po $i$-tom sú a-čka, teda tam nemôže začínať vzor. Preto môžeme ďalej pokračovať až na $i+j$-tom písmenku textu.

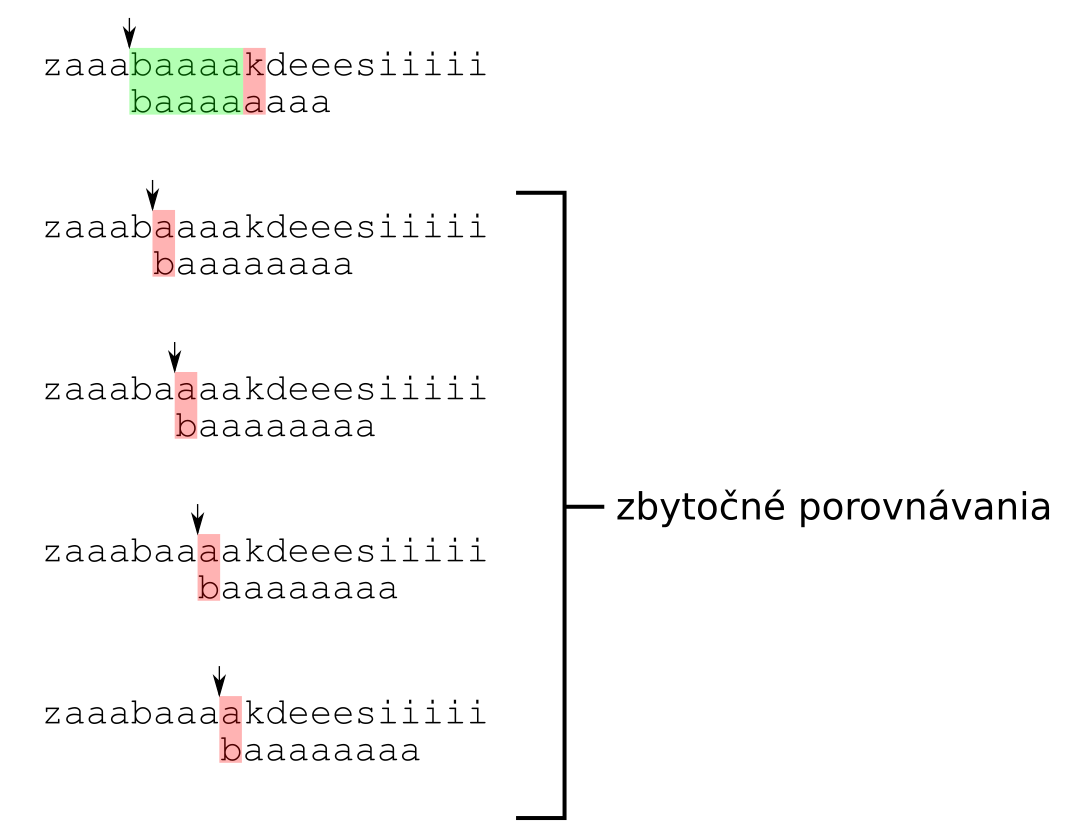
Nemôžeme ale vždy preskočiť hneď všetkých $j-1$ písmeniek. Napríklad si predstavme, že v texte bababaabbbaba hľadáme vzor babaabbb. Keď budeme skúšať, či na prvom mieste v texte začína vzor, tak na piatom mieste zistíme, že písmenká sa nezhodujú. Ak by sme teraz preskočili ďalšie 3 písmená a začali hľadať až od piatej pozície, nenašli by sme výskyt začínajúci na tretej pozícii.

Zovšeobecnenie

Ako teda túto myšlienku zovšeobecniť pre ľubovoľný vzor? Uvedomme si, že v okamihu, keď sme pri $j+1$-vom písmene vzoru zistili, že sa nezhoduje s textom, vieme, že prechádzajúcich $j$ znakov textu tvorí prefix (začiatočný podreťazec) vzoru. Teraz potrebujeme vedieť, o koľko najmenej znakov musíme vzor "posunúť doprava", aby nám pasoval na koniec doteraz prečítaného textu.

Nuž, ale ako sme si povedali, koniec prečítaného textu je vlastne začiatkom vzoru. Takže vlastne potrebujeme pre každý prefix vzoru vedieť, o koľko posunutý vzor naň opäť pasuje. (V príklade hore: keď sme hľadali vzor na 5. pozícii, zistili sme, že prvé 4 znaky pasujú, piaty nie. Teraz sme teda v situácií, že na aktuálnom konci textu je prefix vzoru dĺžky 4. Vidíme, že keď zoberieme len prvé dva znaky vzoru, budú opäť pasovať na aktuálny koniec textu.)

Pre každú dĺžku prefixu $j$ vo vzore si teda vypočítame číslo $\mathrm{next}(j)$ s nasledovným významom:

• Ak posledných $j$ prečítaných písmen textu tvorí prefix vzoru, potom aj posledných $\mathrm{next}(j)$ prečítaných písmen tvorí prefix vzoru. Číslo $\mathrm{next}(j)$ je pritom najväčšie číslo menšie než $j$ s touto vlastnosťou.

Inými slovami, $\mathrm{next}(j)$ je najväčšie číslo menšie než $j$ také, že prefix vzoru dĺžky $\mathrm{next}(j)$ je sufixom prefixu vzoru dĺžky $j$.

Napríklad pre vzor kukučka nadobúda funkcia $\mathrm{next}(j)$ postupne hodnoty $0, 0, 1, 2, 0, 1, 0$:

Všimnime si, že funkcia $\mathrm{next}()$ je závislá iba od vzoru. Jej hodnoty si teda môžeme predpočítať pred samotným vyhľadávaním v texte.

Vyhľadávanie

Na chvíľu sa tvárme, že už máme funkciu $\mathrm{next}()$ predpočítanú a pozrime sa, ako s jej pomocou budeme vyhľadávať v texte.

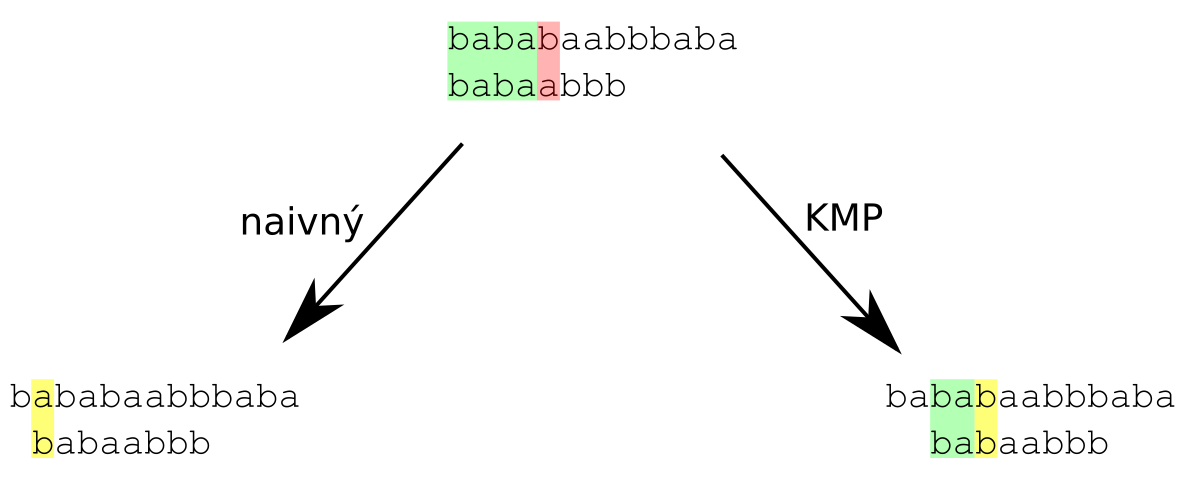
Náš algoritmus bude vyzerať podobne ako naivný algoritmus uvedený za začiatku tohto článku. Líšiť sa budú iba v momente, keď nájdu nezhodu medzi písmenom v texte a vzorom.

Povedzme, že sme overovali, či je v texte výskyt vzoru začínajúci na $i$-tom písmene textu, prvých $j$ písmen vzoru sedelo s textom, ale $j+1$-vé písmeno vzoru už nesedí s $i+j$-tym písmenom textu. Naivný algoritmus by v tomto momente posunul začiatok hľadaného výskytu na $i+1$-vú pozíciu v texte a začal by zhodu vzoru s textom kontrolovať od začiatku.

My však vieme, že najbližší ďalší možný začiatok vzoru je na pozícii $i + (j - \mathrm{next}(j))$ a preto skočíme rovno na tento začiatok. Tiež vieme, že pri tomto začiatku prvých $\mathrm{next}(j)$ písmen zaručene sedí s textom. Preto ich ani nebudeme kontrolovať. Overovanie zhody teda začneme od $\mathrm{next}(j)+1$-vého znaku vzoru, ktorý porovnáme s $i+j$-tym znakom textu.

Podobná situácia nastane, keď náš algoritmus nájde výskyt vzoru v texte. Vtedy si tento výskyt (rovnako ako naivný algoritmus) poznačíme a posunieme začiatok overovanej časti textu. Narozdiel od naivného algoritmu však tento začiatok neposunieme iba o jednu pozíciu, ale o $m - \mathrm{next}(m)$ pozícií ($m$ je dĺžka vzoru) a pri overovaní preskočíme prvých $\mathrm{next}(m)$ znakov vzoru (keďže tie zaručene pasujú).

Analýza zložitosti

Tento algoritmus má zložitosť $O(n)$. Prečo? Predstavme si, že máme červenú a modrú mincu, ktoré budú v každom okamihu položené pri nejako písmene textu:

• Červená minca bude vždy na začiatku potenciálneho výskytu vzoru, ktorý práve overujeme
• Modrá minca bude vždy na tom písmene textu, ktoré budeme najbližšie porovnávať s písmenom vo vzore.

Na začiatku sú teda obe mince na prvom písmene textu.
Vždy, keď porovnáme nejaký znak vzoru so znakom textu, stane sa jedna z dvoch vecí:

• Znaky sú rovnaké. V takom prípade sa posúvame v čítaní textu ďalej, pričom začiatok overovanej časti textu ostáva na miese. Modrá minca sa teda posunie o jednu pozíciu doprava a červená ostáva na mieste (vynímkou je, keď nájdeme výskyt vzoru -- v takom prípade sa pohne aj červená minca doprava).

• Znaky sú rôzne. V takom prípade sa posunie začiatok overovanej časti textu dopredu, teda červená minca sa posunie o niekoľko pozícií doprava. V najbližšom porovnávaní budeme porovnávať ten istý znak textu (s iným znakom vzoru), takže modrá minca sa nepohne.

Žiadna minca sa nikdy nehýbe doľava. To znamená, že žiadna minca sa nemôže hýbať viac než $n$-krát (lebo by sa dostala za koniec textu), teda dokopy sa mince môžu hýbať maximálne $2n$ krát. Pri každom porovnaní sa pritom niektorá minca hýbe. To znamená, že dokopy urobíme najviac $2n$ porovnaní. Okrem porovnávania znakov robíme ešte nejakú réžiu, tej je však rádovo rovnako veľa ako porovnaní (nikdy sa v našom algoritme nestane, že by sme robili veľa operácií po sebe bez toho, aby sme porovnávali nejaké znaky textu a vzoru). Preto má vyhľadávanie zložitosť $O(n)$.

Predpočítanie funkcie next()

Ostáva ešte vyriešiť predpočítanie funkcie $\mathrm{next}()$. To sa dá robiť naivne v čase $O(m^3)$, prípadne trochu prefíkanejšie v čase $O(m^2)$, my si však ukážeme, ako to robiť ešte rýchlejšie.

Budeme postupne počítať hodnoty $\mathrm{next}(1), \mathrm{next}(2), \dots, \mathrm{next}(m)$, v takomto poradí. Pri výpočte hodnoty $\mathrm{next}(j)$ teda už budeme poznať hodnoty $\mathrm{next}(1), \mathrm{next}(2), \dots, \mathrm{next}(j-1)$.

Keď počítame hodnotu $\mathrm{next}(j)$, mohli by sme si zobrať prefix vzoru dĺžky $j$ a potom postupne skúšať, či naňho pasujú¹ prefixy dĺžok $j-1, j-2, \dots$, až kým by sme nenašli prvý, ktorý pasuje (vždy nájdeme nejaký pasujúci prefix, lebo prefix dĺžky 0 pasuje na všetko). Dĺžka tohto prefixu je potom hľadané $\mathrm{next}(j)$. Uvedomme si však nasledovnú vec: ak prefix dĺžky $k$ (kde $k < j$) pasuje na prefix dĺžky $j$, potom prefix dĺžky $k-1$ určite pasuje na prefix dĺžky $j-1$ (okrem špeciálneho prípadu, keď $k=0$). Obrátene: na to, aby prefix dĺžky $k>0$ mal aspoň teoretickú šancu pasovať na prefix dĺžky $j$, musí prefix dĺžky $k-1$ pasovať na prefix dĺžky $j-1$. To znamená, že najdlhší prefix, ktorý má zmysel skúšať, je prefix dĺžky $\mathrm{next}(j-1)+1$. (číslo $\mathrm{next}(j-1)+1$ si označme $k_1$).

Pri skúšaní tohto prefixu pritom stačí overiť, či pasuje posledný znak, teda či $k_1$-ty znak vzoru je rovnaký ako $j$-ty. Z toho, ako sme určili číslo $k_1$, totiž vyplýva, že prefix dĺžky $k_1-1$ pasuje na prefix dĺžky $j-1$, teda všetky znaky prefixu dĺžky $k_1$ (okrem posledného) sa určite budú zhodovať so zodpovedajúcimi znakmi prefixu dĺžky $j$.

Čo ak sa $k_1$-ty znak nezhoduje s $j$-tym? Vyskúšame najbližší kratší prefix, ktorý má šancu pasovať. Vieme, že aby prefix dĺžky $k>0$ mal šancu pasovať na prefix dĺžky $j$, musí prefix dĺžky $k-1$ pasovať na prefix dĺžky $j-1$. Keďže už vieme, že $k < k_1$ a prefix dĺžky $k_1-1$ pasuje na prefix dĺžky $j-1$, prefix dĺžky $k-1$ bude pasovať aj na prefix dĺžky $k_1$. To znamená, že ďalší prefix, ktorý má zmysel skúšať, je prefix dlhý $\mathrm{next}(k_1-1)+1$ (toto číslo si označme $k_2$). Aj pri skúšaní tohto prefixu nám stačí overiť iba posledné písmeno. Ak ani prefix dĺžky $k_2$ nepasuje na prefix dĺžky $j$, vyskúšame prefix dĺžky $k_3 = \mathrm{next}(k_2-1)+1$ a takto pokračujeme až kým nenájdeme pasujúci prefix, prípadne nezistíme, že žiaden prefix dĺžky aspoň $1$ nepasuje na prefix dĺžky $j$ a v takom prípade $\mathrm{next}(j) = 0$.

Keď sa na tento algoritmus lepšie pozrieme, môžeme si všimnúť, že predpočítavanie funkcie $\mathrm{next}()$ sa dosť podobá na samotné vyhľadávanie v texte. Keď sa naňho pozrieme ešte lepšie, všimneme si, že pri predpočítavaní $\mathrm{next}()$ budeme robiť presne tie isté porovnania ako by sme robili, keby sme náš vzor vyhľadávali v texte vyzerajúcom ako vzor bez prvého písmena. Z podobných dôvodov ako vyhľadávanie, aj predpočítavanie funkcie $\mathrm{next}()$ teda bude trvať lineárny čas, v tomto prípade $O(m)$.

Celková zložitosť algoritmu KMP je teda $O(n+m)$.

Implementácia

Nakoniec si ešte ukážeme dve implementácie nášho algoritmu (obe v C++). Prvá z nich sa viac drží označení použitých v tomto texte. Druhá si niektoré veci pamätá trochu inak, ale je elegantnejšia.

Prvá implementácia:

vector<int> KMP(string text, string vzor)
{
    int n = text.size(), m = vzor.size();

    //hodnoty funkcie next. Hodnotu next[0] nepoužijeme.
    vector<int> next(m+1); 


    //Predrátanie funkcie next
    next[1] = 0;
    for(int j=2; j<=m; j++)
    {
        int k = next[j-1]+1;

        //Znižujeme premennú k až kým nenájdeme pasujúci prefix.
        //Mínus jednotky sú v indexoch, lebo číslujeme od nuly.
        while(vzor[k-1] != vzor[j-1]) 
        {
            if(k == 1)
            {
                k = 0;
                break;
            }
            k = next[k-1]+1;
        }
        next[j] = k;
    }

    //Hľadanie výskytu

    vector<int> vysledok; //sem si budeme ukladat pozicie vyskytov

    int zaciatok = 0; //začiatok overovanej časti textu (červená minca)
    int aktualny = 0; //znak textu, na ktorý sa ideme pozerať (modrá minca)
    while(aktualny < n && zaciatok < n)
    {
        int j = aktualny - zaciatok; //počet znakov vzoru, ktoré nám zatiaľ sedia
        if(text[aktualny] == vzor[j]) //znaky pasujú
        {
            aktualny++;
            if(aktualny - zaciatok == m) //nasli sme vyskyt
            {
                vysledok.push_back(zaciatok);
                zaciatok += m-next[m];
            }
        }
        else //znaky nepasujú
        {
            if(zaciatok == aktualny) //nefunguje ziaden zaciatok pred aktualnym znakom
            {
                zaciatok++;
                aktualny++;
            }
            else
            {
                zaciatok += j - next[j];
            }
        }
    }
    return vysledok;
}

Druhá implementácia

V tejto implemenácii si dodefinujeme $\mathrm{next}(0)$ ako $-1$, čo nám vyrieši zopár špeciálnych prípadov. Pri samotnom prechádzaní textu si potom nepamätáme začiatok výskytu ktorý kontrolujeme, ale písmeno textu na ktorom sme (premenná i) a počet znakov vzoru, ktoré zatiaľ sedia (premenná position, v predošlej implementácii v tejto úlohe vystupovalo j).

vector<int> KMP(string text, string pattern)
{
    vector<int> next(pattern.size()+1);

    //Compute next
    next[0] = -1;
    for(int i=0; i<pattern.size(); i++)
    {
        int back = next[i];
        while(back >= 0 && pattern[i] != pattern[back]) back = next[back];
        next[i+1] = back+1;
    }

    //Process the string
    vector<int> result;
    int position = 0;
    for(int i=0; i<text.size(); i++)
    {
        while(position >= 0 && text[i] != pattern[position]) position = next[position];
        position++;
        if(position == pattern.size())
        {
            result.push_back(i+1-pattern.size());
            position = next[position];
        }
    }
    return result;
}