Zadanie
Baklažánovi sa nechcelo vymýšľať rozprávku do tejto úlohy a tak si aspoň na papieri vyznačil niekoľko bodov. Po chvíli za ním prišiel Buj, a aby reč nestála sa ho začal pýtať otázky typu: “Koľko tvojich bodov leží v trojuholníku danom týmito tromi bodmi?”. Baklažánovi odpovedanie na tieto otázky dalo vcelku zabrať a teraz ponúka odmenu 20 bodov každému, kto to zvládne tiež.
Úloha
V rovine máme vyznačených \(n\) rôznych bodov s celočíselnými súradnicami. Dostanete \(q\) otázok typu “Koľko vyznačených bodov leží v trojuholníku \(ABC\)?”, kde \(A, B, C\) sú tri rôzne vyznačené body. Vašou úlohou je všetky tieto otázky správne zodpovedať. Strany a vrcholy trojuholníka považujeme za jeho súčasť.
Formát vstupu
V prvom riadku vstupu je jedno celé číslo \(n\) (\(3 \leq n \leq 500\)) – počet bodov. Nasleduje \(n\) riadkov popisujúcich jednotlivé body. V každom z týchto riadkov budú dve celé čísla \(x\) a \(y\) (\(|x|, |y| \leq 1\,000\,000\,000\)) – súradnice daného bodu. Všetky body budú navzájom rôzne. Body si očíslujme v poradí, v akom sú uvedené na vstupe číslami \(0, 1, \dots, n\). V nasledujúcom riadku je jedno celé číslo \(q\) (\(1 \leq q \leq 200\,000\)) – počet otázok. V posledných \(q\) riadkoch sú popisy týchto otázok. Každý z týchto riadkov obsahuje tri celé čísla \(a, b, c\) z rozsahu \(0\) až \(n-1\) – čísla bodov tvoriacich vrcholy trojuholníka, na ktorý sa pýtame. Je zaručené, že body \(a, b\) a \(c\) tvoria (nedegenerovaný) trojuholník.
Formát výstupu
Pre každú otázku vypíšte riadok obsahujúci jedno celé číslo – počet bodov, ktoré ležia v tomto trojuholníku alebo na jeho hranici.
Príklady
Input:
4
0 0
0 3
1 1
3 0
2
0 1 2
3 0 1Output:
3
4Naše riešenie založíme na princípe inklúzie a exklúzie (alebo ak chcete, zapojenia a vypojenia). Namiesto toho, aby sme rátali body v zadanom trojuholníku, zrátame vždy body ležiace mimo trojuholníku a ich počet odrátame od celkového počtu bodov \(n\).
Časť roviny ležiacu mimo trojuholníka \(ABC\) vieme rozdeliť na tri uhly nasledovným spôsobom:
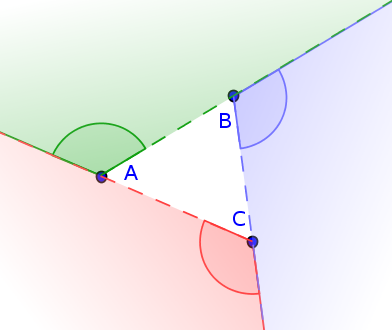
Ak si navyše povieme, že každý uhol obsahuje body ležiace na jeho ,,ľavom’‘ramene, ale neobsahuje body ležiace na jeho ,,pravom’’ ramene, ani bod ležiaci v jeho vrchole 1, bude mať naša trojica uhlov jednu dobrú vlastnosť: Každý bod roviny ležiaci mimo trohuholníka \(ABC\) leží v práve jednom z našich troch uhlov.
To znamená, že ak chceme spočítať body v našom trojuholníku, stačí nám spočítať počty bodov ležiacich v našich troch uhloch a tieto tri čísla odrátať od čísla \(n\). Body ležiace v uhle budeme počítať nasledovne:
- Každý bod \(P\), ktorý sme dostali na vstupe, spojíme myslenými polpriamkami s každým iným bodom na vstupe. Tieto polpriamky následne utriedime podľa uhla. Toto nám stačí urobiť pre každý bod raz na začiatku. Celkovo nám to teda zaberie čas \(O(n^2 \log n)\).
- Vždy, keď nás bude zaujímať počet bodov v nejakom uhle s vrcholom v \(P\), binárne vyhľadáme, kde by v našom utriedenom zozname polpriamok boli ramená tohto uhla. Počet polpriamok ležiacich medzi ramenami je počet bodov ležiacich v uhle. Počet bodov ležiacich v uhle teda vieme zistiť v čase \(O(\log n)\).
Celé riešenie teda vyzerá nasledovne:
- Po načítaní vstupu si pre každý bod predrátame zoznam polpriamok vychádzajúcich z daného bodu, utriedený podľa uhla.
- Následne spracúvame jednotlivé otázky, nasledovným spôsobom:
- Časť roviny ležiacu mimo zadaného trojuholníka si rozdelíme na tri uhly.
- Pre každý uhol vypočítame počet bodov v ňom (to nám bude trvať čas \(O(\log n)\).
- Tieto tri čísla odrátame od celkového počtu bodov \(n\) a výsledok vypíšeme.
Časová zložitosť nášho algoritmu je teda \(O((n^2 + q)\log n)\). Pamäťová zložitosť je \(O(n^2)\).
Implementačné zákernosti
Pri implementácii si bolo treba dať dobrý pozor na nasledujúce detaily:
- Správnu implementáciu triedenia a binárneho vyhľadávania podľa uhla (keďže na zoznam polpriamok sa treba pri vyhľadávaní pozerať ako na cyklický zoznam).
- Presnosť výpočtov. Ideálne bolo robiť všetko v celočíselnej aritmetike s využitím vektorových súčinov. V niektorých vstupoch boli trojice bodov, ktoré ležali takmer na priamke. Implementácia spoliehajúca sa na goniometrické funkcie a aritmetiku reálnych čísel s nimi mohla mať problém.
takéto chápanie uhlov je analogické s používaním polootvorených intervalov↩
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.