Zbierky

Korešpondenčný seminár z programovania je súťaž v programovaní a tvorbe algoritmov pre žiakov stredných škôl. Zbierky obsahujú zadania a myšlienky riešení úloh, ktoré boli v tomto seminári použité. Táto webstránka je venovaná dvom vydaniam zbierky:

• Prvá zbierka:
  • Zbierka riešených úloh Korešpondenčného seminára z programovania (1983–1998)
  • ISBN 80-88720-09-5
  • rok vydania 2006
• Druhá zbierka:
  • Zbierka riešených úloh Korešpondenčného seminára z programovania (1998–2006)
  • ISBN 978-80-88720-16-4
  • rok vydania 2011

Ako zbierky získať

Elektronické verzie je možné získať z nasledujúcich linkov:

Prvá, 'modrá' zbierka

Druhá, 'zelená' zbierka

Dopyt po fyzickej papierovej verzii je ale taký veľký, že v bežných obchodných sieťach žiadny exemplár nezoženiete :-)

Najistejší spôsob, ako sa k takýmto vzácnym zbierkam dostať, je zastaviť sa na matfyze v KSPáckej miestnosti T2. Taktiež sa k nej dá dostať na sústredku KSP, prípadne môžete ukecať nejakého KSPáka, nech vám ju donesie alebo trebárs pošle na opačný koniec sveta.

Ceny oboch zbierok sú rovné ich výrobným nákladom: prvá zbierka stojí 5 eur, druhá 6 eur.

Chyby v zbierkach

Spravili sme maximum pre to, aby ste dostali do rúk úplne dokonalé knihy. Ale život už veľakrát ukázal, že nič nemôže byť dokonalé, a tak sa nejaké chyby určite nájdu aj v našich zbierkach. Ak na nejakú narazíte, dajte nám vedieť. Prvé odhalenie ľubovoľnej logickej alebo historickej chyby v tejto zbierke ocenia autori pozvaním šťastného nálezcu na kofolu či pivo (na pivo len plnoletých!), prípadne vlastnoručným napísaním venovania do knižky. Chyby nám oznamujte na emailové adresy:

kuko [zavináč] ksp [bodka] sk, misof [zavináč] ksp [bodka] sk, ksp [zavináč] ksp [bodka] sk

Ešte predtým, ako nám však napíšete, prezrite si, prosím, nasledujúci zoznam už nájdených chýb. Ponúkaná odmena stále platí. Chyby z tohto zoznamu sa nachádzajú iba vo fyzických verziách zbierok.

Zoznam nájdených chýb v prvej zbierke

1. Zmazať vetu o škriatkovi.
2. V riešení úlohy 522 posledná veta "(Mimochodom..." nie je pravdivá.
3. V úlohách 1131 a 1521 správne meno algoritmu je "Ahov-Corasickovej algoritmus".

Zoznam nájdených chýb v druhej zbierke

1. ZMAZAŤ vetu o škriatkovi!
2. Niekoľko obrázkov nám zle vytlačili. Sú to obrázky na str. 61, str. 74 a str. 76.
3. V riešení úlohy 1643 (začiatok druhého odstavca) namiesto "Hľadáme vlastne najmenšiu hrúbku $h$ takú, že..." samozrejme hľadáme najväčšiu takú hrúbku.

Zoznam dodatkov k prvej zbierke

1. K úlohám o dláždení dominami (433 a 1344) existuje aj lepšie riešenie ako to uvedené v zbierke, pozrite napr. http://portal.acm.org/citation.cfm?id=942530.942535

2. Malý lenivý krtko z úlohy 943 má aj ľahšie naprogramovateľné riešenie v čase $O(n \cdot log n)$ (v C++ za použitia STL). Jeho anglický popis je tu.

3. K úlohe 1414z o aritmetickej postupnosti prvočísel: V roku 2004 Green a Tao dokázali, že musí existovať ľubovoľne dlhá takáto postupnosť (ale bez návodu, ako nejakú nájsť). Najdlhšia v auguste 2007 známa postupnosť má $24$ členov, prvý z nich je $468395662504823$ a diferencia $205619 \cdot 23\#$. ($23\# = 223092870$ je súčin prvočísel po $23$ vrátane).

   Update:

   17. mája 2008 našli Raanan Chermoni & Jaroslaw Wroblewski postupnosť dĺžky 25, hodnoty sú $6171054912832631 + 366384 \cdot 23 \# \cdot n$, pre $n=0$ až $24$.

4. V úlohe 1342 existuje elegantné (aj keď pomerne komplikované) lineárne riešenie, ktoré vyzerá nasledovne : Uvažujme najskôr špeciálnu situáciu, kedy $n=\frac{3k+1}{2}$. Očíslujme si pozície v poli od $0$ po $2n-1$. Knihy na pozíciách $0$ a $2n-1$ sú na správnom mieste. Pre ostatné knihy zjavne platí, že kniha, ktorá začína na pozícii $x$, chce skončiť na pozícii $2x \mod 2n-1$.

   Môžeme teda začať tým, že knihu z pozície $1$ dáme na pozíciu $2$, knihu odtiaľ na pozíciu $4$, atď., až kým nedostaneme opäť nejakú knihu na pozíciu $1$. Teraz využijeme našu vhodnú voľbu $n$. Pre naše $n$ platí, že $2n-1=3k$, no a $3k$ má tú vlasnosť, že sa v postupnosti hodnôt $2r \mod 3k$ (pre $r=0,1,\dots$) vyskytnú práve všetky čísla menšie ako $3k$, ktoré nie sú deliteľné $3$.

   Keď teda umiestnime knihu na pozíciu $1$, presunuli sme už práve všetky knihy, ktoré sú na pozíciách nedeliteľných $3$. Ostatné knihy presunieme podobne: Zopakujeme ešte niekoľkokrát ten istý proces, len namiesto začiatku na pozícii $1$ postupne začneme na pozíciách $3$, $32$, atď.

   Pre všeobecné n teraz lineárne riešenie zostrojíme nasledovne: Nájdeme najväčšie $k$ také, že $n \geq \frac{3k+1}{2}$. V lineárnom čase zrotujeme časť poľa, aby sme dostali v poli postupne prvé a druhé diely prvých $\frac{3k+1}{2}$ kníh, a za tým prvé a druhé diely ostatných kníh. Vyššie uvedeným postupom preusporiadame prvú časť, a následne sa rekurzívne zavoláme na druhú časť poľa.

   

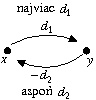
5. V riešení úlohy 1533 druhý odstavec: Rozmyslite si, že ak v našom grafe existuje cesta z $x$ do $y$ (pre $x<y$) so súčtom ohodnotení hrán $d$, znamená to, že z nerovníc zodpovedajúcich jednotlivým hranám vieme odvodiť tvrdenie: "v úseku od osady $x+1$ po osadu $y$ vrátane sa urodilo najviac $d$ plodov". Podobne, ak v grafe existuje cesta z $y$ do $x$, v úseku sa urodilo aspoň $-d$ plodov.

6. V úlohe 1543 nejde o úplne priamočiare použitie maximálneho toku, je potrebné upraviť graf tak, aby sme vedeli obmedziť kapacitu každého vrchola na $1$. Štandardná technika ako to dosiahnuť: V prvom kroku nahradíme každú neorientovanú hranu dvoma orientovanými. V druhom kroku "rozdelíme" každý vrchol na dva: "vstupný" vrchol, do ktorého budú vchádzať všetky prichádzajúce hrany, a "výstupný" vrchol, z ktorého budú vychádzať všetky odchádzajúce. V treťom kroku pridáme z každého vstupného vrchola hranu s kapacitou $1$ do jemu zodpovedajúceho výstupného vrchola.

7. V úlohe 1314 existuje aj lepšie riešenie v $O(p \cdot log p)$, pri ktorom nezostrojujeme celý graf, ale len tie jeho hrany, ktoré zodpovedajú hranám Delaunayovej triangulácie danej množiny bodov.