7. Osamelý a jednobunkový

Bol raz jeden jednobunkový organizmus menom Cecil¹. Bolo mu smutno, lebo nebolo nikoho, s kým by sa mohol porozprávať pri jedle, a tak sa Cecil začal deliť, aby mal koho pozvať na svoje párty.

Časom mal Cecil dosť potomkov, a tak sa rozhodol zorganizovať párty. Pozval na ňu všetkých svojich \(k\)-potomkov. (\(1\)-potomok Cecila je každé jeho dieťa, \(2\)-potomok je každé jeho vnúča, atď.)

Postupom času začali aj potomkovia Cecila organizovať párty podobným spôsobom. Každému svojmu \(k\)-potomkovi pošlú pozvánku na svoju párty. Tá má nasledovnú formu: “Na jeho veľkú párty ťa pozýva tvoj \(k\)-ty predok, sám magnificentný…”

Cecilovi potomkovia sú ale inteligentní, lebo to bolo v Cecilovych génoch. Je im jasné, že množstvo jedla a kofoly, ktoré sa im na párty ujde, je určené počtom účastníkov párty. Nie vždy sa teda oplatí ísť na párty. Pomôžte im pri rozhodovaní – pre každú pozvánku určite, koľko účastníkov bude na párty ak sa jej všetci pozvaní zúčastnia.

Úloha

Zadaný je zakorenený strom s \(n\) vrcholmi. Prichádza vám postupne \(m\) otázok. Každá otázka je určená vrcholom \(v\) a poradovým číslom predka \(k\). Pre každú otázku zistite, koľko \(k\)-potomkov má \(k\)-predok vrchola \(v\). Ak \(k\)-predok vrcholu \(v\) neexistuje, tak je odpoveď \(0\).

\(1\)-potomok vrcholu \(v\) je ľubovoľné jeho dieťa. Pre \(k > 1\) je \(k\)-potomok vrcholu \(v\) ľubovoľné dieťa niektorého \((k-1)\)-potomka \(v\). \(1\)-predok vrcholu \(v\) je otec \(v\) ak existuje. Pre \(k > 1\) je \(k\)-predok vrcholu \(v\) otec \((k-1)\)-predka \(v\).

Úlohu je nutné riešiť online – váš program sa nedozvie ďalšiu otázku, kým neodpovie na tú aktuálnu. Za každou odpoveďou preto použite fflush(stdio) alebo cout << flush, aby sa výstup vášho programu hneď odoslal testovaču.

Formát vstupu

Na prvom riadku vstupu je celé číslo \(t\) (\(1 \leq t \leq 1\,000\)) – počet testov. Každý z testov má nasledovný formát:

Prvý riadok testu obsahuje jedno celé číslo \(n\) (\(1 \leq n \leq 100\,000\)) – počet vrcholov stromu. Druhý riadok testu obsahuje \(n\) čísel \(p_1, p_2, \ldots, p_n\) – \(i\)-te z nich je číslo priameho predka vrcholu \(i\). Ak je vrchol \(i\) koreňom stromu, tak \(p_i = 0\). (Pre \(i\) také, že vrchol \(i\) nie je koreňom stromu platí \(1 \leq p_i \leq n\).) Môžete predpokladať, že zadaný graf je naozaj strom.

Tretí riadok testu obsahuje jedno celé číslo \(m\) (\(1 \leq m \leq 100\,000\)) – počet otázok. Nasleduje \(m\) riadkov, \(i\)-ty z nich obsahuje dve celé čísla \(v_i, k_i\) (\(1 \leq v_i, k_i \leq n\)) popisujúce otázku.

Súčet \(n\) zo všetkých testov nepresiahne \(100\,000\), a súčet \(m\) zo všetkých testov nepresiahne \(150\,000\).

Formát výstupu

Pre každú otázku vypíšte na samostatný riadok jedno celé číslo – počet \(k\)-potomkov \(k\)-predka vrcholu \(v\).

Príklad

Input:

2
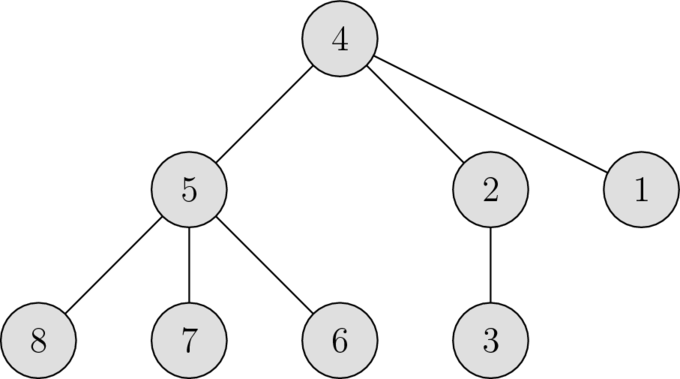
8
4 4 2 0 4 5 5 5
6
1 1 // 1-predok 1 je 4.
    // Jeho 1-potomkovia su 5, 2 a 1.
1 2 // 2-predok 1 neexistuje.
3 1 // 1-predok 3 je 2.
    // Jeho 1-potomok je len 3.
3 2 // 2-predok 3 je 4.
    // Jeho 2-potomkovia su 8, 7, 6 a 3.
3 3 // 3-predok 3 neexistuje.
5 1 // 1-predok 5 je 4.
    // Jeho 1-potomkovia su 5, 2 a 1.
5
3 0 2 5 1
5
4 5
4 1
1 2
1 3
2 1

Output:

3
0
1
4
0
3
0
1
1
0
0

Text uvedený za // je komentár – v skutočných vstupoch sa žiadne komentáre samozrejme nachádzať nebudú. Druhý test má správny formát. Strom v prvom teste vyzerá nasledovne: