Zadanie
Učiteľ chémie sa rozhodol, že dá hneď na začiatku školského roka písomku. Písať písomku až po tom ako sa preberie učivo, to by bolo príliš ľahké. Tiež by bolo príliš ľahké, keby mohli žiaci počas písomky od seba odpisovať.
Zistite, koľko najviac detí je možné umiestniť do triedy, tak aby si navzájom nevideli do zošitov. A aby ste to ani vy nemali príliš ľahké, niektoré stoličky sú pokazené a nedá sa na nich sedieť.
Úloha
V triede je \(m\) radov po \(n\) stoličiek, z ktorých niektoré sú pokazené. Každý žiak alebo žiačka musí sedieť na dobrej stoličke tak, aby na susedných stoličkách naľavo, napravo, vpredu vľavo a vpredu vpravo nesedel nikto iný.
Na obrázku je znázornené, že pre dané dieťa nemôže sedieť nikto iný na políčkach \(A\),\(C\),\(D\) ani \(F\). Všimnite si, že priamo pred dieťaťom (políčko \(B\)) môže byť obsadené.
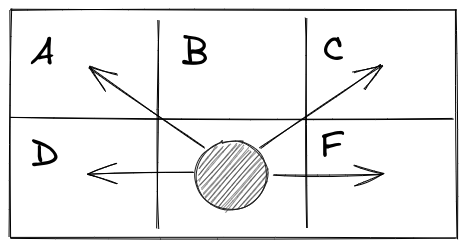
Vypočítajte a vypíšte, koľko najviac detí môže v danej triede sedieť.
Formát vstupu
V prvom riadku vstupu sú celé čísla \(m\) a \(n\) (\(1 \leq m,n \leq 200\)) udávajúce počet radov v triede a počeť stoličiek v jednom rade.
Nasleduje \(m\) riadkov po \(n\) znakov popisujúci triedu. Znak
'.' zodpovedá dobrej stoličke a znak 'x'
pokazenej stoličke.
| Sada | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| \(1 \leq m \leq\) | 4 | 4 | 10 | 10 | 20 | 40 | 80 | 200 |
| \(1 \leq n \leq\) | 4 | 80 | 10 | 80 | 20 | 40 | 80 | 200 |
Formát výstupu
Na výstup vypíšte jeden riadok obsahujúci jedno číslo – maximálny počet detí, ktoré môžu v triede sedieť.
Príklady
Input:
2 3
...
...Output:
4Input:
2 3
x.x
x.xOutput:
2Input:
10 10
....x.....
..........
..........
..x.......
..........
x...x.x...
.........x
...x......
........x.
.x...x....Output:
46Trocha netradične si najprv popíšeme vzorové riešenie a až potom pomalšie riešenie. Pomalšie riešenie navyše funguje aj na všeobecnejšiu úlohu, takže aj keď už viete vzorák, môže byť pre vás stále zaujímavé.
Vzorové riešenie
Máme popísané nejaké pravidlo, ktoré vraví že nemôže byť zároveň obsadená aj stolička \(A\) aj stolička \(B\), ak \(A\) a \(B\) sú v susedných stĺpcoch a v rovnakých alebo susedných radoch.
V zadaní je to napísane trocha inak, ale význam je rovnaký. A všimnime si, že formulácia v tomto odseku je viac očividne symetrická, ak vo vete vymeníme “A” a “B” tak sa nezmení význam. Symetria je dôležitá, pretože, keď si triedu pred predstavíme ako graf – dobré stoličky sú vrcholy grafu a susedné stoličky, ktorých obsadenie sa navzájom vylučuje, sú hrany grafu – tak dostaneme jednoduchý neorientovaný graf.
Druhá dôležitá vec je, že tento graf je bipartitný (“jáááj”, počujeme ozývať sa vzdychy riešiteľov, ktorým práve napadlo riešenie.). Bipartitný graf je taký, ktorý nemá cyklus nepárnej dĺžky.
No a zistiť, koľko najviac detí vieme usadiť do triedy je ekvivalentné tomu, koľko najviac vrcholov v grafe vieme ofarbiť zelenou farbou tak, aby žiadne dva susedné vrcholy neboli ofarbené (zelené vrcholy = obsadené stoličky). Ešte trochu formálnejšie napísané, chceme vybrať najväčšiu množinu vrcholov \(S\) tak, aby žiadne dva vrcholy v \(S\) neboli susedné.
Toto je už známy grafový problém, ktorý sa volá “Najväčšia nezávislá množina”, a ktorý sa v bipartitných grafoch rieši pomerne ľahko.
Vzorové riešenie tohto problému nájdete v našej kuchárke, najskôr sa potrebujete prehrýzť cez “Maximálne párenie v bipartitnom grafe” a z neho sa dá potom spočítať aj najväčšia nezávislá množina. Všetko je tam pekne popísané, ja osobne najviac odporúčam Hopcroftov-Karpov algoritmus, lebo má veľmi jednoduchú a efektívnu implementáciu, keď viete ako na to (ak neviete, pozrite kód nižšie).
Vo všeobecnosti má tento algoritmus časovú zložitosť \(O(E \sqrt{V})\), kde \(E\) je počet hrán a \(V\) počet vrcholov. V našom prípade máme \(O(mn)\) hrán a \(O(mn)\) vrcholov, takže zložitosť je \(O((mn)^{1.5})\). Pamäťová zložitosť je \(O(mn)\).
import sys
sys.setrecursionlimit(40234)
m, n = [int(x) for x in input().split()]
grid = [input() for _ in range(m)]
pair = [[None for _ in range(n)] for _ in range(m)]
# Returns True if found an augmenting path from (i, j)
# and updates the matching if such path was found
def find_improvement(i: int, j: int) -> bool:
visited[i][j] = True # only needed for calculating max_IS
for ii in (i - 1, i, i + 1):
for jj in (j - 1, j + 1):
if (
0 <= ii < m
and 0 <= jj < n
and grid[ii][jj] == "."
and not visited[ii][jj]
):
visited[ii][jj] = True
if pair[ii][jj] is None:
pair[ii][jj] = (i, j)
pair[i][j] = (ii, jj)
return True
else:
mi, mj = pair[ii][jj]
if find_improvement(mi, mj):
pair[ii][jj] = (i, j)
pair[i][j] = (ii, jj)
return True
return False
# Find maximum matching using Simplified Hopcroft-Karp.
# In each round we find "maximal disjoint set of augmenting paths".
# Note the set does not need to be maximum in size.
improved = True
while improved:
improved = False
visited = [[0 for _ in range(n)] for _ in range(m)]
for i in range(m):
for j in range(0, n, 2):
if grid[i][j] == "." and pair[i][j] is None:
if find_improvement(i, j):
improved = True
# Conveniently the last matching pass, found all visited vertices needed to calculate max_IS
max_is = 0
for i in range(m):
for j in range(n):
if grid[i][j] == ".":
max_is += (j % 2) ^ visited[i][j]
print(max_is)Pomalšie riešenie – dynamické programovanie
Ale čo mám ja robiť, keď som nikdy nepočul o bipartitných grafoch a nezávislých množinách? V tejto časti si ukážeme pomalšie riešenie, ktoré neuvažuje probléme ako o grafe a navyše by fungovalo, aj keby daný graf nebol bipartitný. (Napríklad, keby sa nebolo možné sedieť vedľa nikoho vo všetkých ôsmych smeroch, alebo keby iba nebolo možné sedieť na pozícii \((x, y)\), ak je obsadené ľubovoľné z políčok \(\{(x-1, y-1), (x-1, y-2), (x, y-3)\}\).)
Dalo by sa začať obyčajným bruteforcom, postupne prechádzame políčka po stĺpcoch. Ak sa na dané políčko nedá posadiť (lebo je pokazené, alebo je obsadené niektoré z ľavých susedov) musíme nechať políčko voľné, v opačnom prípade vyskúšame obe možnosti obsadenia. Toto riešenie by v najhoršom prípade skúšalo dokopy \(2^{mn}\) možností, ale dokážeme ho zlepšiť memoizáciou či prerobením na dynamické programovanie.
Kľúčové pozorovanie je, že keď už sme spracovali \(k\) políčok, obsadenosť políčok \([0..k-m)\) už nebude ovplyvňovať, ktoré budúce políčka môžeme alebo nemôžeme obsadiť neskôr.
Len pre ilustráciu si predstavme, že máme triedu s \(m=5\) radmi:
?????????A--------
????????AA--------
????????A---------
????????A---------
????????A---------Keď sme spracovali prvých 47 políčok (označené ? a
A), tak políčka označené ? už nezasahujú do
toho, kto môže sedieť na políčkach označených -.
Ak sa chceme posunúť v dynamickom programovaní o políčko ďalej, viď
druhý obrázok, vyskúšame všetkých \(2^{m+1}\) možností, ako môžu vyzerať
políčka B.
?????????B--------
?????????B--------
????????BB--------
????????B---------
????????B---------Na odpovedanie otázky “Koľko najviac detí môžeme usadiť na prvých \(k+1\) políčok ak zároveň obsadenie posledných \(m+1\) políčok zodpovedá binárnemu reťazcu \(B\)?” nám stačí poznať už spočítané odpovede pre \(k\) políčok a všetky možné binárne reťazce \(A\) dĺžky \(m+1\).
Domyslenie detailov necháme na čitateľa ako cvičenie, pri implementácii použijeme bitové operácie na efektívnu prácu s binárnymi reťazcami.
Celková časová zložitosť riešenia je \(O(2^m mn)\), pamäťová zložitosť je \(O(2^m)\), lebo si stačí pamätať len posledné dve vrstvy (\(k\) a \(k+1\)) tabuľky dynamického programovania.
#include <bits/stdc++.h>
using namespace std;
int main() {
int m, n;
cin >> m >> n;
vector<string> trieda(m);
for (int i = 0; i < m; i++) cin >> trieda[i];
int m2 = 1 << (m + 1);
vector<int> ans(m2, 0);
for (int j = 0; j < n; j++)
for (int i = 0; i < m; i++) {
vector<int> newans(m2, 0);
int check = 1 << (m - 1);
if (i != 0) check |= 1 << m;
if (i != m - 1) check |= 1 << (m - 2);
bool free = trieda[i][j] == '.';
for (int k = 0; k < m2; k++) {
int shifted = (k << 1) & (m2 - 1);
newans[shifted] = max(newans[shifted], ans[k]);
if (free && !(k & check)) {
newans[shifted + 1] = max(newans[shifted + 1], ans[k] + 1);
}
}
ans = move(newans);
}
int best = 0;
for (int x : ans) best = max(best, x);
cout << best << "\n";
}Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.