Zadanie
Viki nosí rôzne kusy oblečenia, ktoré majú veľa záhybov. A na čo sú dobré záhyby? Tam sa predsa plošticiam dobre schováva. Ploštica Cyprián takto raz naskočil na Viki a prešiel dokola po celom jej Kabáte, aby našiel všetky záhyby. Cyprián je iba ploštica, takže nevníma tretí rozmer a svoju trasu si vie zakresliť na papier. Ciprián navyše ide stále dopredu, až kým sa nevráti na pôvodné miesto. Zvládne si prí tom zapisovať iba to, aké kroky robí. Teda, či ide rovno, alebo sa otáča doprava, alebo doľava. Teraz by potreboval vašu pomoc, aby zistil, koľko miesta je v záhyboch.
Úloha
Na vstupe dostanete popis Cypriánovej trasy. Táto trasa sa nikde nepretína (nekrižuje samú seba) a končí tam, kde začala. Vašou úlohou je zistiť, koľko miesta je v záhyboch. Záhyb je každá obdĺžniková oblasť, ktorá je aspoň z dvoch protiľahlých strán ohraničená trasou (teda napríklad hore a aj dole).
Na nasledovnom obrázku sú miesta v záhyboch vyznačené sivou.

Formát vstupu
Na jedinom riadku vstupu sa nachádza reťazec písmen R L P ktoré postupne znamenajú rovno, doľava, doprava.
Dĺžka reťazca nepresiahne \(10^5\). Ak si počiatočnú pozíciu označíme ako \((0,0)\) tak súradnice bodov na trase v absolútnej hodnote nepresiahnu \(3\,000\). V reťazci sa nikdy nanachádzajú za sebou dve otočenia (teda L alebo P).
Formát výstupu
Vypíš jeden riadok a v ňom jedno celé číslo – celkovú plochu záhybov.
Príklady
Input:
RRRPRRRPRRRPRRRPOutput:
0Trasa na vstupe vyzerá ako štvorec.
Input:
RRRRRRPRRRRPRRPRRLRRLRRRPRRPRRRRROutput:
4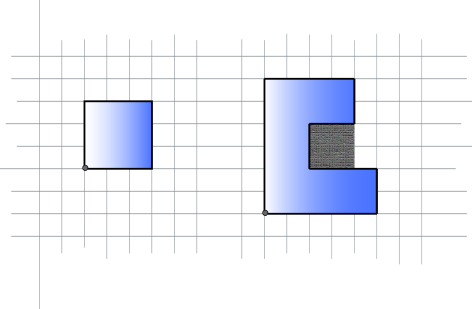
Na vyriešenie tejto úlohy bolo potrebné zistiť, kolko štvorčekov sa nachádza “v záhyboch”. Existuje na to viacero spôsobov. Jeden z nich je zistiť obsah útvaru na vstupe, potom ho akosi obaliť z vonka, zistiť obsah vrátane záhybov a vypísať ich rozdiel. My si ale ukážeme implementačne jednoduchšie riešenie.
Vstup
Prvá vec, ktorú musíme spraviť asi pri ľubovolnom riešení tejto úlohy, je rozumne načítať vstup. Potrebujeme nejakým spôsobom preložiť reťazec na čísla, teda súradnice. Dobrý spôsob je začať na súradniciach 5000, 5000, aby bolo všetko kladné, a potom si len pamätať aktuálnu pozíciu a smer, a podla vstupu updatovať a ukladať.
Hladanie záhybov
Aby sme si úlohu zjednodušili, predstavme si, že políčko je v záhybe, iba ak je ohraničené z hora a z dola. S takouto zmenou môžeme potom vstup spracovať po stĺpcoch, nezávysle na sebe. V každom stĺpci si zoradíme horizontálne pohyby od hora dole a následne iba prejdeme tento zoznam. Prvý pohyb znamená vonkajšiu hranicu, teda začína ohraničenú oblasť. Druhý prechod musí teda ukončovať ohraničenú oblasť, čiže začína záhyb. Tretí zase ukončuje záhyb a tak ďalej až po posledný. Prechodov je určite párny počet, lebo rovnako veľa smeruje doprava, ako do ľava. Každá ohraničená oblasť je teda aj z dola uzavretá.
Takýmto spôsobom vieme identifikovať políčka, ktoré sú vertikálnym smerom v záhyboch. Ak rovnaký postup zopakujeme po riadkoch, nájdeme všetky políčka v záhyboch.
Opakujúce sa políčka
Jediný problém tohoto riešenia je, že niektoré políčka zarátame dvojmo - aj pre riadok, aj pre stĺpec. Vzhľadom na veľkosť vstupu toto môžeme vyriešiť jednoducho tak, že si jednotlivé políčka (ich súradníce), vložíme do setu a už len vypíšeme veľkosť tohoto setu. V prípade jazykov, ktoré rýchlo pracujú s poľami, stačí tieto súradnice vyznačovať v dvojrozmernom poli a na konci spočítať.
Časová a pamäťová zložitosť
Dĺžka vstupného reťazca \(n\) nám v tomto prípade až tak veľa nehovorí, no pri najmenšom ho musíme načítať. Zadanie nám však dáva oveľa menšie ohraničenie, a to na veľkosť súradníc \(m\). Do celkovej časovej zložitosti teda započítame \(O(n)\) za načítanie vstupu a pri najhoršom \(O(m^2)\) za prechádzanie mriežky po riadkoch a stĺpcoch. Spolu je to teda \(O(n+m^2)\) za predpokladu, že ak použijeme set, tak je to hash-set a predpokladáme, že má konštantné operácie.
Pamäťovú zložitosť môžeme odhadnúť rovnako, pretože si ukladáme pretransformovaný vstup, ktorý je v princípe rovnako veľký ako pôvodný a tiež si ukladáme všetky políčka, ktoré sú v záhyboch, čo je najviac \(O(m^2)\).
from collections import defaultdict
dir = [[1,0], [0,1], [-1,0], [0,-1]]
ver = defaultdict(list)
hor = defaultdict(list)
x = 5000
y = 5000
nd = 0
s = input()
for j in s:
if j == 'P': nd = (nd + 1) & 3
elif j == 'L' : nd = (nd + 3) & 3
elif j == 'R' :
nx = x + dir[nd][0]
ny = y + dir[nd][1]
if (y != ny):
hor[min(y, ny)].append(x)
else:
ver[min(x, nx)].append(y)
x = nx
y = ny
policka = set()
for i in ver.keys():
ver[i].sort()
for i in hor.keys():
hor[i].sort()
for x in ver.keys():
j = 1
while j + 1 < len(ver[x]):
y1 = ver[x][j]
y2 = ver[x][j+1]
for y in range(y1, y2):
policka.add((x,y))
j+=2
for y in hor.keys():
j = 1
while j + 1 < len(hor[y]):
x1 = hor[y][j]
x2 = hor[y][j+1]
for x in range(x1, x2):
policka.add((x,y))
j+=2
print(len(policka))#include <iostream>
#include <set>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;
const int dir[4][2] = {{1,0}, {0,1}, {-1,0}, {0,-1}};
vector<int> ver[10000], hor[10000];
int main(){
int x = 5000, y = 5000, nd = 0;
for (int i = 0; i < 10000; i++)
ver[i].clear(), hor[i].clear();
char s[70000];
int t;
scanf("%s", s);
for (int j = 0; j < strlen(s); j++)
{
int nx, ny;
switch (s[j])
{
case 'P' : nd = (nd + 1) & 3; break;
case 'L' : nd = (nd + 3) & 3; break;
case 'R' :
nx = x + dir[nd][0], ny = y + dir[nd][1];
if (y != ny)
hor[min(y, ny)].push_back(x);
else
ver[min(x, nx)].push_back(y);
x = nx, y = ny;
break;
}
}
set<int> policka[10000];
for (int i = 0; i < 10000; i++)
sort(ver[i].begin(), ver[i].end()), sort(hor[i].begin(), hor[i].end());
for (int x = 0; x < 10000; x++)
for (int j = 1; j + 1 < ver[x].size(); j+=2)
{
int y1 = ver[x][j], y2 = ver[x][j+1];
for (int y = y1; y < y2; y++)
policka[x].insert(y);
}
for (int y = 0; y < 10000; y++)
for (int j = 1; j + 1 < hor[y].size(); j+=2)
{
int x1 = hor[y][j], x2 = hor[y][j+1];
for (int x = x1; x < x2; x++)
policka[x].insert(y);
}
int ret = 0;
for (int i = 0; i < 10000; i++)
ret += policka[i].size();
printf("%d\n", ret);
return 0;
}Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.