5. Taktická záchrana vzorové riešenie

>>> 1
>>> 3
<<< ? 1 1
>>> 1
<<< ? 1 2
>>> 2
<<< ? 1 3
>>> 4
<<< ! 6 5 3

Prvé technické detaily

Pred tým, ako sa pustíme do riešenia úlohy, pozrime sa na to, ako si reprezentujeme druhy ploštíc v posteliach a ako s touto reprezentáciou pracovať.

V zadaní sú ploštice v nejakej posteli reprezentované cez celé čísla - presnejšie cez ich binárny zápis. Ak čísla \(a\) a \(b\) reprezentujú ploštice v dvoch posteliach. Farby, ktoré sa nachádzajú na niektorej z nich, sa dajú zistiť pomocou binárneho ORu – a to ako a | b (aj v pythone aj v C++). Táto operácia vráti číslo ktoré má na \(i\)-tom bite jednotku práve vtedy, ak má aspoň jedno z čísel \(a\) a \(b\) na \(i\)-tom bite jednotku.

Jednoduché riešenie

Vybavený potrebnou mechanikou, poďme sa pustiť do riešenia úlohy. Ak vieme stav každej postele, vieme zistiť pre každú posteľ, aké farby ploštíc sa zachránia, ak práve táto bude napadnutá – jednoducho si vypočítame OR ostatných postelí. Takto vieme odpovedať na jednu testovaciu sadu pomocou \(n\) otázok v \(O(n^2)\) čase pomocou a \(O(n)\) pamäti. A tak vieme získať \(1\) bod.

Toto riešenie vieme zrýchliť pomocou OR-ekvivalentu prefixových a suffixových súčtov: prefixových a suffixových OR-ov. Vieme si v \(O(n)\) čase spočítať pre každé \(1\leq i\leq n\), aké farby ploštíc sú na posteliach \(1, 2, \dots, i - 1\) a aké farby ploštíc sú na posteliach \(n, n - 1, \dots, i + 1\) a následne vypísať OR týchto dvoch hodnôt (všimnite si, že na vypočítanie prvej hodnoty pre pozíciu \(i\) z hodnoty pre pozíciu \(i-1\) stačí konštantný čas a nápodobne pre druhú hodnotu z hodnoty pre \(i+1\)).

Menej otázok: pokrývame postele

Na viac bodov sa musíme vedieť nespýtať na každú posteľ separátne. Ako na to?

Položme si otázku inak. Pre aké otázky vieme vyskladať odpoveď?

Predstavme si, že sa spýtame na \(k\) množín postelí. Označme ich ako \(S_1,\dots, S_k\) a dostaneme odpovede \(a_1, \dots, a_k\). Kedy vieme zistiť z týchto otázok informáciu “aké farby ploštíc ostanú, ak bude prvá zasiahnutá posteľ \(i\)”? Nemôžeme použiť informácie zo žiadnej množiny ktorá obsahuje \(i\) - inak nevieme, či farba ploštíc je na posteli \(i\) alebo aj na inej posteli z množiny. Pozrime sa teda na všetky množiny neobsahujúce \(i\). Ak je každá iná posteľ (okrem \(i\)) obsiahnutá v niektorej z týchto množín, všetky jej farby ploštíc budú obsiahnuté v OR-e odpovedí pre tieto postele.

Takže dostávame podmienku: na to aby sme vedeli odpovedať s pomocou otázok na množiny \(S_1, \dots, S_k\), musí pre každý pár rôznych postelí \(i\neq j\) existovať množina, v ktorej nie je posteľ číslo \(i\), ale nachádza sa v nej posteľ \(j\).

Ako ale takúto množinu skonštruovať?

\(n/2 + 2\) otázok

Hint, ako vyriešiť úlohu na dva body je v počte otázok: \(n / 2\) naznačuje, že by sme si mohli rozdeliť postele na dvojice – postele \(1, 2\), postele \(3, 4\), až \(n - 1, n\)¹ (na obrázku môžme vidieť rozdelenie pre \(n = 8\)). Takéto rozdeliene nám ale ešte úplne úlohu nevyrieši.

Pre každú z postelí, zjednotenie množín, ktoré ju neobsahujú, obsahujú všetky postele okrem jej dvojice. Chceli by sme teda pridať nejaké (najviac dve) množiny, pomôcou ktorých by sme vedeli “rozlíšiť” aj postele v jeden dvojici. Na to nám stačí si uvedomiť dve veci:

1. Je v poriadku, ak sú informácie o nejakej posteli “pridané dvakrát” (keďže nepočítame počet výskytov rôznych farieb, len či sú alebo nie sú)

2. V každej dvojici je jedna párna a jedna nepárna posteľ

Teda nám stačí sa navyše spýtať na množinu všetkých párnych a na množinu všetkých nepárnych postelí (ako môžme vidieť na obrázku dole pre \(n = 8\)).

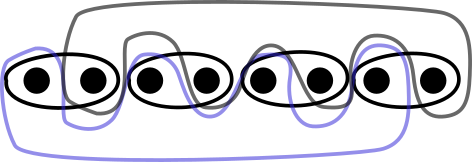
Vieme ľahko skontrolovať, že táto voľba množín spĺňa horeuvedenú podmienku: pre každé dve rôzne postele - buď nenasledujú priamo za sebou (a teda nie sú v rovnakej dvojici) alebo majú rozličnú paritu.

Skonštruovať odpoveď pre každú posteľ vieme pomocou \(n / 2\) otázok, a tak dostaneme časovú zložitosť \(O(n^2)\) a pamäťovú \(O(n)\).

Vieme zlepšiť toto riešenie?

V predchádzajúcom riešení sme rozdelili postele na po sebe idúce dvojice, a následne podľa zvyšku po delení dvoma. Ale číslo dva nie je v tomto prípade špeciálne! Mohli by sme nápodovne použiť trojice, štvorice, resp. akékoľvek \(k\)-tice. Rovnakou stratégiou ako pre dvojice, vieme získať pre \(k\)-tice odpoveď pomocou \(n / k + k\) otázok.

Ak sa s týmto výrazom pohráte, zistíte, že najmenej otázok (\(2\rceil\sqrt(n)\lceil\)) nám výjde pre \(k\) rovné \(\sqrt(n)\) (zaokrúhlené na najbližšie celé číslo). Takéto zlepšenie nám dá \(4\) body a zlepší časovú zložitosť na \(O(n\sqrt{n}))\) a pamäťovú na \(O(n)\).

Ešte menej otázok

Skupinkovaciu metódu sme už očividne zlepšili ako sa dalo, ale ešte stále nemám plný počet bodov. Mohli však by sme sa inšpirovať na lepšie riešenie?

Vráťme sa späť ku rozdeleniu postelí na dvojice. Toto rozdeľovanie je zjavne neefektívne, keďže potrebujeme lineárne množstvo množín, aby sme pokryli všetky postele. Čo keby sme sa v jednej množine spýtali na polovicu dvojíc a v druhej na druhú polovicu dvojíc. Takto stále očividne nevieme rozoznávať všetky postele. Odpoveďou je: rozdelenie dvojíc na polovice viacerými spôsobmi.

Limit \(2\log n\) v zadaní nám vie napríklad napovedať nasledovné množiny:

• všetky párne postele, všetky nepárne postele
• každá párna dvojica, každá nepárna dvojica
• každá párna štvorice, každá nepárna štvorica
• …
• prvá polovica postelí, druhá polovica postelí²

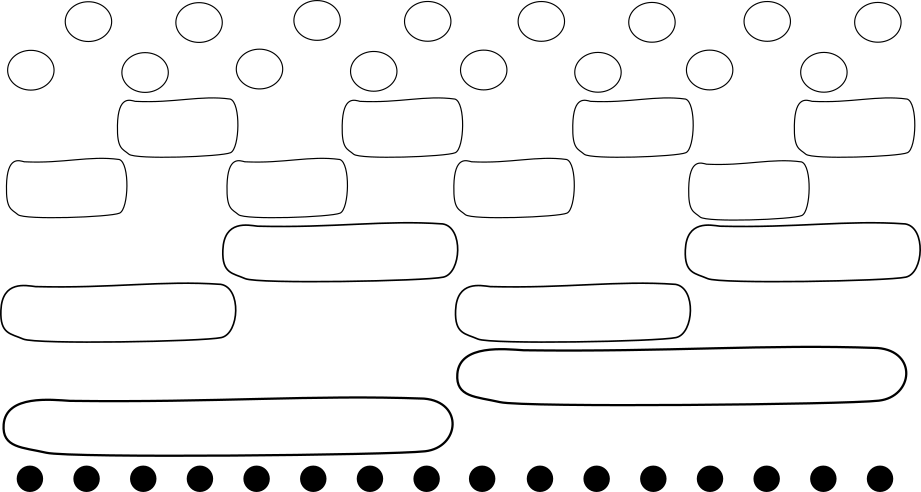
Na obrázku môžeme vidieť množiny pre \(n = 16\). Ako prvé si všimnime, že takto dostaneme \(2\lceil\log n\lceil\) otázok. Po druhé, tieto množiny nám vedia vyskladať všetky odpovede – predstavme si, že chceme odpoveď na \(i\)-tú posteľ (teda, ktoré farby sú na ostatných posteliach). Pozrime sa na binárny zápis čísla \(i\). Ten nám presne povie ktoré query máme skombinovať. Ak má \(i\)³ na \(j\)-tom bite \(1\), poto chceme použiť odpoveď pre párne \(2^i\)-tice a v opačnom prípade odpoveď pre nepárne \(2^i\)-tice. Keďže rôzne postele majú rôzne binárne zápisy a v každom “leveli” otázok sa každá posteľ nachádza v presne jednej z množín, vieme tak rozlišovať každú dvojicu postelí.

Takto dostaneme teda riešenie v časovej zložitosti \(O(n\log n)\) s pamäťou \(O(n)\), ktoré vie získať \(6\) bodov (pre \(n = 1000\) použije \(20\) otázok).

Vzorové riešenie

Narozdiel od predchádzajúcich riešení, vo vzorovom si množiny necháme vygenerovať programom, ale nie na základe jednoduchého vzoru.

Pozrime sa na množiny z pohľadu postelí: v ktorých množinách z \(k\) opýtanych množín sa bude nahádzať posteľ \(i\)?

Zjavne dáva zmysel, aby každá posteľ bola v približne rovnakom počte množín. V predchádzajúcom riešení bola každá posteľ v polovici množín, čo keby sme sa týmto princípom inšpirovali?

Vzorové riešenie potrebuje použiť najviac \(13\) množín, mohli by sme zariadiť aby každá posteľ bola v \(6\) z nich?

Existuje \(\binom{13}{6} = 1716\) rôznych spôsobov, akým je možné vybrať \(6\) z \(13\) množín, do ktorých nejaká posteľ bude patriť. Keďže to je menej, ako všetkých postelí, ktoré vieme na vstupe dostať, vieme pre každú vybrať unikátny výber množín, v ktorých bude zaradená. Takto teda vieme nájsť pre každú dvojicu postelí množinu, v ktorej prvá posteľ je a druhá nie je (keďže všetky postele sú v rovnakom počte množín).

Teda na dokončnie riešenia nám treba len vymyslieť ako ho implementovať – odporúčam použiť next_permutation v C++, alebo knižnicu itertools v pythone. Keď si množiny generujeme, vieme si rovno zapísať, ktorú množiny treba OR-ovať, aby sme získali výsledok pre tú-ktorú posteľ. Toto riešenie použije \(13\) otázok a vieme ho implementovať v čase a pamäti \(O(n)\).

V skutočnosti, ak by \(n\) nebolo horne ohraničená, potrebovali by sme rádovo \(\log n\) otázok – vieme ukázať, že menej než \(2\log n\) postačí, ale potrebujeme aspoň \(\log n\)⁴, takže časová zložitosť je v skutočnosti \(O(n\log n)\).

#!/usr/bin/env python3
import itertools, sys

def has_seven_ones(a):
    cnt = 0
    for i in range(13):
        if ((1 << i) & a) > 0:
            cnt += 1
    return (cnt == 7)

def solve():
    n = int(input())
    k = 0
    a = (1 << 7) - 1
    S = [[] for _ in range(13)]
    ktore = [[] for _ in range(n)]
    res = [0 for _ in range(13)]
    while k < n:
        if has_seven_ones(a):
            for i in range(13):
                if ((1 << i) & a) > 0:
                    S[i].append(k)
                else:
                    ktore[k].append(i)
            k += 1
        a += 1
    
    for i in range(13):
        print("? {} {}".format(len(S[i]), " ".join(map(lambda x: str(x + 1), S[i]))))
        sys.stdout.flush()
        res[i] = int(input())
    final = [0 for _ in range(n)]
    for i in range(n):
        for j in ktore[i]:
            final[i] |= res[j]
    print("! {}".format(" ".join(map(str, final))))
    
t = int(input())
for _ in range(t):
    solve()