8. A čo tak viac Torty? vzorové riešenie

8 9
VVTVTTVV
vysledok 1 5
vymen 1 T
vysledok 1 5
pridaj 2 V
vysledok 1 5
zmaz 5 6
vysledok 1 5
reverzni 1 4
vysledok 1 5

6
8
6
8
6

Poďme sa pozrieť, ako vieme postupne riešiť jednotlivé operácie, a tak prísť ku vzorovému riešeniu. Pre jednoduchosť si predstavme, že každé V nahradíme \(1\), a každé T nahradíme \(-1\), a takto z reťazca dostaneme postupnosť čísel, \(x_1,\dots,x_l\), kde \(l\) je aktuálna dĺžka postupnosti.

Výsledok

Zo vzorového riešenia Organizácie Kapustnice, vieme, že výsledok pre postupnosť \(x_1, \dots, x_l\) je

\[ l + V + \max\{\sum_{i=1}^l x_i + V, 0\} \]

kde \(V = -\min_{0\leq i\leq l}\{\sum_{j=1}^i x_j\}\) je najmenší súčet prefixu postupnosti, teda počet vedúcich, ktorý treba pridať na koniec stola.

Podobne, ak chceme vyriešiť úlohu pre podreťazec \(x_{i_z},x_{i_z + 1}, \dots, x_{i_k}\), vtedy sa nám vzorec jednoducho zmení na

\[ l + V + \max\{\sum_{i=i_z}^{i_k} x_i + V, 0\} \]

kde \[V = -\min_{i_z-1\leq i\leq i_k}\{\sum_{j=i_z}^{i_k} x_j\}\]

Prvá sada – malé vstupy

V prvej sade si vieme dovoliť spraviť každú operáciu v linárnom čase v závislosti od dĺžky reťazca. Každú query, ktorá nie je vysledok vieme vykonať v lineárnom čase, a rovnako tak vieme aj spočítať horeuvedený vzorec. Takto dostaneme riešenie so zložitosťou \(O(q(q+n))\) (keďže dĺžka reťazca nikdy nepresiahne \(q+n\)).

Druhá sada – pridávame na koniec

Ako si môžeme všimnúť, ak pridáme na koniec postupnosti novú hodnotu \(x_{l+1}\in\{1, -1\}\), vieme výsledok vypočítať v konštantnom čase – za predpokladu,, že si pamätáme pár údajov pre predchádzajúci reťazec. Menovite, ak si pamätáme

\[V_l = -\min_{i_z-1\leq i\leq i_k}\{\sum_{j=i_z}^{i_k} x_j\}\]

a

\[S_l = \sum_{i=1}^l x_i\]

Následne vieme tieto hodnoty updatnúť v konštantnom čase na

\[ S_{l+1} = S_l + x_{l+1} \]

a

\[ V_{l+1} = -\min\{-V_l, S_{l+1}\} \]

Z týchto hodnôt už vieme v konštatnom čase zistiť výsledok pre \(x_1 x_2 \dots x_l x_{l+1}\). Teda dostaneme riešenie v čase \(O(n+q)\), a pamäti \(O(n)\) riešiace druhú sadu.

Tretia sada – ľubovoľný podinterval

Pozrime sa teraz na tretiu sadu: máme nemenný reťazec, ale chceme vedieť vyriešiť úlohu na ľubovoľnom podintervale. Skúsenejší riešiteľ už v tomto vidí interval… čo znie ako intervaláč! A naozaj, napriek tomu, že namiesto priamočiareho minimového, alebo súčtového intervaláča, musíme vymyslieť niečo prefíkanejšie.

Chceli by sme si vedieť v intervaláči pamätať také hodnoty aby sme z nich vedeli zrekonštruovať

• súčet na danej podpostupnosti
• minimá prefixových súčtov v danej podpostupnosti

Prvú hodnotu vieme vypočítať jednoduchým súčtovým intervaláčom (pozri https://www.ksp.sk/kucharka/intervalovy_strom/). Čo s druhou hodnotou? Základná myšlienka je, že ak vieme súčet na nejakej podpostupnosti \(x_{i_1}\dots x_{i_2}\) (označme ho \(s\)), a taktiež navyše vieme minimá prefixových súčtov na podpostupnosti \(x_{i_1}\dots x_{i_2}\) a \(x_{i_2}+1, \dots, x_{i_3}\) (označme ich postupne \(v_1\) a \(v_2\)), potom minimum prefixových súčtov na podpostupnosti \(x_{i_1}, \dots, x_{i_2},\dots,x_{i_3}\) je minimum z \(v_1\) a \(v_2 + s\).

Na základe tejto myšlienky vieme následne skonštruovať intervalový strom, ktorý si okrem prefixových súčtov navyše pamätá v každom vrchole minimum prefixových súčtov na jeho podintervale – vypočítať tieto hodnoty si vieme rekurzívne, na základe horeuvedeného vzorca.

Výsledok na zadanom intervale vieme získať skombinovaním údajov z \(O(\log n)\) vrcholov stromu, tak ako v klasickom intervaláči. Takto teda získame riešenie pre tretiu sadu, ktoré beží v čase \(O(n+q\log n)\) a \(O(n)\) pamäti.

Pridávame vymeň

Toto intervaláčové riešenie vieme jednoducho vylepšiť, aby vedelo vyriešiť aj sady 4 a 5. V nich navyše pribúda operácia vymen. Všimnime si, že jej pridaním sa nám stále nezmení dĺžka postupnosti. Preto by sme mohli použiť horeuvedené riešenie, ak by sme do intervaláča vedeli implementovať aj query na menenie hodnôt v postupnosti. To je štandardná intervaláčová operácia, ktorú vieme dosiahnuť aj s naším intervaláčom: súčtovú časť intervaláča vieme updatnuť ako v klasickom súčtovom intervaláči, a hodnotu prefixových miním tiež meníme len na \(O(log n)\) vrcholoch ktoré idú z listu (kde je menená hodnota) do koreňa. Spočítame ju rovnakým rekurzívnym vzorčekom, ako keď sa počítali počiatočné hodnoty intervaláča.

Dostaneme teda riešenie riešiace sady 3, 4 a 5 bežiace v čase \(O(n+q\log n)\) a pamäti \(O(n)\).

Ďalšie sady – nastupuje treap

Problém s operáciami pridaj a zmaz je, že intervaláč má fixné poradie prvkov, a hoci by sme teoreticky vedeli doimplementovať odoberanie a pridávanie prvkov na konci poľa (zamyslite sa :)), problém je pridávanie/vymazanie prvku na/z ľubovoľného indexu. Mohli by sme nejako náš intervaláč zovšeobecniť?

Odpoveď je áno. Predstavme si, že by sme mali binárny strom, pre ktorý platí, že každý vrchol reprezentuje pozíciu v postupnosti (nazvime ju \(i\)), všetky vrcholy v jeho ľavom podstrome (ak existuje) sú pozície pred \(i\) a všetky pozície v pravom podstrome (ak existuje) sú za \(i\). Napríklad, pre vstup zo zadania by mohol strom vyzerať nasledovne.

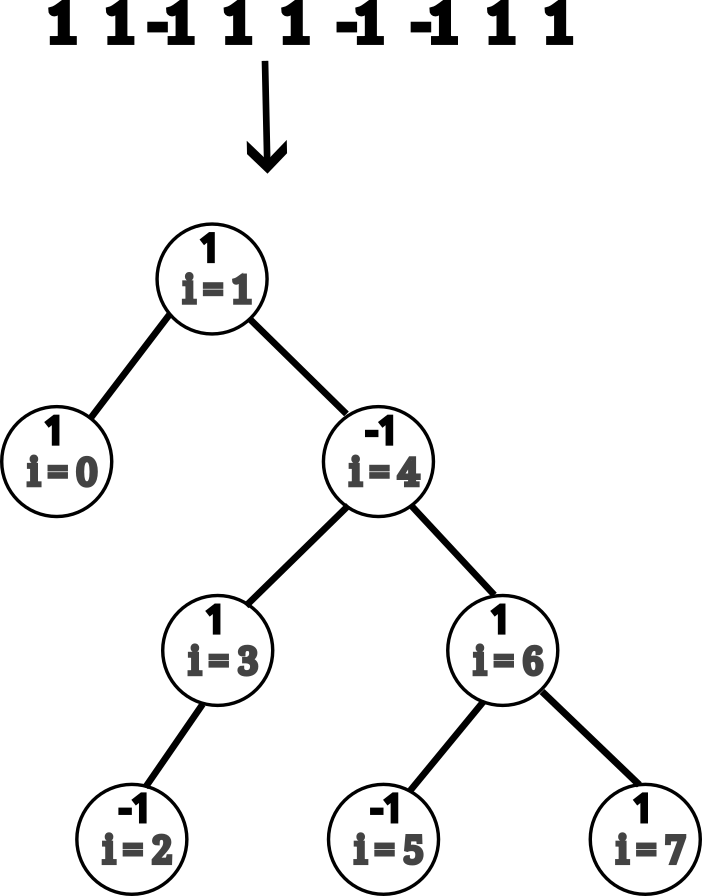
Všimnime si, že pre takýto strom vieme rovnako ako pre intervaláč vypočítať v každom vrchole hodnoty súčtu jeho intervalu a minimum prefixových súčtov na jeho intervale, a následne vieme zistiť hodnotu na nejakom v intervale v čase lineárnom od hĺbky stromu (podobne ako v intervaláči, rozmyslite si to).

Problém je práve s hĺbkou tohto stromu (a pridávaním a zmazaním). Potrebovali by sme taký strom, kde je hĺbka približne logaritmická a navyše vieme horeuvedené operácie vykonávať dostatočne rýchlo. Ako odpoveď nám príde treap.

Treap

Treap je, ako názov napovedá, strom (tree) aj https://www.ksp.sk/kucharka/halda/ (heap) zároveň. Predstavme si, že pre každú pozíciu si náhodne vygenerujeme jej prioritu, a v strome budeme udržiavať pravidlo, že v každom podstrome má najväčšiu prioritu jeho vrchol. Dá sa ukázať, že pre dané poradie vrcholov (ako v strome opísanom vyššie) a prioritu vrcholov, existuje práve jeden tvar, ktorý strom musí mať, a zároveň, ak priority vyberáme náhodne, bude hĺbka stromu \(O(\log V)\) kde \(V\) je počet vrcholov.

Mohli by sme sa teraz zastaviť a spýtať sa “počkať, ale prečo práve treap? Je to jediné riešenie?”, a odpoveď je: nie, ale je pomerne príjemný na implementáciu, ako môžete vidieť v https://www.ksp.sk/kucharka/treap/.

Môžete si všimnúť, že síce väčšina implementácií treapov ktoré nájdete (napríklad v kuchárke) používa treap ako binárny vyhľadávací strom, kde sú prvky zoradené od najmenšieho po najväčší. V našom prípade však prvky chceme mať zoradené podľa poradia v postupnosti. Na to však netreba robiť veľké zmeny. Stačí keď pri vyhľadávaní konkrétneho prvku sa algoritmus nebude rozhodovať na základe toho či je väčší ako \(x\) ale či je pred ním aspoň \(k\) prvkov.

Hlavné dve funkcie treapu (pomocou ktorých vieme už v princípe všetko ostatné potrebné implementovať), ako v kuchárke môžte vidieť sú split a merge. V https://www.ksp.sk/kucharka/treap/ nájdete ako tieto funkcie implementovať, ale my si tu v skratke opíšeme čo robia a ako ich použiť na implementáciu pridaj a zmaz.

Split

Prvou z nich je split, ktorá zoberie treap a číslo \(0 \leq k\) a vráti dva treapy: prvý obsahujúci prvých \(k\) pozícií vstupného treapu, a druhý obsahujúci ostatné pozície. (Na obrázku \(p\) označuje prioritu vrcholu.)

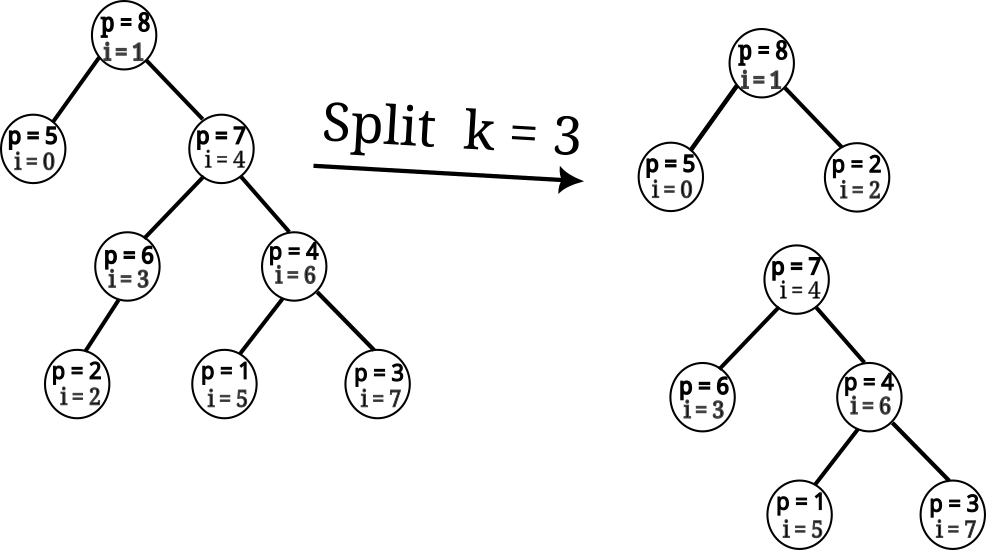
Split vieme naprogramovať jednoduchou rekurzívnou funkciou (ako tiež možno vidieť v kuchárke) zobrazenou na nasledovnom pseudokóde.

Split(T, k):
    Ak k = 0, vráť (prázdny treap, T)
    Ak veľkosť(T) je najviac $k$, vráť (T, prázdny treap)
    Ak veľkosť(T -> prvý syn) je najviac k
        T1, T2 je výsledok z Split(T -> prvý syn, k)
        Vymeň prvého syna stromu T za T2 a vráť (T1, modifikovaný T)
    Ak veľkosť(T -> prvý syn) je viac ako k,
        T1, T2 je výsledok z Split(T -> druhý syn, k - 1 - (veľkosť(T -> prvý syn))
        Vymeň druhého syna stromu T za T1 a vráť (modifikovaný T, T2)

Všimnime si, že si chceme okrem informácií o súčtoch a miním prefixových súčtov pre jednotlivé podstromy navyše udržovať informáciu o veľkostiach jednotlivých podstromov. Keďže pri funkcii split sa mení najviac “hĺbka stromu”¹ podstromov, a preto nám stačí tieto informácie (nápodobne ako pri intervaláči) zmeniť len raz v každej vrstve rekurzie funkcie.

Merge

Druhá funkcia na ktorej treap stojí je merge. Tá zoberie na vstupe dva treapy (reprezentujúce dve postupnosti) a vráti jeden treap reprezentujúci zreťazenie ich postupností. Príklad tejto operácie vidíme na nasledovnom obrázku.

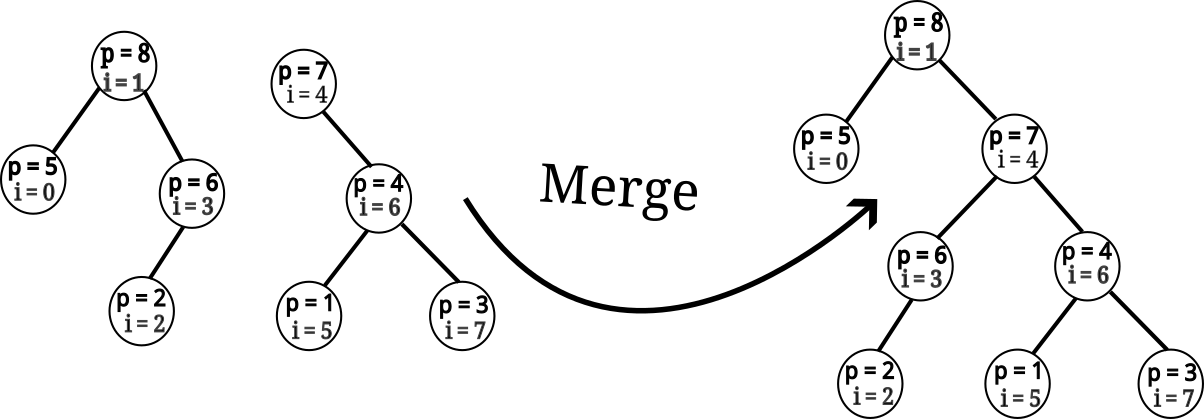
Vieme ju, podobne ako split naprogramovať pomocou jednoduchej rekurzívnej funkcie, ako vidíme na nasledovnom pseudokóde.

Merge(T1, T2)
    Ak T1 je prázdny treap, vráť T2. Ak je T2 prázdny treap, vráť T1.
    Ak priorita(T1) > priorita(T2)
        Vymeň druhého syna T1 za výsledok Merge(T1 -> druhý syn, T2) a vráť modifikovaný T1
    Inak, vymeň prvého syna T2 za výsledok Merge(T1, T2 -> prvý syn) a vráť modifikovaný T2

Všimnite si, že podobne ako pri split, aj počet rekurzívnych volaní pri merge nepresiahne hĺbky \(T1\) a \(T2\), a teda najviac toľkým podstromom treba aktualizovať hodnoty.

Ako to teda vyriešiť?

Poďme si to celé dať dokopy. Pre každý vrchol v treape si chceme pamätať nasledovné informácie:

• Priorita (náhodne vygenerovaná)
• Prvok postupnosti na pozícii odpovedajúcej vrcholu
• Veľkosť podstromu
• Súčet pozícií na intervale odpovedajúcom podstromu
• Minimum z prefixových súčtov na intervale odpovedajúcom podstromu

Vždy keď sa vrchol, alebo jeho synovia zmenia, updatneme posledné tri informácie (súčet a minimum vypočítame tak, ako v intervaláči).

Pozrime sa najskôr na to, ako do existujúceho treapu, označme to T, pridať prvok \(p\) na pozíciu \(i\). Stačí nám použiť split a merge, tak že si rozdelíme treap na prvky “pred” a “za” novopridaným prvkom, a následne pomocou mergu, už treap “zlepíme” dokopy spolu s novým prvkom. Môžeme to vidieť na nasledovnom pseudokóde:

T1, T2 = split(T, i)
T = merge(T1, merge(treap(p), T2))

kde treap(p) je jednoprvkový treap reprezentujúci postupnosť \(p\).

Zmazanie intervalu od \(z\) po \(k\) (vrátane) vieme implementovať podobne, tak že si najskôr rozbijeme treap na tri treapy – reprezentujúce pozície pred intervalom, pozície v intervale, a pozície za intervalom, a prvý a tretí zlepíme merge-om späť dokopy.

T1, T2 = split(T, z)
T2, T3 = split(T2, k - z + 1)
T = merge(T1, T3)

Aby sme nezabudli na query zmen, tú vieme implementovať buď cez skombinovanie zmaz a pridaj, alebo priamo rekurzívnou funkciou – podobne ako update v intervaláči, ktorú nechávame ako úlohu na zamyslenie.

No, a na koniec, keď dostaneme počiatočný reťazec, vieme z neho vytvoriť treap napríklad pomocou \(n\) operácií pridaj na koniec.

Časová zložitosť je \(O((n + q)\log (n + q))\)², a pamäť nám stačí \(O(n)\).

Plný počet bodov – nebojte sa lenivého treapu

V poslednej sade nám prišla posledná z operácií reverzni. Táto operácia vyzerá na prvý pohľad zákerne, ale našťastie, ukáže sa, že na ňu stačí treap a nemusíme vymýšľať divokejšie dátové štruktúry.

S predpokladom, že ideme upravovať nejaký treap, poďme sa najskôr zamyslieť, ako sa nám zmení výsledok pre nejaký interval, ak ho celý reverzneme. Ako sme si už predtým všimli, ak nejaký interval rozdelíme na podintervaly, ak vieme pre ne hodnoty súčtov a miním prefixových súčtov, vieme z toho poskladať výsledok na celom intervale. Konkrétne sa pozreme na jeho nový súčet a minimum prefixových súčtov.

Súčet, prirodzene, ostáva ten istý. Zato nové minimum prefixových súčtov bude minimum sufixových súčtov³. Síce ich nevieme spočítať priamo z minima prefixových súčtov, všimnite si, že podobne ako minimá prefixových súčtov, ich vieme “poskladať” zo súčtov, a miním sufixových súčtov pre postupnosť.

Konkrétne, ak vieme že postupnost \(x_{i_1}, \dots, x_{i_2}\) má súčet \(s_1\) a minimum sufixových súčtov \(S_1\), a postupnosť \(x_{i_2+1},\dots,x_{i_3}\) má súčet \(s_2\) a minimum sufixových súčtov \(S_2\), potom je minimum sufixových súčtov postupnost \(x_{i_1}, \dots x_{i_2}, x_{i_2+1}, \dots x_{i_3}\) rovné \(\min(S_2, s_2 + S_1)\).

Mohli by sme si teda v každom vrchole aj zapamätať minimum sufixových súčtov na príslušnom intervale.

Teraz vieme, ako sa nám mení výsledok pre obrátený interval, tak poďme sa zamyslieť nad tým, ako by sme mohli obrátiť (pre začiatok) celý treap. Pozrime sa na príklad reverzu. Pre prehľadnosť sme aj reverznutému stromu ponechali pôvodné indexy v postupnosti

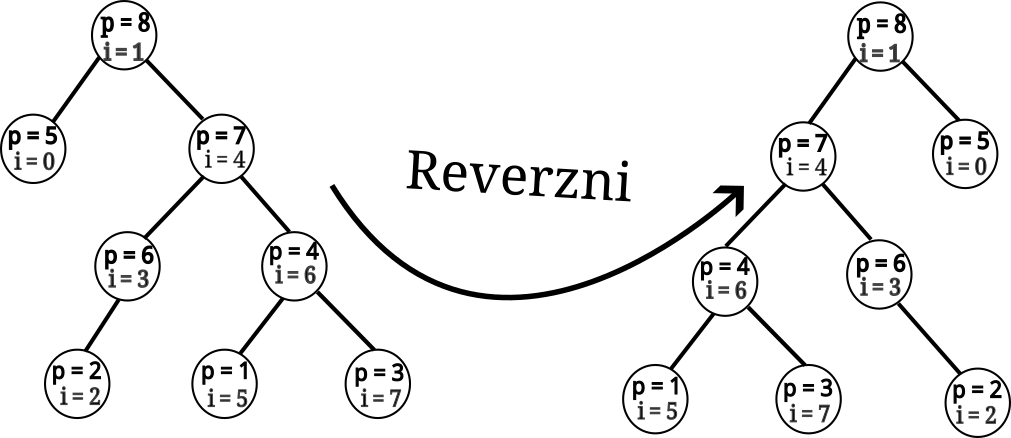
Všimnite si, že reverznutý treap je vlastne zrkadlový obraz pôvodného. Vieme ho tak dosiahnuť tak, že v každom podstrome vymeníme prvého a druhého syna, ako ilustruje nasledujúci obrázok.

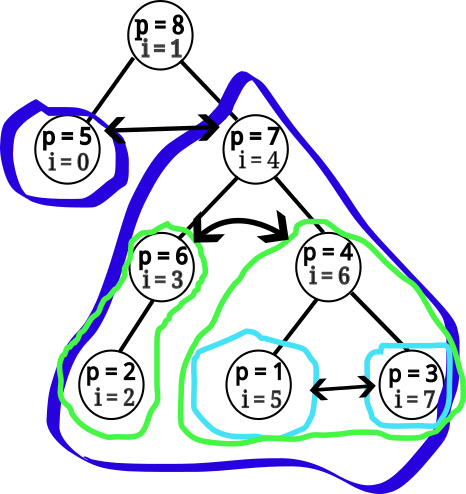
Vedeli by sme teda, rekurzívne otočiť celý strom (a vždy tiež vymeniť hodnotu miním sufixových a prefixových súčtov) v lineárnom čase od jeho veľkosti. To je však príliš pomalé.

Odpoveďou je lenivosť – nemeňme veci, kým nemusíme. Namiesto toho aby sme otáčali celý strom naraz, zaznačme si, v jeho koreni, že ho chceme otočiť. Keď sa do koreňa nabudúce pozrieme, otočíme jeho synov a vymeníme hodnoty prefixových a sufixových súčtov, a zaznačíme si do synov, že keď do nich nabudúce prídeme, majú byť otočení. Nápodobne, vždy keď dôjdeme do vrcholu v ktorom máme zaznačené, že ho treba otočiť⁴, mu vymeníme deti a príslušné hodnoty miním a deti (ak nejaké má) označíme lazy flagom, že ich treba tiež otočiť. Všimnite si, že takto vždy odpovieme správnu hodnotu (keďže nepotrebujeme otáčať celý strom, aby sme získali hodnotu pre otočený podstrom), a zároveň nám to zaberie najviac konštatne-krát viac operácií (otočíme hodnoty v jednom vrchole len vtedy keby sme s ním aj tak interagovali).⁵.

A čo s tým, keď nemáme celý treap, ale chceme iba otočiť jeho časť? Vieme použiť naše nápomocné funkcie split a merge – interval, ktorý chceme otočiť “vysekneme” z treapu pomocou splitu, označíme jeho koreň, že ho bude treba otočiť, a pomocou merge zlepíme strom nanovo, ako je zobrazené na nasledujúcom pseudokóde na otočenie intervalu medzi \(z\) a \(k\) (vrátane).

T1, T2 = split(T, z)
T2, T3 = split(T2, k - z + 1)
T2 -> otočiť = true
T = merge(T1, merge(T2, T3))

Pozor si treba dávať na to, že do funkcií split a merge treba implementovať, aby otočili podstrom(y) do ktorého/ých sa funkcia pozerá, ak sú označné na otočenie.

Takto dostaneme vzorové riešenie v rovnakom čase aj pamäti ako aj riešenie bez reverzu.

Záverečná otázka na zamyslenie: vedeli by sme funkciu reverzni implementovať v intervalovom strome?

#include<bits/stdc++.h>

using namespace std;

#define FOR(i,n)	for(int i=0;i<(int)n;i++)
#define FOB(i,n)	for(int i=n;i>=1;i--)
#define MP(x,y)	make_pair((x),(y))
#define ii pair<int, int>
#define lli long long int
#define ld long double
#define ulli unsigned long long int
#define lili pair<lli, lli>
#ifdef EBUG
#define DBG	if(1)
#else
#define DBG	if(0)
#endif
#define SIZE(x) int(x.size())
const int infinity = 2000000999 / 2;
const long long int inff = 4000000000000000999;

typedef complex<long double> point;

template<class T>
T get() {
    T a;
    cin >> a;
    return a;
}

template <class T, class U>
ostream& operator<<(ostream& out, const pair<T, U> &par) {
    out << "[" << par.first << ";" << par.second << "]";
    return out;
}

template <class T>
ostream& operator<<(ostream& out, const set<T> &cont) {
    out << "{";
    for (const auto &x:cont) out << x << ", ";
    out << "}";
    return out;
}

template <class T, class U>
ostream& operator<<(ostream& out, const map<T,U> &cont) {
    out << "{";
    for (const auto &x:cont) out << x << ", ";

    out << "}"; return out;
}

template <class T>
ostream& operator<<(ostream& out, const vector<T>& v) {
    FOR(i, v.size()){
      if(i) out << " ";
      out << v[i];
    }
    out << endl;
    return out;
}

bool ccw(point p, point a, point b) {
    if((conj(a - p) * (b - p)).imag() <= 0) return false;
    else return true;
}

struct node {
    int value, key;
    int mini, minsuf, sum, size;
    bool lazy;
    node *prvy, *druhy;

    node (int vl, int ke, node *p, node *s, bool flag): value(vl), key(ke), lazy(flag), prvy(p), druhy(s) {
        sum = (prvy == NULL ? 0 : prvy -> sum) + (druhy == NULL ? 0 : druhy -> sum) + value;
        if (prvy == NULL) {
            mini = min(0, value);
            if (druhy != NULL) {
                mini = min(mini, value + get_min(druhy));
            }
        }
        else {
            mini = min(0, min(get_min(prvy), prvy -> sum + value));
            if (druhy != NULL) {
                mini = min(mini, prvy -> sum + value + get_min(druhy));
            }
        }

        if (druhy == NULL) {
            minsuf = min(0, value);
            if (prvy != NULL) minsuf = min(minsuf, value + get_sufmin(prvy));
        }
        else {
            minsuf = min(get_sufmin(druhy), druhy -> sum + value);
            if (prvy != NULL) minsuf = min(minsuf, druhy -> sum + value + get_sufmin(prvy));
            minsuf = min(0, minsuf);
        }
        size = 1 + (prvy == NULL ? 0 : prvy -> size) + (druhy == NULL ? 0 : druhy -> size);
    }

    node *reverse() {
        return new node(value, key, prvy, druhy, !lazy);
    }

    node *propagate_lazy() {
        if (!lazy) return this;
        return new node(value, key, (druhy != NULL ? druhy -> reverse() : druhy), (prvy != NULL ? prvy -> reverse() : prvy), 0);
    }

    void print(int id, string k = "") {
        cout << k << "Node #" << id + (prvy == NULL ? 0 : prvy -> size) << ": [" << value << ", " << key << "] lazy? " << lazy << " size = " << size << " (min, sufmin) = (" << mini << ", " << minsuf  << ") sum = " << sum << endl;
        if (prvy != NULL) {
            cout << k << "First {" << endl;
            prvy -> print(id, k + "\t");
            cout << k << "}" << endl;
        }
        if (druhy != NULL) {
            cout << k << "Second {" << endl;
            druhy -> print(id + (prvy == NULL ? 0 : prvy -> size) + 1, k + "\t");
            cout << k << "}" << endl;
        }
    }

    int get_min(node *T) {
        if (T == NULL) return 0;
        return (T -> lazy ? T -> minsuf : T -> mini);
    }

    int get_sufmin(node *T) {
        if (T == NULL) return 0;
        return (T -> lazy ? T -> mini : T -> minsuf);
    }
};

node *merge (node *S, node *T) {
    if (S == NULL) return T;
    if (T == NULL) return S;

    S = S -> propagate_lazy();
    T = T -> propagate_lazy();

    if (S -> key > T -> key) {
        node *newsec = merge(S -> druhy, T);
        return new node(S -> value, S -> key, S -> prvy, newsec, S -> lazy);
    }
    node *newfir = merge(S, T -> prvy);
    return new node(T -> value, T -> key, newfir, T -> druhy, T -> lazy);
}

pair<node *, node *>split(node *T, int pos) {
    if (T == NULL) return {NULL, NULL};
    if (pos == 0) return {NULL, T};
    if (T -> size < pos) return {T, NULL};
    T = T -> propagate_lazy();

    if ((T -> prvy ==  NULL ? 0 : T -> prvy -> size) >= pos) {
        auto res = split(T -> prvy, pos);
        return {res.first, new node(T -> value, T -> key, res.second, T -> druhy, T -> lazy)};
    }

    auto res = split(T -> druhy, pos - (T -> prvy ==  NULL ? 0 : T -> prvy -> size) - 1);
    return {new node(T -> value, T -> key, T -> prvy, res.first, T -> lazy), res.second};
}

ii solve_interval(node *T, int z, int k, int sumpred) { // returns {minval, sum}
    if (T == NULL) return {sumpred, sumpred};
    T = T -> propagate_lazy();

    DBG cout << "In " << T -> key << " interval [" << z << ", " << k << ") sumpred = " << sumpred << endl;
    if (z >= k) return {sumpred, sumpred};
    if (z >= T -> size || k <= 0) return {sumpred, sumpred};

    if (z <= 0 && T -> size <= k) return {sumpred + T -> get_min(T), sumpred + T -> sum};

    auto from_first = solve_interval(T -> prvy, z, k, sumpred);
    DBG cout << "[In " << T -> key << "] From first son returns " << from_first << endl;

    if (T -> prvy != NULL && k <= T -> prvy -> size) return from_first;
    if ((T -> prvy != NULL ? T -> prvy -> size : 0) < z) return solve_interval(T -> druhy, z - 1 - (T -> prvy == NULL ? 0 : T -> prvy -> size), k - 1 - (T -> prvy == NULL ? 0 : T -> prvy -> size), sumpred);

    int minsofar = min(from_first.first, from_first.second + T -> value);
    int sumsofar = from_first.second + T -> value;

    auto from_second = solve_interval(T -> druhy, z - 1 - (T -> prvy == NULL ? 0 : T -> prvy -> size), k - 1 - (T -> prvy == NULL ? 0 : T -> prvy -> size), sumsofar);
    DBG cout << "[In " << T -> key << "] From second vracia " << from_second << endl;
    return {min(minsofar, from_second.first), from_second.second};
}

node *swap_val(node *T, int p, int nv) {
    if (T == NULL) return T;
    T = T -> propagate_lazy();
    if (p < (T -> prvy == NULL ? 0 : T -> prvy -> size)) return new node(T -> value, T -> key, swap_val(T -> prvy, p, nv), T -> druhy, T -> lazy);
    if (p == (T -> prvy == NULL ? 0 : T -> prvy -> size)) return new node(nv, T -> key, T -> prvy, T -> druhy, T -> lazy);
    return new node(T -> value, T -> key, T -> prvy, swap_val(T -> druhy, p - 1 - (T -> prvy == NULL ? 0 : T -> prvy -> size), nv), T -> lazy);
}

node* insert_node(node *T, int p, int nv, int key) {
    if (T == NULL) return new node(nv, key, NULL, NULL, 0);
    T = T -> propagate_lazy();
    if (key > T -> key) {
        auto prel = split(T, p);
        return new node(nv, key, prel.first, prel.second, 0);
    }
    if (p <= (T -> prvy == NULL ? 0 : T -> prvy -> size)) {
        return new node(T -> value, T -> key, insert_node(T -> prvy, p, nv, key), T -> druhy, T -> lazy);
    }
    return new node(T -> value, T -> key, T -> prvy, insert_node(T -> druhy, p - (T -> prvy == NULL ? 0 : T -> prvy -> size) - 1, nv, key), T -> lazy);
}

node *erase_interval(node *T, int a, int b) {
    auto split1 = split(T, a);
    auto split2 = split(split1.second, b - a);
    return merge(split1.first, split2.second);
}

node *reverse_interval(node *T, int a, int b) {
    auto split1 = split(T, a);
    auto split2 = split(split1.second, b - a);
    return merge(split1 .first, merge((split2.first != NULL ? split2.first -> reverse() : NULL), split2.second));
}

int main() {
    cin.sync_with_stdio(false);
    cout.sync_with_stdio(false);

    int n = get<int>();
    int q = get<int>();

    string r = get<string>();
    node *root = NULL;
    FOR(i, n) {
        root = insert_node(root, i, (r[i] == 'V' ? 1 : -1), rand());
        DBG root -> print(0);
    }

    DBG cout << "Queries: " << endl;

    FOR(i, q) {
        string query = get<string>();
        if (query == "vysledok") {
            int a = get<int>();
            int b = get<int>() + 1;
            ii res = solve_interval(root, a, b, 0);
            DBG cout << "res = " << res << endl;
            cout << (- res.first) + (res.second - res.first) + (b - a) << endl;
        }
        else if (query == "vymen") {
            int a = get<int>();
            int b = (get<char>() == 'V' ? 1 : -1);
            root = swap_val(root, a, b);
        }
        else if (query == "pridaj") {
            int a = get<int>();
            int b = (get<char>() == 'V' ? 1 : -1);
            root = insert_node(root, a, b, rand());
        }
        else if (query == "zmaz") {
            int a = get<int>();
            int b = get<int>() + 1;
            root = erase_interval(root, a, b);
        }
        else if (query == "reverzni") {
            int a = get<int>();
            int b = get<int>() + 1;
            root = reverse_interval(root, a, b);
        }
        DBG if (root != NULL) root -> print(0);
        DBG cout << "End of query " << i << ": " << query << endl;
    }
}