Zadanie
Kristína si ráno čítala maily a našla tam pozvánku na nejaký výlet od Marcela. Nakoľko len pred chvíľou vstala, bez menšieho zaváhania otvorila prihlášku a začala vypĺňať. Keď už bola na konci, narazila na najťažšiu otázku: “Ako dlhá by mala byť trasa výletu?”. Kike sa z rána veľmi nechcelo rozmýšľať, tak rovno napísala “Ja nevieeem”.
Keď si Marcel pozeral prihlášky a zbadal túto odpoveď, hneď mu bolo jasné, čo musí spraviť. Musí pripraviť vhodnú trasu na každú dĺžku. Ak by nejaká dĺžka chýbala, Kika by si vybrala presne tú a celý deň by sa sťažovala (čo ale teda neznamená, že to nebude robiť aj tak).
Marcel teda naplánoval perfektné trasy všetkých dĺžok. Začiatok majú všetky spoločný, no koncov je už niekoľko. Nakreslil si aj mapku, vyznačil začiatok, cieľové body, rázcestia a teraz mu ostáva už len označiť odbočky pri rázcestníkoch. Nebude to však také ľahké. Marcel by chcel, aby všetky trasy mohol popísať jedným slovom, nech si to Kika zapamätá!
Presnejšie musí platiť nasledovné:
- Slovo popisujúce trasy má rovnakú dĺžku ako najdlhšia trasa.
- Trasu dĺžky \(k\) nájdeme nasledovaním posledných \(k\) písmen slova.
- Z každého rázcestia vychádza niekoľko ciest označených rôznymi písmenami.
- V každom cieľovom bode končí aspoň jedna trasa.
- Každá trasa končí v nejakom ceľovom bode.
Napríklad, ak je slovo abbab, tak trasy, ktoré končia v
cieli nájdeme, iba ak budeme nasledovať slová abbab,
bbab, bab, ab, b
alebo ostaneme v začiatočnom vrchole (pre prípad, že by sa Kike vôbec
nechcelo chodiť).
Úloha
Na vstupe dostanete orientovaný graf a zoznam cieľových vrcholov.
Vašou úlohou je doplniť ku hranám písmená tak, aby graf spĺňal Marcelove podmienky pre nejaké slovo \(w\) a nájsť nejaké takéto slovo.
Pre jednoduchosť budeme namiesto písmen používať celé čísla od \(1\) do \(k\), pričom jediná podmienka je, že \(k \le m\). Môžete tiež predpokladať, že graf, ktorý dostanete sa dá označiť tak, aby Marcelove podmienky spĺňal.
Formát vstupu
Na prvom riadku dostanete tri celé čísla - počet vrcholov \(n\), počet orientovaných hrán \(m\) a počet cieľových vrcholov \(t\) (\(1 \le t \le n\)).
V druhom riadku dostanete \(t\) celých čísel – cieľové vrcholy.
Nakoniec nasleduje \(m\) riadkov, popisujúcich hrany v grafe. Na každom riadku sú dve medzerou oddelené čísla \(s_i\) a \(t_i\), označujúce hranu z vrcholu \(s_i\) do vrcholu \(t_i\). Vrcholy sú označené číslami od \(1\) do \(n\), pričom vrchol \(1\) je vždy začiatočný.
Úloha má 4 sady, pre ktoré platia nasledujúce obmedzenia:
| Sada | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(1 \leq n \leq\) | \(60\) | \(6 \cdot 10^3\) | \(2 \cdot 10^5\) | \(3 \cdot 10^5\) |
| \(1 \leq m \leq\) | \(60\) | \(6 \cdot 10^3\) | \(2 \cdot 10^5\) | \(3 \cdot 10^5\) |
| \(1 \leq t \leq\) | \(60\) | \(3 \cdot 10^2\) | \(5 \cdot 10^2\) | \(8 \cdot 10^2\) |
Formát výstupu
Na prvý riadok výstupu vypíšte dve čísla \(l\) a \(k\) - dĺžka slova \(w\) a počet rôznych čísel na hranách. Na druhý riadok vypíšte slovo \(w\) ako \(l\) celých čísel medzi \(1\) a \(k\) oddelených medzerami.
Na tretí riadok vypíšte \(m\) čísel – označenia hrán v poradí, v akom sú na vstupe tak, aby graf spĺňal Marcelove podmienky.
Príklad
Input:
7 8 4
1 3 4 7
1 2
1 3
2 4
3 5
3 6
4 5
5 6
6 7Output:
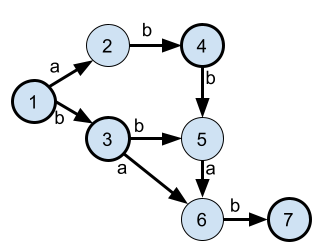
5 2
1 2 2 1 2
1 2 2 2 1 2 1 2Riešenie je zobrazené na obrázku kde \(1\) predstavuje a a \(2\) b
Zadanie tejto úlohy hovorí, že máme pre orientovaný graf nájsť nejaké ohodnotenie hrán, tak aby spĺňalo niekoľko podmienok. Tento orientovaný graf má navyše vyznačený štartovací vrchol a niekoľko cieľových vrcholov. Nemenej dôležitá je informácia, že v cieľových vrcholoch končia cesty ktoré popisujú sufixy nejakého slova (alebo postupnosti čísel v našom prípade).
Keďže sú to sufixy, môžeme si všinúť, že každá trasa končí rovnakým číslom, teda napríklad \(1\). Z toho nám hneď vyplýva, že hrany ktoré vedú do cieľových vrcholov musia niesť práve číslo \(1\). Získali sme jeden znak riešenia. Aby sme mohli určiť nasledujúci, stačí sa posunúť po hranách ktoré sme prave označili. My totiž vieme, že všetky cesty sú sufixy, takže aj predposledné písmeno musia mať rovnaké. Pozrieme sa teda na všetky hrany ktoré vedú ku tým ktoré sme práve označili a vieme že musia mať rovnaké číslo. Ak o niektorej hrane vieme, aké má číslo, tak ho len priradíme všetkým ostatným a máme druhý znak riešenia. Ak žiadna z hrán ešte číslo nemá, musíme im priradiť nejaké nové číslo (napríklad \(2\)).
Tento postup následne stačí opakovať, až kým sa dostaneme do takého stavu, že do daných vrcholov žiadne hrany nevedú. Vtedy sme sa totiž všetkými cestami dostali do štartovného vrcholu a ak si medzičasom budeme aj zapisovať čísla ktoré hranám priraďujeme, máme aj finálne slovo, skonštruované od konca.
Implementácia
Postup popísaný vyššie je v podstate BFS, teda prehladávanie do šírky1. Zásadný rozdiel je v tom, že graf neprehľadávame z jedného počiatočného vrchola, ale zo všetkých cieľových vrcholov ako počiatočných naraz a posúvame sa po hranách v opačnom smere. Aby sa to viac podobalo na BFS, môžeme si predstaviť že máme ešte jeden cieľ, z ktorého vedie hrana práve do tých vrcholov, ktoré sú cieľové. Potom sa to už podobá na klasické BFS z tohoto vrchola.
Druhý rozdiel od klasickej implementácie BFS je v tom, že sa potrebujeme vždy pozerať na celú “vrstvu” vrcholov, ktoré sú v rovnakej vzdialenosti od cieľa. Toto dosiahneme jednoducho tak, že namiesto toho aby sme z fronty vyberali jeden vrchol, vyberieme ich naraz všetky. To budú totiž vrcholy v rovnakej vzdialenosti. Následne ich spracujeme, teda pozrieme sa na všetky hrany ktoré do nich vedú, nájdeme medzi nimi ohodnotenú, alebo vyberieme nové číslo a všetky tieto hrany ohodnotíme. Až po tomto kroku pridáme do fronty nové vrcholy, teda začiatky novoohodnotených hrán, ktoré sú opäť o jedna ďalej od cieľa. Inak povedané, vo fronte bude jedno pole vrcholov ktoré sú v rovnakej vzdialenosti od cieľa, a teda to vlastne ani nemusí byť fronta.
Časová a pamäťová zložitosť
Čo si treba uvedomiť je, že síce hovoríme že je to “nejaké BFS”, ale v skutočnosti to nie je jedno prehľadanie grafu. Aby sme mohli povedať že je to lineárne, mselo by platiť že každú hranu prejdeme konštantný počet krát – čo nie je pravda.
Náš algoritmus dá na začiatku do fronty všetky cieľové vrcholy, tých môže byť najviac \(n\). V ďalšom kroku pridávame do fronty všetky vrcholy pred nimi. Tých môže byť najviac \(n-1\), pretože jedna z ciest patrila suffixu dĺžky 1 a tou sme sa už dostali do cieľa. Rovnako v každom ďalšom kroku nám určite jedna cesta vypadne a teda v najhoršom prípade budeme do fronty pridávať postupne \(n, n-1, n-2, \cdots, 1\) vrcholov čo je spolu \(O(n^2)\). Čo sa pamäte týka, ukladáme si vstup, a niekoľko pomocných štruktúr, koré nepresahujú veľkosť vstupu, teda pamäťová zložitosť je \(O(m+n)\)
n, m, t = [int(x) for x in input().split()]
terminal = [int(x)-1 for x in input().split()]
hrany = [] # zoznm hran
susedia = [[] for x in range(n)] # zoznam susedov
for i in range((m)):
a, b = [int(x)-1 for x in input().split()]
susedia[b].append(a) # ukladame opacne hrany
hrany.append((a,b))
oznacenia = {}
fronta = set(terminal)
dalsie_cislo = 1
slovo = []
while len(fronta)!=0:
oznacenie = dalsie_cislo
nova_fronta = set()
for v in fronta:
for s in susedia[v]:
nova_fronta.add(s)
if oznacenia.get((v,s)) != None:
oznacenie = oznacenia.get((v,s))
for v in fronta:
for s in susedia[v]:
oznacenia[(v,s)] = oznacenie
fronta = nova_fronta
if oznacenie == dalsie_cislo:
dalsie_cislo += 1
slovo.append(oznacenie)
slovo.pop()
slovo.reverse()
print(len(slovo), dalsie_cislo-2)
print(*slovo)
print(*[oznacenia[(b,a)] for (a,b) in hrany])Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.