Zadanie
Keďže je Kristína nadšená cestovateľka, ako už bolo niekde spomenuté, po nejakom čase sa rozhodla ísť na dlhú dovolenku do provincie Småland na juhu Švédska. Ak ste nevedeli, Småland obsahuje jeden z najväčších systémov súostroví na svete, a tým, že sa Kika celkom nudila, rozhodla sa, že prejde všetky ostrovy v ňom.
Kika nevie plávať (a na jar v Baltskom mori ani veľmi nechce), ale, naštastie, vo vyspelých severských krajinách to chodí tak, že každú chvíľu sa medzi nejakými dvomi ostrovmi postaví most, po ktorom vie prejsť. Samozrejme, nie vždy sú všetky ostrovy poprepájané, a tak súostrovie obsahuje len skupinky prepojených ostrovov.
V takto vytvorených skupinkách väčšinou bývajú takzvané špeciálne ostrovy ™, ktoré sú napojené len jedným mostom so zvyškom skupinky, a teda pokiaľ Kika na takýto ostrov príde, jej jediná možnosť je vrátiť sa po tom istom moste naspäť.
Kristína by pre potreby plánovania výletu rada vedela, koľko takých špeciálnych ostrovov vie z nejakého ostrovu navštíviť len prechádzaním po mostoch. Môže sa pohybovať ako chce a ostrovmi aj mostami môže prechádzať koľkokrát chce v ľubovoľnom smere (je predsa na dovolenke, nie na diaľnici).
Úloha
Vašou úlohou bude zisťovať, koľko špeciálnych ostrovov vie Kika dosiahnuť z ľubovoľného ostrova v závislosti od toho, aké mosty sú v danom čase postavené. Budete začínať len s izolovanými ostrovmi. Kedykoľvek môžete dostať informáciu, že sa postavil most medzi nejakými ostrovmi \(a\) a \(b\). Taktiež sa Vás kedykoľvek môže Kika spýtať, na koľko špeciálnych ostrovov sa vie z nejakého ostrovu \(x\) dostať. Informácie o mostoch a otázky o špeciálnych ostrovoch budeme súhrnne označovať queries.
Formát vstupu
V prvom riadku vstupu sú dve čísla \(n\) a \(q\). Číslo \(n\) udáva, koľko je ostrovov v súostroví, číslo \(q\) zase koľko dostanete queries.
Nasledovať bude \(q\)
jednoriadkových queries, ktoré budú mať buď tvar
! a b (bol postavený most medzi ostrovmi \(a\) a \(b\)) alebo ? x (Kika sa pýta,
na koľko špeciálnych ostrovov sa vie dostať z ostrovu \(x\)).
Sú 4 sady vstupov, môžete v nich predpokladať nasledujúce obmedzenia:
| Sada | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(1 \leq n \leq\) | \(100\) | \(10^4\) | \(10^5\) | \(10^6\) |
| \(1 \leq q \leq\) | \(200\) | \(2 \cdot 10^4\) | \(2 \cdot 10^5\) | \(2 \cdot 10^5\) |
Formát výstupu
Na informáciu o stavbe mosta nevypisujete nič. Na otázku o špeciálnych ostrovoch vypíšte počet takýchto ostrovov.
Príklady
Input:
3 4
! 0 2
? 0
? 2
? 1Output:
2
2
0Vytvorili sme most medzi ostrovmi 0 a
2. Z ostrova 0 sa vieme dostať na 2 špeciálne
ostrovy (vrátane toho, na ktorom stojíme). Z ostrova 1 sa
nevieme dostať na žiadny špeciálny ostrov, pretože je
izolovaný.
Input:
6 8
! 0 2
! 2 4
! 1 3
! 1 5
? 0
? 5
! 0 1
? 3Output:
2
2
3Pred prvými otázkami nám vzniknú dve skupinky ostrovov, každá má
2 špeciálne ostrovy. Potom spojíme špeciálny ostrov 0 z
prvej skupinky s normálnym ostrovom 1 z druhej skupinky,
čím nám vznikne veľká skupina ostrovov s 3 špeciálnymi
ostrovmi.
Táto úloha bola grafový problém. Ak ste o grafoch1 ešte nepočuli, v Kuchárke KSP je k nim pekný úvod.
V našej úlohe sú teda ostrovy vrcholmi grafu a mosty medzi nimi hranami grafu. Potom skupinky ostrovov budú komponenty súvislostí a špeciálne ostrovy sú vrcholy stupňa 1, ktoré tiež niekedy nazývame listy grafu.
Len pre doplnenie, graf si môžete predstaviť ako “sieť”, kde vrcholy sú body spájané čiarami, čo sú hrany. Komponent súvislostí je potom taká skupinka vrcholov, v ktorej vieme po hranách prejsť z každého vrcholu do každého. Nakoniec, stupeň vrchola je počet hrán, ktoré sa na neho napájajú (odborne povieme, že tieto hrany sú s ním incidentné).
V úlohe sme začínali s \(n\) izolovanými vrcholmi, pričom každý z nich je samostatný komponent súvislostí s jedným vrcholom.
Ak sme niekedy dostali query na stavbu mostu ! a b, vytvorili sme v podstate hranu medzi nejakými vrcholmi \(a\) a \(b\), čím sme spojili ich dva komponenty súvislostí do jedného spoločného.
Ak sme dostali otázku typu ? x, pýtali sme sa vlastne na počet listov v komponente, ktorý obsahuje vrchol \(x\).
Jednoduché riešenie
Najjednoduchší spôsob, ako sa dala táto úloha riešiť bolo simulovať graf presne tak, ako vzniká. To znamená, že sme si pamätali všetky hrany grafu, a keď nám prišla query na vytvorenie hrany, tak sme ju pridali do grafu. Keď nám prišla otázka na počet listov, tak sme spustili z tohoto vrcholu nejaké prehľadávanie, napríklad DFS, ktorým sme zistili počet listov.
Pridávanie hrany do grafu vieme robiť v zložitosti \(O(1)\). Keď zisťujeme počet listov, tak musíme v najhoršom prípade prehľadať celý graf, čo vieme urobiť v zložitosti \(O(n+m)\) (kde \(n\) je počet vrcholov a \(m\) počet hrán). Pamäťová zložitosť je \(O(n+m)\), keďže si potrebujeme pamätať celý graf.
Pomalšie riešenie
Iný spôsob, ako túto úlohu riešiť, ktorý je aj základ pre vzorové riešenie je tak, že sme rovno simulovali komponenty.
Komponenty sme si uchovávali v nejakom poli. Každý komponent si pamätá, aké vrcholy obsahuje a koľko z týchto vrchol je listov. Tiež si niekde uchovávame informáciu o tom, aký stupeň má každý vrchol.
Ak potom dostaneme inštrukciu na stavbu mostu medzi vrcholmi \(a\) a \(b\), stačí nám vyhľadať, v ktorých komponentoch sa tieto vrcholy nachádzajú.
Ak sú v rovnakom komponente, nič sa nedeje, len im upravíme stupeň, pretože sme medzi nimi vytvorili hranu. Tiež, ak bol nejaký z nich list, tak už nie je, a teda komponentu upravíme informáciu o tomto.
Ak sú ale komponenty obsahujúce dané vrcholy odlišné, musíme ich zlúčiť, čiže chceme záznamy o vrcholoch z jedného komponentu premiestniť do druhého. Ostatné informácie o stupňoch vrcholov a listoch upravíme rovnako, ako v predchádzajúcom prípade.
Ak sa niekedy spýtame na počet listov v komponente nejakého vrcholu, stačí nám jednoducho vyhľadať, v ktorom komponente je daný vrchol a pozrieť sa do záznamov, koľko listov má daný komponent.
Ako ste si mohli všimnúť, najpomalšia operácia, ktorú tu vykonávame, je vyhľadávanie vrcholu v komponente. V tomto prípade však časová zložitosť tejto operácie záleží od konkrétnej implementácie a voľby dátovej štruktúry reprezentujúcej komponenty alebo vrcholy.
Vyššie navrhnuté riešenie s použitím polí pre komponenty by malo časovú zložitosť vyhľadávania vrcholu \(O(n)\).
Keďže si uchovávame v poli zoznam komponentov a pre každý komponent zoznam ich vrcholov, pamäťová zložitosť bude \(O(n)\), pretože pokiaľ premiestňujeme vrcholy medzi poľami, uchovávať budeme stále \(n\) vrcholov.
Za takéto a podobne rýchle riešenia ste mohli získať 2 body.
V prípade, že ste robili to, že ste vždy spájali menší komponent do väčšieho, dá sa ukázať, že takéto spájanie komponentov má amortizovanú časovú zložitosť \(O(\log n)\).
Niečo trochu lepšie
V predchádzajúcom riešení sme mali problém s pomalým prehľadávaním a spájaním komponentov.
O komponentoch súvislostí však vieme, že sú navzájom disjunktné2, a že spojenie dvoch komponentov urobíme prepojením dvoch vrcholov, ktoré sú v nich obsiahnuté.
Toto vieme využiť na to, že komponenty už nebudeme reprezentovať ako polia vrcholov, ale ako stromy. Opäť, ak ste sa ešte so stromami nestretli, krátky úvod nájdete znova v Kuchárke KSP.
Na začiatku máme izolované vrcholy, čiže jednovrcholové komponenty súvislostí zodpovedajúce stromom s jedným vrcholom:

Ak spojíme vrcholy 1 a 2 (vykonáme ! 1 2), spojíme aj ich stromy, čiže len jeden zavesíme na druhý:

Spravme to isté pre vrcholy 3 a 4:
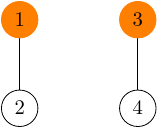
Teraz ak chceme spojiť napríklad vrcholy 2 a 4 do jedného komponentu, mohli by sme ich na seba zavesiť ako chceme, ale najlepšie to bude urobiť takto:
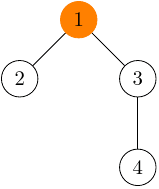
Ako asi vidíte, dva vrcholy sú v rovnakom komponente, ak majú spoločný koreň^ [Najvyšší vrchol v strome, nemá rodičovský vrchol] (označený oranžovo na obrázkoch vyššie). Tiež ak chceme zistiť, v akom komponente sa vrchol nachádza, nepotrebujeme už prehľadávať všetky komponenty, stačí nám len sledovať, akého rodiča má daný vrchol a sledovať jeho rodiča rodiča a tak ďalej, až kým neprídeme ku koreňu, ktorý reprezentuje náš komponent.
Pre každý vrchol nám potom stačí uchovávať si len jeho rodiča, pričom korene, teda vrcholy, ktoré nemajú rodičov, budú rodičmi samým sebe.
Ak teraz budeme chcieť spojiť nejaké dva komponenty hranou medzi vrcholmi \(a\) a \(b\) (! a b), jednoducho budeme sledovať rodičov každého vrcholu, až kým sa nedopracujeme ku koreňu (volajme ho reprezentant).
Ak je reprezentant rovnaký, oba vrcholy sú v rovnakom komponente. Ak sú reprezentanti odlišní (nazvime si ich \(r_a\) a \(r_b\)), môžeme napríklad koreňu \(r_a\) priradiť ako rodiča \(r_b\), čiže nový veľký komponent bude mať \(r_b\) ako reprezentanta.
Informácie o stupňoch vrcholov si uchovávame rovnako, ako v predchádzajúcom riešení. Aktuálny počet listov daného komponentu bude uložený pre daného reprezentanta.
Ak sa potom spýtame na počet listov pre komponent nejakého vrcholu, stačí nám nájsť jeho reprezentanta a pozrieť sa v nejakom poli na zodpovedajúce miesto.
To, čo sme tu objavili, sa volá Union-find alebo Disjoint-set data structure, resp. jeho naivná implementácia (v ďalšej sekcii si ukážeme, ako môže vyzerať sofistikovanejšia implementácia).
Keďže vyhľadávame v stromoch, časová zložitosť vyhľadávania bude prinajhoršom \(O(n)\), keď máme len jeden komponent a všetky vrcholy v ňom majú presne jedného potomka. Potom ten strom vyzerá viac ako stožiar, a teda musíme prejsť všetkých \(n\) vrcholov, aby sme sa dostali až k reprezentantovi.
Tu sme si teda rýchlosťou veľmi nepomohli oproti predchádzajúcemu riešeniu, avšak voľba union-find dátovej štruktúry nám dáva možnosť pridať rôzne optimalizácie, ktoré to zrýchlia.
Časová zložitosť spájania komponentov, teda stavania mostov, bude tiež \(O(n)\), pretože stále musíme hľadať reprezentantov. Časová zložitosť na query je teda lineárna.
Pamäťová zložitosť je stále \(O(n)\) rovnako, ako v predchádzajúcom riešení, pretože stále nám na toto všetko stačia len polia.
Optimálne riešenie
Dá sa to ešte lepšie? Áno, dá. Vďaka tomu, že si komponenty reprezentujeme ako union-find dátovú štruktúru, dokážeme urobiť nejaké optimalizácie.
Ak sa zamyslíte, zistíte, že komponenty s veľkým počtom vrcholov budú eventuálne reprezentované dosť hlbokými stromami. Napríklad, takto by mohol vyzerať strom reprezentujúci 7-vrcholový komponent:
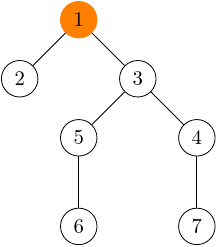
Ak by sme teraz chceli nájsť reprezentanta tohto komponentu z vrcholu 7, trvalo by nám trochu dlhšie dopracovať sa až do oranžového koreňa. Viete si potom asi predstaviť, aké neefektívne by bolo prechádzať hlboký strom pre komponenty s niekoľkými tisícmi vrcholov.
Tento problém ale vieme jednoducho vyriešiť. Ak napríklad budeme prechádzať strom od vrcholu 7, zároveň s hľadaním reprezentanta môžeme tiež prelinkovať prechádzaný vrchol na prarodiča3 nášho vrcholu. V našom prípade by to mohlo vyzerať takto:
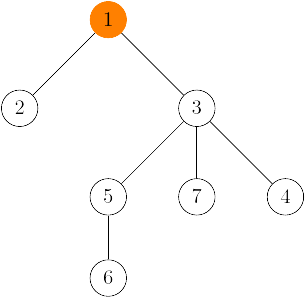
Odteraz ak niekedy budeme znovu potrebovať prechádzať strom od vrcholu 7, ušetríme si jeden krok a nič sme nepokazili, pretože nás zaujíma len príslušnosť vrcholu k reprezentantu, nie štruktúra stromu.
Tento proces sa nazýva lazy path halving. Lazy preto, lebo toto robíme len keď máme potrebu prechádzať strom z nejakého vrcholu. Path halving odkazuje zas na to, že vrcholy prelinkovávame na prarodičov, čiže “preskočíme” polovicu úrovní na ceste ku koreňu, a teda dĺžka cesty sa skráti na polovicu.
Vo všeobecnosti tento mechanizmus ale nazývame path compression a path halving je len jeho konzervatívnejšia forma. V podobnom duchu ale môžeme robiť aj extrémnejšie úpravy stromu:
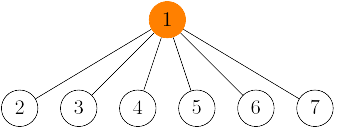
Ďalší problém, ktorý nám v praxi môže spomaliť naše riešenie je ten, že pri naivnej implementácii spájame komponenty len tak, že ku koreňu stromu jedného komponentu pripojíme koreň stromu druhého komponentu.
Potom vymyslime si takéto dva stromy reprezentujúce komponenty:
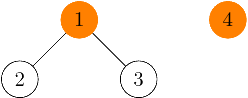
Ich zjednotenie naivnou implementáciou union-findu z predchádzajúceho riešenia bude vyzerať takto:
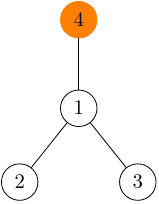
Tento nový strom má hĺbku 2, čiže na nájdenie reprezentanta by sme potrebovali spraviť dva kroky hore stromom. Pritom kľudne by sme vedeli postaviť aj efektívnejší strom s hĺbkou len 1:
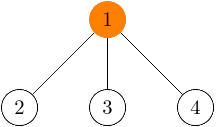
Čo sa stalo? V naivnej implementácii napájame stromy na seba nemenne len jedným spôsobom a neberieme ohľad na to, ako bude vyzerať výsledok. V praxi potom naše stromy budú veľakrát vyzerať ako palice s veľkou hĺbkou, čiže opäť naša najdôležitejšia úloha hľadania reprezentanta bude prebiehať pomalšie.
Ideálne by sme ale chceli mať viac “rozkošatené” stromy s čo najviac vrcholmi na jednej úrovni, aby sme mali plytké stromy, v ktorých sa vieme rýchlo dostať do koreňa.
Jedna z možností, ako takúto vlastnosť zabezpečiť, je pripájať koreň menšieho stromu (s menším počtom vrcholov) ku koreňu väčšieho stromu. To vieme jednoducho implementovať napríklad tak, že si pre každý koreň uložíme, koľko má jeho strom vrcholov. Keď potom spájame dva stromy, len si porovnáme ich veľkosti a podľa toho sa rozhodneme, ako ich chceme spojiť.
Tejto technike sa hovorí weighted union alebo konkrétnejšie union by size.
Najhoršia časová zložitosť hľadania reprezentanta s weighted union bez path compression bude \(O(\log n)\), pretože budeme hľadať vo vyváženom strome, v ktorom budeme musieť spraviť najviac toľko krokov hore, aká je jeho hĺbka.
Toto sa ale zmení, keď pridáme path compression. Kombinácia týchto dvoch mechanizmov potom bude mať amortizovanú časovú zložitosť \(O\left(\log^* n\right)\), kde \(\log^*\) je iterovaný logaritmus, ktorý vráti počet logaritmovaní, ktoré musíme aplikovať na pôvodnú hodnotu, kým nedostaneme výsledok menší alebo rovný 1. Môžete si to predstaviť tak, že nám vráti počet, koľkokrát musíme na kalkulačke stlačiť tlačidlo logaritmu, aby sme dostali výsledok menší alebo rovný 1.
Časová zložitosť tejto verzie union-findu sa zvykne ešte označovať aj ako \(O\left(\alpha(n)\right)\), kde \(\alpha(n)\) je takzvaná inverzná Ackermannova funkcia, ktorá rastie podobne extrémne pomaly ako \(\log^* n\). Keďže \(\alpha(n) \leq 5\) pre \(n < 2^{65536}\)4, tak prakticky pre akékoľvek vstupy dostávame konštantnú časovú zložitosť \(O(1)\) na query.
Presná analýza časovej zložitosti sa v tomto prípade dosť komplikovane odvádza, ale pokiaľ by Vás to zaujímalo, môžete sa pozrieť napríklad sem.
Pamäťová zložitosť bude opäť rovnaká, ako v predchádzajúcich riešeniach, teda \(O(n)\) pretože si stále vystačíme s niekoľkými lineárnymi poľami.
Za takéto a podobné riešenia využívajúce dostatočne rýchlu implementáciu union-findu ste mohli získať plný počet bodov.
"""
Union-find solution with path halving and weighted union
Should have O(alpha(n)) - near-constant amortized time complexity for union and find
O(n) space complexity
"""
def find(x: int) -> int:
"""
Find the root vertex of a component the vertex `x` belongs to.
Perform path halving along it.
"""
# Traverse the union find tree
while parents[x] != x:
parents[x] = parents[parents[x]]
x = parents[x]
return x
# Number of vertices and queries
n, q = map(int, input().split())
# Union find root list and sizes component sets for weighted union
parents = list(range(n))
sizes = [1] * n
# Number of leaves in component a vertex belongs to
# and degrees of vertices just to check whether a vertex is a leaf
n_leaves = [1] * n
degrees = [0] * n
for _ in range(q):
q_type, *info = input().split()
# Create an edge
if q_type == '!':
u, v = map(int, info)
# Find parent vertices of components vertices u, v belongs to
parent_v = find(v)
parent_u = find(u)
# If u, v are not in the same component
if parent_u != parent_v:
# Merge the components by performing weighted union of sets
# Try to balance both sets' sizes controlling the tree height
if sizes[parent_u] < sizes[parent_v]:
parents[parent_u] = parent_v
sizes[parent_v] += sizes[parent_u]
# Modify number of leaves in the created component
n_leaves[parent_v] += n_leaves[parent_u] - ((degrees[u] == 1) + (degrees[v] == 1))
else:
parents[parent_v] = parent_u
sizes[parent_u] += sizes[parent_v]
n_leaves[parent_u] += n_leaves[parent_v] - ((degrees[u] == 1) + (degrees[v] == 1))
else:
# Change the number of leaves in the component if we are creating an edge between leaves
n_leaves[parent_v] -= (degrees[u] == 1) + (degrees[v] == 1)
degrees[u] += 1
degrees[v] += 1
# Get the number of leaves in a component
elif q_type == '?':
v = int(info[0])
parent = find(v)
print(
0 if degrees[v] == 0
else n_leaves[parent]
)// C++ version of sol.py
#include <iostream>
#include <vector>
#include <numeric>
int findRoot(int x, std::vector<int> &parents) {
int modX = x;
while (parents[modX] != modX) {
parents[modX] = parents[parents[modX]];
modX = parents[modX];
}
return modX;
}
int main() {
int n, q;
std::cin >> n >> q;
std::vector<int> parents(n), sizes(n, 1);
std::iota(parents.begin(), parents.end(), 0);
std::vector<int> nLeaves(n, 1), degrees(n, 0);
for (int i = 0; i < q; i++) {
char qType;
std::cin >> qType;
if (qType == '!') {
int u, v;
std::cin >> u >> v;
int parentV = findRoot(v, parents);
int parentU = findRoot(u, parents);
if (parentU != parentV) {
if (sizes[parentU] < sizes[parentV]) {
parents[parentU] = parentV;
sizes[parentV] += sizes[parentU];
nLeaves[parentV] += nLeaves[parentU] - ((degrees[u] == 1) + (degrees[v] == 1));
}
else {
parents[parentV] = parentU;
sizes[parentU] += sizes[parentV];
nLeaves[parentU] += nLeaves[parentV] - ((degrees[u] == 1) + (degrees[v] == 1));
}
}
else {
nLeaves[parentV] -= (degrees[u] == 1) + (degrees[v] == 1);
}
degrees[u] += 1;
degrees[v] += 1;
}
else if (qType == '?') {
int v;
std::cin >> v;
int parent = findRoot(v, parents);
std::cout << ((degrees[v] == 0) ? 0 : nLeaves[parent]) << std::endl;
}
}
return 0;
}Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.