7. Áááá, záplavy vzorové riešenie

3       // prvá časť vstupu
1 2
2 3
1 1     // prvá púť
1 3     // druhá púť
0       // ukončenie vstupu

1 1     // pozície hrobiek
1 2
2 2
1       // odpoveď na prvú otázku
1 1 1 1
2       // odpoveď na druhú otázku
1 1 1 2
2 2 2 2

Táto úloha má dve časti. V prvej potrebujeme položiť strom (sieť hrobiek posvätných hovniválov) do roviny (\(n \times n\) mriežky), tak aby sme následne v druhej časti vedeli pre ľubovoľný pár vrcholov vybrať dva neprekrývajúce sa obdĺžniky, ktoré pokrývajú presne vrcholy na ceste medzi nimi.

Predstavme si zakorenený strom. Vtedy si každú cestu vieme rozdeliť na dve časti, v ktorých ideme len hore:

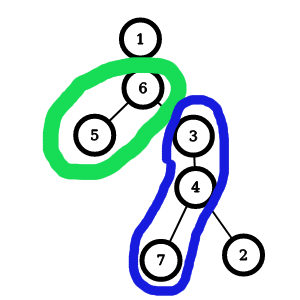
Nápad, na ktorom vzorák postavíme, je nasledovný: zakoreníme strom a posadíme ho do roviny tak, aby sme každú cestu dohora vedeli položiť do obdĺžnika.

Následne, aby sme pre pár vrcholov našli (najviac) dva neprekrývajúce sa obdĺžniky, najskôr nájdeme ich najbližšieho spoločného predka. Takto cestu rozdelíme na dve cesty dohora a tie vieme pokryť.

Položenie stromu do roviny

Binárny strom

Najskôr si zobme prípad binárneho stromu. Položme koreň stromu do ľavého horného rohu.

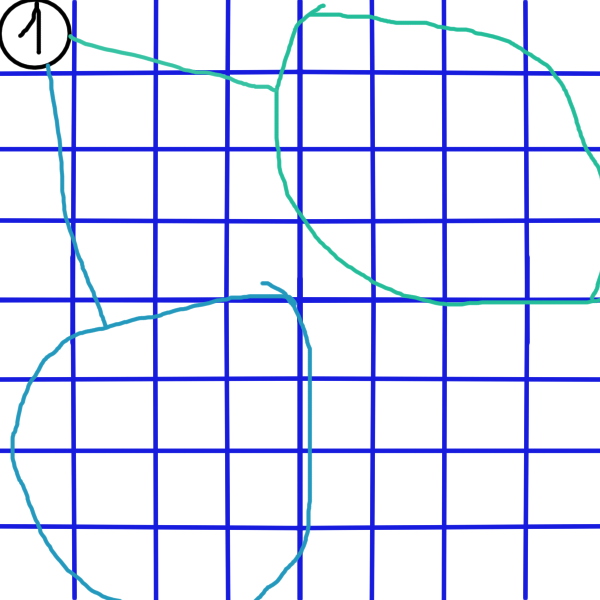
Koreň má najviac dvoch synov. Zjednodušene, prvý podstrom dáme do ľavého dolného, a druhý do pravého horného rohu, ako na obrázku.

Následne všetky obdĺžniky z prvého podstromu nepretínajú druhý podstrom a naopak.

Myšlienka je, položiť podstromy do ich podobdĺžnikov rekurzívne.

Začnime technickými detailami: chceme aby odbdĺžniky na podstromy nezdieľali žiadne \(x\)- any \(y\)- súradnice. To vieme dosiahnuť napríklad tak, že zistíme počet vrcholov v podstrome číslo jedna. Určíme stromu štvorec veľkosti tohto podstromu, končiaci v ľavom dolnom rohu (ako na obrázku). Potom druhému podstromu tiež určíme štvorec zodpovedajúci jeho veľkosti - “ukotvený” v pravom hornom rohu. Keďže súčet veľkostí podstromov je \(n - 1\), použité súradnice sa nebudú prekrývať. V prípade, že vrchol má len jedného syna, podstrom položíme do štvorca so stranou \(n - 1\).

Následne, zavoláme rekurzívnu funkciu na menšie štvorce a položíme do nich podstrom. Pre ilustráciu, pre strom v prvom obrázku dostaneme nasledovný obrázok:

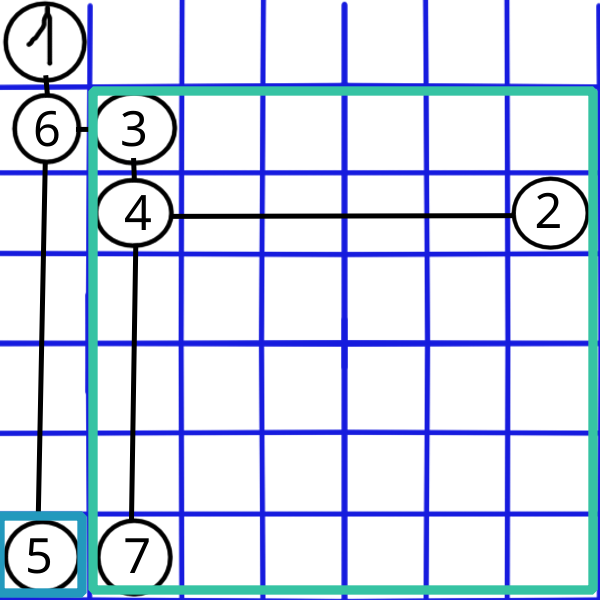
Pri takomto uložení stromu do roviny platí nasledovné. Pre každý vrchol \(v\), všetky vrcholy od neho dohora a doľava sú jeho predkovia (rozmyslite si to). Každý syn je buď viac doprava alebo nižšie ako jeho rodič, takže pre cestu z \(v\) do predka \(p\) nám vždy stačí vziať obdĺžnik s pravým dolným rohom vo \(v\) a ľavým horným rohom v \(p\).

Takéto uloženie stromu do roviny vieme jednoducho implementovať pomocou dvoch DFS (jedno na zistenie veľkostí podstromov a druhé na samotné uloženie stromu) v \(O(n)\) čase aj pamäti.

Všeobecný prípad

Čo v prípade, že se strom nie je binárny? Použijeme podobnú techniku ako pri binárnych stromoch. Avšak, namiesto rozdelenia štvorca na dva podštvorce ho rozdelíme na toľko podštvorcov, koľko má koreň synov, podľa diagonály (ak by sme strom z príkladu hore zakorenili v 6, potom dostaneme rozdelenie ako na ďalšom obrázku).

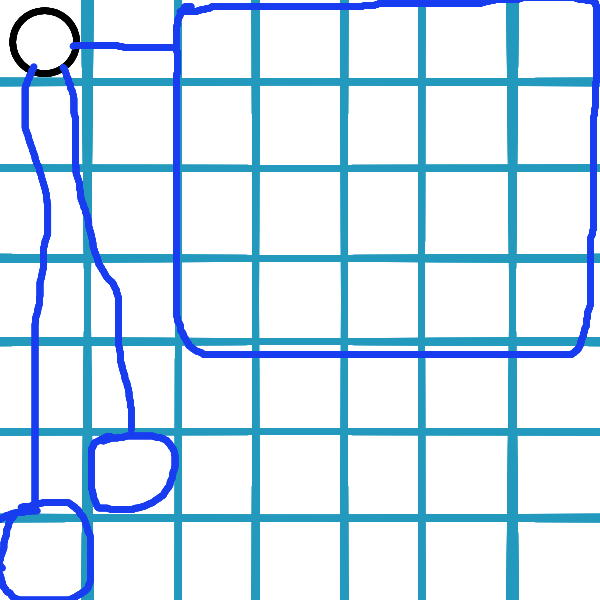
Podštvorce sa nám do štvorca zmenstia, keďže suma veľkostí podstromov je \(n - 1\). Argument, prečo toto položenie do roviny funguje, je veľmi podobný ako pri binárnom strome: zoberme si ľubovoľný vrchol \(v\): všetky vrcholy naľavo hore od \(v\) musia byť jeho predkovia (súrodenci \(v\) a iná rodina je vždy buď napravo alebo dole). Keďže sú položení vo vhodnom poradí (rodič je vždy naľavo hore od detí), každý obdĺžnik s pravým dolným rohom vo vrchole \(v\) obsahuje práve nejakú cestu hore. A naopak, každá cesta hore je položená v obdĺžniku s pravým dolným rohom vo \(v\) a ľavým horným rohom v predkovi.

Toto uloženie stromu do roviny je tiež v lineárnom čase a pamäti.

Ako zodpovedať otázky

Keď už sme strom položili do roviny, prídeme k druhej časti problému. Majme daný pár vrcholov, \(v\) a \(w\) a chceme nájsť dva neprekrývajúce sa obdĺžniky, tak aby pokrývali práve cestu medzi \(v\) a \(w\). Začneme tým, že nájdeme najbližšieho spoločného predka (pozri nižšie). Máme dve možnosti: buď je najbližší spoločný predok jeden z vrcholov \(v\), \(w\) (bez ujmy na všeobecnosti, nech je to \(w\)). Potom vieme položiť celú cestu do jedného obdĺžnika, s pravým dolným rohom vo \(v\) a ľavým horným rohom v \(w\).

Na obrázku je príklad pre \(w = 6\), \(v = 7\):

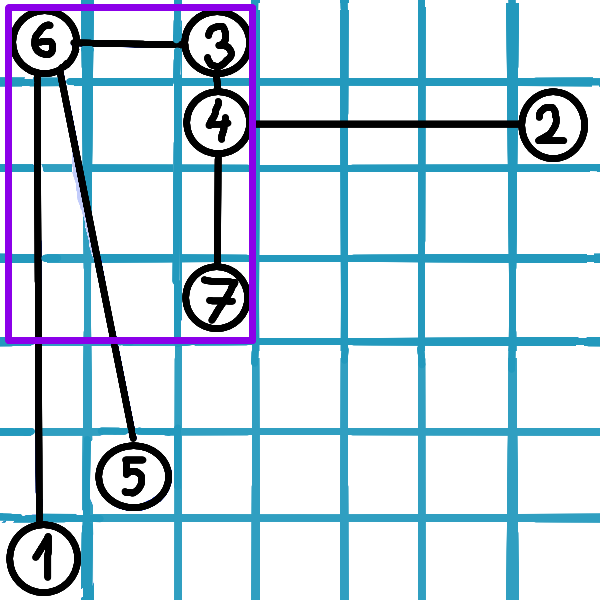
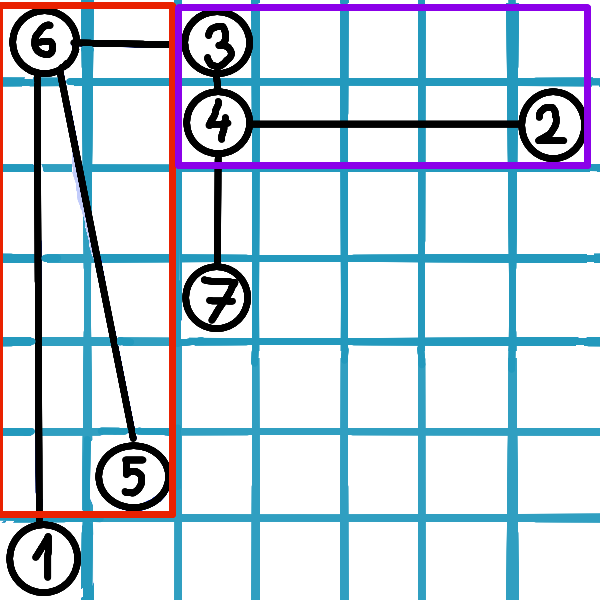
Druhý prípad nastáva, ak najbližší spoločný predok nie je ani \(v\), ani \(w\). Povedzme, že je to nejaký vrchol \(p\). V tom prípade cestu rozdelíme na dve cesty hore: (napríklad) od \(v\) do \(p\) a od \(w\) do jedného zo synov v \(p\). Nemôžeme položiť do obdĺžnikov cesty z \(v\) do \(p\) aj \(w\) do \(p\), pretože potom by mali prekryv. Keď nájdeme vrchol, do ktorého chceme viesť cestu z \(w\), potom už jednoducho získame dva obdĺžniky: jeden má rohy vo \(v\) a \(p\) a druhý v \(w\) a správnom synovi \(w\).

Na obrázku je príklad pre \(v = 5\) a \(w = 2\):

Najbližší spoločný predok

Posledný problém je nájdenie najbližšieho spoločného predka. Najbližší spoločný predok \(v\) a \(w\) je najhlbší taký vrchol (teda najbližší k \(v\) a \(w\)), že jeho podstrom obsahuje oba \(v\) a \(w\).

Naivné hľadanie najbližšieho spoločného predka vyzerá asi takto: (bez ujmy na všeobecnosti, nech \(v\) je hlbší vrchol ako \(w\)) z vrchola \(v\) ideme hore (po rodičoch) kým sa nedostaneme na rovnakú hĺbku, v akej je \(w\). Ak sme takto vošli do vrchola \(w\), potom \(w\) je nabližší spoločný predok. Ak nie, pokračujeme hore, tentoraz posunieme vždy \(v\) a \(w\) naraz, až kým sa nestretnú. Vrchol, v ktorom sa stretnú je najbližší spoločný predok. Toto má časovú zložitosť lineárnu v hĺbke stromu, čo môže byť lineárne v \(n\), takže dostaneme čas \(O(n)\) na query. Toto riešenie nám dá polovicu bodov.

Hľadať to vieme aj rýchlejšie, a to napríklad v čase \(O(\log n)\) na query (pozri kuchárku). V tomto čase vieme nájsť predka o \(k\)-generácií vyššie. Ak vieme hĺbku najbližšieho spoločného predka (označme ju ako \(h_p\), a hĺbky v ktorej sú \(v\) a \(w\) postupne ako \(h_v\) a \(h_w\)), potom do jedného obĺžnika dáme cestu z \(v\) do predka o \(h_v - h_p\) generácií vyššie od \(v\) (najbližšieho spoločného predka) a do druhého cestu z \(w\) do predka \(w\) o \(h_w - h_p - 1\) vyššie (v prípade že najbližší spoločný predok nie je jeden z koncových vrcholov). Rohové body obdĺžnikov teda vieme nájsť v čase \(O(\log n)\) na query, čo nám stačí na plný počet bodov.

#include<bits/stdc++.h>

using namespace std;

const int infinity = 2000000999 / 2;

vector<pair<int, int> > locs;

void set_tomb_location(int ID, int X, int Y) {
    locs[ID] = make_pair(X, Y);
}

vector<vector<int> > hrany;
vector<int> euler, parents, Z;

int dfs_sizes(int v, int f, int h, vector<int> &sizes) {
    Z[v] = euler.size();
    euler.push_back(h);
    parents[v] = f;
    sizes[v] = 1;
    if (hrany.size() != 0) for(int w : hrany[v]) {
        if(w != f) {
            sizes[v] += dfs_sizes(w, v, h + 1, sizes);
            euler.push_back(h);
        }
    }
    return sizes[v];
}

int dfs_build(int v, int f, int x, int y, vector<int> &X, vector<int> &Y, vector<int> &sizes) {
    X[v] = x, Y[v] = y;
    int fur = x;
    int sz = sizes[v] - 1;
    if (hrany.size() != 0) for(int w : hrany[v]) {
        if(w == f) continue;
        sz -= sizes[w];
        fur = dfs_build(w, v, fur + 1, y + sz, X, Y, sizes);
    }
    return fur;
}

struct rmq {
    int n;
    vector<vector<int> > R;
    
    rmq(int m, vector<int> &A) {
        n = m;
        R.push_back(A);
        int jump = 1, id = 0;
        while(jump < n) {
            R.push_back(vector<int>(n));
            for (int i = 1; i < n; i ++) {
                R[id + 1][i] = min(R[id][i], R[id][min(n - 1, i + jump)]);
            }
            jump *= 2;
            id ++;
        }
    }
    rmq() {}
    
    int query(int z, int k) {
        int id = log2(k - z);
        int jump = (1 << id);
        return min(R[id][z], R[id][k - jump]);
    }
};

rmq minis;
vector<vector<int> > minx, miny, maxx, maxy, lca;

void build_tombs(int n){
    vector<int> sizes(n, 0), X(n), Y(n);
    parents.resize(n);
    Z.resize(n);
    dfs_sizes(0, 0, 0, sizes);
    dfs_build(0, 0, 1, 1, X, Y, sizes);
    for(int i = 0; i < n; i ++) set_tomb_location(i, X[i], Y[i]);
    minis = rmq(euler.size(), euler);
    maxy.push_back(Y);
    minx.push_back(X);
    miny.push_back(Y);
    maxx.push_back(X);
    lca.push_back(parents);
    
    int jump = 1, id = 0;
    while(jump < n) {
        maxy.push_back(Y);
        minx.push_back(X);
        miny.push_back(Y);
        maxx.push_back(X);
        lca.push_back(parents);
        
        for(int i = 0; i < n; i ++) {
            lca[id + 1][i] = lca[id][lca[id][i]];
            maxy[id + 1][i] = max(maxy[id][i], maxy[id][lca[id][i]]);
            maxx[id + 1][i] = max(maxx[id][i], maxx[id][lca[id][i]]);
            miny[id + 1][i] = min(miny[id][i], miny[id][lca[id][i]]);
            minx[id + 1][i] = min(minx[id][i], minx[id][lca[id][i]]);
        }
        jump *= 2;
        id ++;
    }
}

void jump_to(int v, int len) {
    int mnx = infinity, mxx = 0, mny = infinity, mxy = 0;
    for(int i = 0; i < minx.size(); i ++) {
        if(len & (1 << i)) {
            mnx = min(minx[i][v], mnx);
            mny = min(miny[i][v], mny);
            mxx = max(maxx[i][v], mxx);
            mxy = max(maxy[i][v], mxy);
            v = lca[i][v];
        }
    }
    cout << mnx << " " << mny << " " << mxx << " " << mxy << "\n";
}

void query(int a, int b){
	int h = minis.query(min(Z[a], Z[b]), max(Z[a], Z[b]) + 1);
    int ha = euler[Z[a]], hb = euler[Z[b]];
    cout << (hb != h ? 2 : 1) << "\n";
    jump_to(a, ha - h + 1);
    if(hb != h) jump_to(b, hb - h);
    fflush(stdout);
}


int main() {
    cin.sync_with_stdio(false);
    cout.sync_with_stdio(false);
    cin.tie();
    cout.tie();
    
    int N;
    cin >> N;
    locs.resize(N);
    hrany.resize(N);
    
    for (int i = 0; i < N - 1; i ++) {
        int a, b;
        cin >> a >> b;
        a --; b --;
        hrany[a].push_back(b);
        hrany[b].push_back(a);
    }
    
    build_tombs(N);
    for(int i = 0; i < N; i ++) {
        cout << locs[i].first << " " << locs[i].second << "\n";
    }
    fflush(stdout);
    
    while(true) {
        int a;
        cin >> a;
        if (a < 1) return 0;
        a --;
        int b;
        cin >> b;
        b --;
        query(a, b);
    }
    
}