Zadanie
Mesto je v karanténe. Všetci sú doma odizolovaní a odlúčení od akejkoľvek ľudskej interakcie. Obyvatelia už dva mesiace nevideli žiaden úsmev, lebo všetky tváre sú zahalené v rúškach. Počasie je ponuré, doma niet čo robiť. Všetci sú v depresii.
Mestská správa však nestráca nádej a rozhodla sa s tým niečo urobiť. Obyvateľstvo by určite rozveselilo trocha motivačnej hudby z rádia. V meste však nie je vysielač, tak treba nejaký postaviť.
Avšak so zvyšujúcou sa vzdialenosťou od vysielača sa zhoršuje signál, a zvyšuje depresia. Presnejšie depresia každého občana je rovná druhej mocnine jeho vzdialenosti od vysielača v metroch.
Aby sa signál mohol lepšie šíriť do všetkých strán a nestáli mu v ceste budovy rozhodli sa ho postaviť na križovatke. Ktorá križovatka však bude najvhodnejšia?
Úloha
Mesto má tvar štvorcovej siete o rozmeroch \(r \times s\). Políčka sú štvorcové pozemky s dĺžkou strany \(8\) metrov. Každý pozemok má súradnice \((i,j)\), je na ňom jeden dom a žije v ňom \(c_{i j}\) ľudí. Pre zjednodušenie predpokladáme, že všetci ľudia sa nachádzajú presne v strede pozemku na ktorom bývajú. V severozápadnom rohu mesta je pozemok so súradnicami \((1,1)\) a v juhovýchodnom \((r,s)\). Medzi pozemkami vedú ulice, ich šírku môžeme zanedbať. Tieto ulice sa pretínajú v \((r + 1) \times (s + 1)\) križovatkách. V severozápadnom rohu mesta je križovatka so súradnicami \((0,0)\), v juhovýchodnom \((r,s)\).
Zistite na ktorej križovatke má mesto postaviť vysielač aby celková depresia jeho obyvateľstva bola najmenšia možná.
Formát vstupu
Na prvom riadku sú dve celé čísla \(r\) a \(s\), oddelené medzerou - rozmery mesta. Platí \(1 \leq r,s \leq 1\,000\) Nasleduje \(r\) riadkov, každý z nich obsahuje \(s\) celých čísel oddelených medzerou. V \(i\)-tom riadku a \(j\)-tom stĺpci je číslo \(c_{i j}\), počet obyvateľov domu na súradniciach \((i,j)\). Platí \(0 \leq c_{i j} \leq 100\,000\).
Je osem testovacích sád. V sadách 1 a 2 naviac platí \(r,s \leq 30\), a v sadách 3, 4 a 5 platí \(r,s \leq 200\).
Formát výstupu
Na prvý riadok vypíšte jedno číslo; najmenšiu dosiahnuteľnú depresiu. Na druhý riadok vypíšte súradnice vysielača, ktoré túto hodnotu dosiahnu. Ak existuje viac riešení vypíšte ľubovoľné z nich.
Výsledok sa nemusí zmestiť do klasickej 32 bitovej číselnej premennej (v C++ preto použite premennú typu long long).
Príklady
Input:
2 3
1 2 2
2 9 1Output:
928
1 1Optimálne je tiež aj \((1,2)\). \(928\) sme dostali ako \(32\cdot(1+2+2+9)+160\cdot(2+1)\)
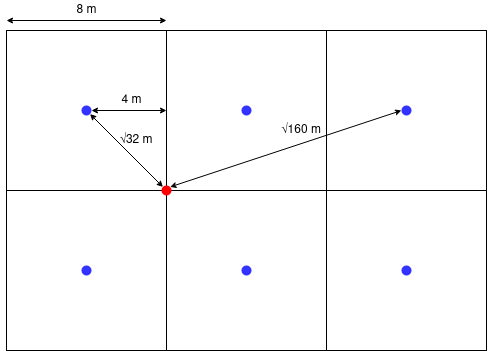
Input:
4 4
0 0 0 2
1 2 5 3
2 0 1 4
1 1 0 0Output:
2880
2 2Aby sme neboli zmätení z označení, vyjasnime si to hneď na začiatku. Zvislá os bude \(x\)-ová, vodorovná bude \(y\)-ová. Políčko na súradniciach \((x, y)\) je teda v riadku \(x\) a stĺpci \(y\).
Hrubá sila
Najpriamočiarejšie riešenie, je riešenie hrubou silou. Skúšame postupne všetkých \((r+1)\cdot(s+1)\) možných súradníc vysielača. Pre každú možnosť prejdeme cez všetkých \(r\cdot s\) domov aby sme spočítali celkovú depresiu.
Časová zložitosť takéhoto riešenia je \(O(r^2s^2)\). Pamäťová zložitosť je \(O(rs)\) (pre každý dom si pamätáme počet obyvateľov).
Rozdelíme si to
Celkovú depresiu pre vysielač na súradniciach \((x,y)\) si vyjadríme takto: \[\sum_{i=1}^{r}\sum_{j=1}^{s}c_{ij}\left((8x-8i+4)^2+(8y-8j+4)^2\right)\] Stačí si uvedomiť, že toto môžeme rozdeliť na dve časti: \[\left(\sum_{i=1}^{r}\sum_{j=1}^{s}c_{ij}(8x-8i+4)^2\right)+\left(\sum_{i=1}^{r}\sum_{j=1}^{s}c_{ij}(8y-8j+4)^2\right)\] Na \(x\)-ovú časť depresie, ktorá závisí iba od \(x\) a nezávisí od \(y\) a na \(y\)-ovú časť, ktorá závisí iba od \(y\). Vďaka tomu môžme hľadať najlepšie \(x\) a \(y\) nezávisle od seba. Inak povedané, nemusíme skúsiť všetky dvojice \((x,y)\), namiesto toho najprv nájdeme najlepšie \(x\) (ktoré minimalizuje \(x\)-ovú časť depresie), a potom najlepšie \(y\).
Takto sme si zlepšili časovú zložitosť na \(O(rs^2+r^2s)\).
Vzorové riešenie
Čo sa týka \(x\)-ovej časti depresie, nerozlišujeme, v akom je dom stĺpci. Záleží nám len na čísle riadka. Všetky domy v tom istom riadku môžme sčítať dokopy. Keď si predpočítame súčty riadkov, budeme môcť počítať \(x\)-ovú časť depresie rýchlejšie. Využijeme teda prefixové súčty. Označme si \(R_i\) súčet počtov obyvateľov domov v riadku \(i\). \(x\)-ová časť depresie teda je: \[\sum_{i=1}^{r}R_i(8x-8i+4)^2\] Pre jedno \(x\) zrátame \(x\)-ovú časť depresie jedným cyklom v čase \(O(r)\). Musíme vyskúšať \(r\) možností, hľadanie najlepšieho \(x\) nám teda tentoraz zaberie \(O(r^2)\)
Samozrejme, rovnaký trik spravíme aj pri počítaní \(y\)-ovej časti depresie. Predpočítame si teda aj súčty stĺpcov.
Časová a pamäťová zložitosť
Časová zložitosť takéhoto riešenia je \(O(r^2+s^2)\). Pamäťová, ak si budeme šikovne počítať súčty riadkov a stĺpcov už pri načítavaní vstupu, je \(O(r+s)\) (nemusíme si držať celé dvojrozmerné pole domov v pamäti).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.