6. Centrifúgy sa dotočia vzorové riešenie

def obsahuje(S, X):
    ps, px = 0, 0
    while True:
        if ps == len(S):
            return True
        if px == len(X):
            return False
        if S[ps] == X[px]:
            ps += 1
            px += 1
        elif ps == 0:
            px += 1
        else:
            ps = 0

bool obsahuje(string S, string X) {
    int ps = 0, px = 0;
    while (true) {
        if (ps == S.length())
            return true;
        if (px == X.length())
            return false;
        if (S[ps] == X[px]) {
            ps += 1;
            px += 1;
        }
        else if (ps == 0) {
            px += 1;
        }
        else {
            ps = 0;
        }
    }
}

AAB

AAAB

CENTRIFUGA

Centrifuga sa nepokazi!

Na začiatku stojí pomerne nemožná úloha – vytvoriť slovo X, ktoré obsahuje a zároveň neobsahuje zadaný reťazec S. Pointa úlohy však spočíva v tom, že kontrola toho, či X obsahuje S je implementovaná zle. Ako prvé je teda potrebné zistiť, kde je problém v zadanej implementácii. Našťastie, k dispozícii máme aj ukážkový vstup, ktorý nefunguje.

def obsahuje(S, X):
    ps, px = 0, 0
    while True:
        if ps == len(S):
            return True
        if px == len(X):
            return False
        if S[ps] == X[px]:
            ps += 1
            px += 1
        elif ps == 0:
            px += 1
        else:
            ps = 0

Prečo vyššie uvedený kód prehlási, že text AAAB neobsahuje AAB? Premenná px označuje pozíciu v reťazci X, ktorú práve kontrolujeme. Premenná ps predstavuje to isté v reťazci S a ukazuje, koľko posledných písmen v X a S sa zhodovalo. Na pozícii px by teda mal končiť reťazec, ktorého posledné písmená sú zhodné s prvými ps písmenami S. Ako je to však v našom prípade?

Zo začiatku všetko ide správne a hodnoty premenných sú px = 2 a ps = 2. To je naozaj správne, prvé dve pozícii X sa zhodujú s prvými dvoma pozíciami S. Ďalšie písmená sa však už nezhodujú, preto program prejde do else podmienky, kde nastaví ps = 0. Pri ďalšej kontrole bude platiť, že S[ps] = X[px] a teda px = 3 a ps = 1. Teda koniec úseku dĺžky tri AAA sa zhoduje so začiatkom slova S dlhým 1, teda A. To je samozrejme pravda, platí však aj silnejšie tvrdenie, že sa zhoduje až s dvoma písmenami S. Hodnota ps by teda mala byť 2.

A to je presne problém tejto implementácie. V tomto okamihu je totiž ps pozadu a už to nemá ako dobehnúť. Pri ďalšom porovnaní správne zhodnotí, že A sa nerovná B, ale znak A porovnáva len preto, že hodnota ps nie je najväčšia možná. To nám napovedá, ako túto úlohu riešiť všeobecne. Zadaný program totiž dokážeme oklamať ak vhodne spojíme dve kópie zadaného slova. Zo začiatku sa bude všetko zhodovať, v nejakom momente, bez toho aby si to program všimol, však prejdeme do druhého slova. V okamihu, keď program nájde chybu, bude už neskoro, pretože sme už prešli začiatok slova S, ktoré sa v X nachádza a program sa už nevie vrátiť.

Ak chceme spojiť dve kópie slova S tak, aby si zadaný program nevšimol, že prešiel z jedného do druhého, najdôležitejšie je zamaskovať prvé písmeno S. Napríklad, ak sa prvé písmeno S v ňom nachádza iba raz, toto sa nám nepodarí a centrifúgu nepokazíme (napr. slovo CENTRIFUGA).

Všeobecný tvar našeho riešenia teda musí vyzerať nasledovne: Majme slovo S, pozíciu \(x\) takú, že S[0] = S[x] a \(y\) je najmenšie také číslo, pre ktoré platí S[y] != S[x+y]. Potom slovo, ktoré dostaneme zreťazením reťazcov S[0:x] (prvých \(x\) písmen slova S) a S, pokazí centrifúgu.

Zadaný program začne spracovávať toto slovo a prvých \(x+y\) písmen sa bude zhodovať. Potom však nájde chybu a nastaví ps = 0. Podľa správnosti by však hodnota ps mala byť \(y\), preto do konca slova nedosiahne ps dostatočnú hodnotu.

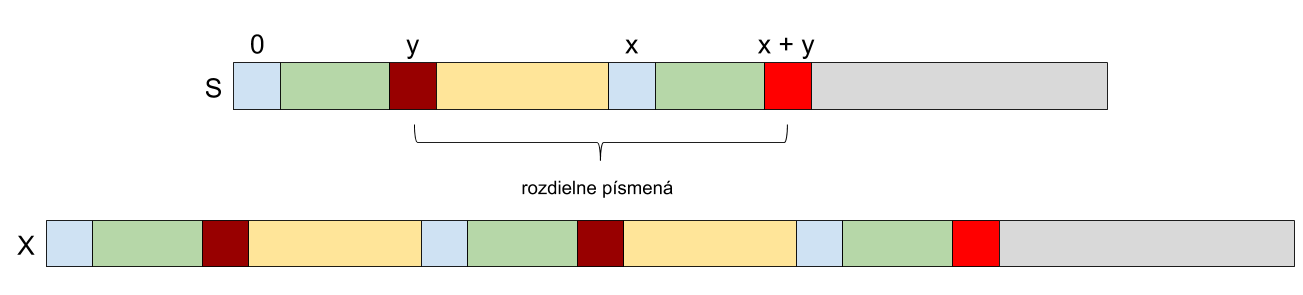
Netreba ešte zabudnúť na to, že zadanie po nás chcelo najkratšie možné slovo. Všimnite si však, že dĺžka slova závisí iba od hodnoty \(x\), tým pádom sa snažíme nájsť čo najmenšie vhodné \(x\), číže prvý vhodný výskyt znaku S[0] v reťazci S (vynímajúc \(x = 0\)).

V tomto momente vieme implementovať jednoduché \(O(n^2)\) riešenie. Postupne vyskúšame každé možné \(x\) také, že S[0] = S[x] a skontrolujeme, či vzniknuté slovo naozaj spôsobí pokazenie centrifúgy. To spravíme buď tak, že nájdeme hodnotu \(y\) takú, že S[y] != S[x+y] alebo proste vložíme vytvorené slovo do funkcie zo zadania. Uvedomme si, že toto overenie je skutočne potrebné, pretože funkcia zo zadania musí v niektorom momente nájsť dva rôzne znaky. Slovo ABAB je príkladom slova, pri ktorom centrifúgu nevieme pokaziť.

K optimálnemu riešeniu nám už chýba iba jedno pozorovanie. V skutočnosti totiž stačí overiť iba prvé \(x > 0\), pre ktoré S[0] = S[x]. Buď sa nám totiž podarí vytvoriť vhodné slovo, a tým pádom máme najkratšie možné riešenie, alebo zistíme, že slovo S je istým spôsobom periodické a úloha preň nemá riešenie.

V tom druhom prípade totiž platí, že S[i] = S[x + i] pre všetky možné \(i\). To ale vynucuje periodickosť slova S, bude totiž platiť aj to, že S[x + i] = S[x + x + i], a teda aj S[i] = S[2x + i]. Tým pádom, rovnaký znak ako je na pozícii 0 je práve na pozíciách S[x], S[2x]… Pre žiadne \(k > 1\) však potom nemôže platiť, že S[0] = S[kx] a zároveň existuje \(y\) také, že S[y] != S[kx + y].

Optimálne riešenie je potom naozaj jednoduché. Stačí nájsť prvú hodnotu \(x > 0\), na ktorej je znak zhodný s prvým písmenom S a overiť, či reťazec S[0:x]S pokazí centrifúgu. Na to nám stačí časová zložitosť \(O(n)\).

s = input()

kde = -1
for i in range(1, len(s)):
    if s[i] == s[0]:
        kde = i
        break

if kde == -1:
    print('Centrifuga sa nepokazi!')
else:
    poz = 0
    while kde + poz < len(s) and s[kde + poz] == s[poz]:
        poz += 1
    if kde + poz == len(s):
        print('Centrifuga sa nepokazi!')
    else:
        print(s[:kde] + s)