Zadanie
Denis sa v lete vybral na brigádu do továrne na kreatívne detské hračky, ktorú vlastní známa americká technologická firma. Zakladatelia tejto značky prišli s nápadom používať pri výrobe hračiek pre deti praktické a život zachráňujúce materiály. Napríklad, časti ich stavebnice sú vyrobené zo špeciálnej hmoty, ktorá pohlcuje radiáciu a tým chráni a lieči deti.
Stavebnica sa skladá z hranolov s rozmermi \(1\,cm\), \(1\,cm\) a \(n\,cm\). Hranoly stavebnice sa ukladajú vždy len rovnobežne na seba, čím vytvárajú akési veže tak, ako je to znázornené na obrázku (pohľad z boku).
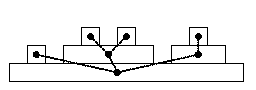
Platia pri tom tieto pravidlá:
- Vrch veže (hranol, na ktorom už nie je položený iný hranol) je kocka s rozmermi \(1\,cm\), \(1\,cm\) a \(1\,cm\).
- Hranol \(a\) položený na hranole \(b\) je kratší než hranol \(b\).
- Medzi podstavami (spodkami) veží je medzera \(1\,cm\).
- Medzi koncom hranola a podstavou veže je \(1\,cm\).
Denis má k dispozícii len istý opis stavebnice. Každý hranol má svoje číslo \(x\) (\(0 \leq x < n\)), pričom \(n\) je počet hranolov v stavebnici. Denis dostane len zoznam \(n-1\) dvojích hranolov \(a\) a \(b\), ktoré sa dotýkajú (jeden je položený na druhom). To sa dá reprezentovať ako stromový graf ako na obrázku, pričom jeho koreň je v najdlhšom hranole a ten má vždy číslo \(0\).
Denisovou úlohou je presne zistiť, koľko centimetrov kubických hmoty je potrebných na výrobu konkrétnej stavebnice. Pomôžete mu?
Formát vstupu
Na prvom riadku vstupu je číslo \(t\) udávajúce počet stavebníc. Nasleduje popis \(t\) stavebníc. Na prvom riadku stavebnice je číslo \(n\), ktoré hovorí o počte hranolov. Nasleduje \(n-1\) dvojíc hranolov \(a\) a \(b\), ktoré znamenajú, že hranoly \(a\) a \(b\) sa dotýkajú.
Platí \(1 \leq t \leq 500\) a \(1 \leq\) súčet \(n \leq 200\,000\).
Formát výstupu
Pre každú stavebnicu vypíšte jedno celé číslo udávajúce objem stavebnice v \(cm^3\) (\(cm^3\) nevypisujte).
Príklady
Input:
2
7
0 1
2 0
0 3
2 4
5 2
6 3
3
1 2
1 0Output:
25
9Na vstupe sú dve stavebnice. Prvá z nich je zobrazená aj na obrázku vyššie. Druhá z nich je jednoduchšia - je to pyramída výšky \(3\), kde najspodnejší hranol \(0\) má dĺžku \(5\), na ňom hranol \(1\) má dĺžku \(3\) a vrchný hranol \(2\) má dĺžku \(1\). To je dokopy objem \(9cm^3\).
Objem, obsah alebo dĺžka?
“Stavebnica sa skladá z hranolov s rozmermi \(1\,cm\), \(1\,cm\) a \(n\,cm\).”
Síce máme zistiť objem staebnice, zaujíma nás len jeden rozmer každého dieliku, keďže tie zvyšné dva sú stále konštantné \(1\,cm\) a \(1\,cm\). Zaujímajú nás teda len dĺžký všetkých hranolov. Tiež vieme, že súčet dĺžok hranolov sa rovná súčtu objemov hranolov, čiže celkovému objemu stavebnice, keďže prierez každého hranolu je štvorec s rozmermi \(1\,cm\) a \(1\,cm\).
Dobre. Aké dĺžky majú hranoly stavebnice? Pripomeňme si pravidlá:
- Vrch veže je kocka s rozmermi \(1\,cm\), \(1\,cm\) a \(1\,cm\).
- Medzi podstavami (spodkami) veží je medzera \(1\,cm\).
- Medzi koncom hranola a podstavou veže je \(1\,cm\).
Príklad
Hranoly si rozdelíme na kocky s rozmermi \(1\,cm\), \(1\,cm\) a \(1\,cm\). Postupne budeme do stavebnice pridávať nové časti a ukážeme si, ako sa podľa toho menia dĺžky hranolov.
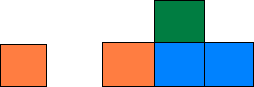
Najprv mala stavebnica len jednu malú vežu, čiže jeden hranol (oranžový) o dĺžke \(1\,cm\). Potom sme ale naň pridali ešte jeden hranol (zelený) a vytvorili tak vežu o výške \(2\). Tým pádom sa spodný hranol predĺžil na \(3\,cm\). Prečo konkrétne?
Predstavme si, že sme najprv priložili zelenú kocku tak, aby vľavo od nej ešte bola medzera \(1\,cm\) na oranžovej kocke. Tým pádom je z ľavej strany splnené tretie pravidlo - medzi koncom spodného hranol a zeleným hranolom je \(1\,cm\).
Zelená kocka by teraz ale levitovala vo vzduchu, pod ňou by ostalo prázdne miesto. Preto pod celú dĺžku zleného hranola dáme modré kocky. A aby sme splnili tretie pravidlo aj z pravej strany, pridáme ešte jednu kocku vpravo.
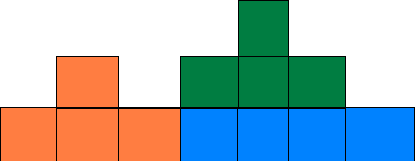
Teraz sa v stavebnici objavila nová (zelená) veža. Je uložená na už existujúcom hranole (oranžový), ktorý sa predĺžil o modrú časť. Všimnime si, že modrá časť má dlžku zase šírky podstavy novej veže a jednu krajnú kocku naviac.
Dĺžka hranola
Takže akú dlžku má hranol stavebnice? Vždy aspoň \(1\,cm\). Pre každý hranol na ňom prirátame jeho dĺžku a \(1\,cm\) za kocku vpravo, aby medzi koncom spodného a horného hranola bola medzera \(1\,cm\) alebo aby existovala medzera \(1\,cm\) medzi dvoma susednými vežami. Z toho nám teda vychádza akýsi vzorec: 1 + súčet dĺžok podstáv (šírok) veží + počet veží.
Ak si túto stavebnicu predstavíme ako strom, kde každý vrchol je jeden hranol stavebnice, a rozdelíme si ho na podstromy, tak šírka každého podstromu závisí od jeho podstromov. Každý podstrom reprezentujúci vežu má nejakú šírku, čiže dĺžku hranola v jeho koreni – dĺžku podstavy.
Rekurzia
Keďže vo “vzorci” na výpočet dĺžky jedného hranola používame šírky veží na ňom (dĺžky ďalších hranolov), ktoré závisia od dĺžok ďalších hranolov nad nimi atď., vidíme tu akýsi rekurzívny princíp.
Na to aby sme zistili dĺžku koreňa nejakého podstromu, musíme najprv zrátať dĺžky jeho synov a ich synov atď.
Táto rekurzia ale musí mať konečnú hĺbku. Pre ktoré hranoly/vrcholy vieme určiť ich dĺžku bez potreby spúšťania ďalšej rekurzie? Hmm… Listy tohto stromu, čiže vrcholy veží, majú vždy dĺžku \(1\,cm\). To sedí aj podľa nešho vzorca. Ak na hranole nie sú žiadne ďalšie hranoly, má dĺžku \(1\,cm\).
Keďže je zaručené, že graf stavebnice na vstupe bude strom, a vieme, že každý strom určite má listy, máme istotu, že vytvorená rekurzia sa nezacyklí.
Zložitosti
Takouto rekurziou (alebo prehľadávaním stromu do hĺbky) navštívime každý vrchol práve raz, čiže časová zložitosť tohto riešenia je tak lineárna \(O(n)\), kde \(n\) je počet vrcholov grafu, počet hranolov v stavebnici.
Pamäťová zložitosť tohto riešenia je tiež lineárna \(O(n)\), keďže nám stačí pamätať si zoznam susedov pre daný graf. Vieme, že strom s \(n\) vrcholmi má \(n - 1\) hrán.
#include <cstdio>
#include <vector>
using namespace std;
vector <vector <int> > Edge;
long long result;
long long dfs(int node, int parent) {
int size = 0;
for (int i : Edge[node])
if (i != parent)
size += dfs(i, node);
result += size + Edge[node].size();
return size + Edge[node].size();
}
int main() {
int t;
scanf("%d", &t);
for (int j = 0; j < t; j++) {
int n;
scanf("%d", &n);
Edge.resize(n);
Edge.clear();
for (int i = 0; i < n - 1; i++) {
int a, b;
scanf("%d %d", &a, &b);
Edge[a].push_back(b);
Edge[b].push_back(a);
}
result = 0;
dfs(0, -1);
printf("%lld\n", result + 1);
}
}Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.