6. Totálna pohroma (vzorové riešenie) - Korešpondenčný seminár z programovania

Zadanie

Syseľ sa s hlbokým výdychom zvalil na svoju kancelársku stoličku. Hotovo! Po mesiacoch úpornej driny sa mu konečne podarilo dokončiť samofunkčný vysávač poháňaný jadrovým reaktorom. Jediný vysávač takéhoto druhu na celom svete. Proste unikát.

Bol položený na stole pred ním, chrómované telo odrážalo svetlo, trubica vedúca zo stredu sa pomaly otáčala a snažila sa nájsť špinu na vysatie, to všetko doplnené jemným bzukotom reaktora. A všade naokolo papiere, nákresy, výpočty, kusy kódu. Naprogramovať umelú inteligenciu bola pre Sysľa hračka, konštrukcia vysávača tiež nebola problematická. Reaktor mu však dal zabrať. Ani by ste netušili, aký je problém zohnať dostatočné množstvo kvalitného uránu. Ale ani keď ho len tak hodíte do vnútra, tak to nezačne fungovať. Lietajúce neutróny treba celý čas precízne kontrolovať, jednak aby jadrová reakcia nevyhasla, jednak aby to celé nevybuchlo.

Tajomstvom je použitie špeciálnej kontrolnej matice rozmerov \(n \times n\), cez ktorú neutróny filtrujete. Každé políčko je buď priepustné alebo nepriepustné, je však dôležité, aby platilo, že v každom štvorci okolo hlavnej diagonály je práve párny počet nepriepustných políčok. Presnejšie, ak si ľavý horný roh matice označíte súradnicami \((1, 1)\) a pravý dolný súradnicami \((n, n)\), tak musí platiť, že každý štvorec, ktorého protiľahlé rohy sú na súradniciach \((i, i)\) a \((j, j)\) (pre \(i < j\)) má párne veľa nepriepustných políčok. Syseľ pohľadom zavadil o nákres tejto kontrolnej matice, ktorý ležal pred ním na stole. Asi by ho mal niekam odložiť, predsa je to len najdôležitejšia časť jeho výtvoru a on si ju ešte nestihol zálohovať.

V tom však do miestnosti vstúpila ona a Syseľ zabudol na všetko ostatné. Nikol. Najlepšia programátorka v celom VacuumLabs. Keby ste ju videli ako píše na svojej ergonomickej klávesnici. Prsty sa jej len tak mihajú po klávesách. A keď potom spraví pull request, pozerať sa naňho chodia ešte aj z Exponei. K tomu všetkému je ešte aj nesmierne krásna a nezadaná. Len nedávno sa síce rozišla so svojím priateľom¹, ale je najvyšší čas, aby Syseľ spravil prvý krok. A jadrový vysávač môže byť presne tá vec, ktorá ju ohúri.

Keď Nikol vošla do miestnosti, Syseľ sa v okamžiku postavil zo stoličky, aby ju privítal. Pritom však na stôl vysypal omrvinky z keksíkov, ktoré jedol počas práce. Jeho inteligentný vysávač to hneď zaregistroval a začal otáčať trubicu aby ich vysal. Pritom však omylom prevrhol pohár vody a tá sa rozliala po nákrese kontrolnej matice. Katastrofa! Ako teraz Syseľ ohúri Nikol, keď je jeho výtvor zničený? Na mokrom papieri je vidno už iba niekoľko 0 a 1, ktoré predstavujú priepustné a nepriepustné políčka. Pomôžte Sysľovi zistiť, koľkými spôsobmi vie doplniť zvyšok matice, nech sa môže pustiť do opravovania.

Úloha

Na vstupe dostanete veľkosť matice \(n\) a políčka, ktoré ostali zachované spolu s ich pôvodnými hodnotami – 0 alebo 1. Zistite, koľkými spôsobmi je možné doplniť zvyšné políčka tejto matice číslami 0 a 1 tak, aby platilo, že v každom štvorci okolo hlavnej diagonály so stranou väčšou ako 1 je párne veľa jednotiek.

Hlavná diagonála matice je tvorená políčkami, pre ktoré platí, že ich \(x\)-ová a \(y\)-ová súradnica je rovnaká. Ťahá sa preto od ľavého horného rohu (súradnice \((1, 1)\)) k pravému dolnému rohu (súradnice \((n, n)\)). Štvorec je okolo hlavnej diagonály vtedy, ak dva jeho protiľahlé rohy ležia na hlavnej diagonále.

Keďže počet spôsobov, ako doplniť maticu, môže byť naozaj veľký, vypíšte iba ich zvyšok po delení číslom \(1\,000\,000\,009\).

Formát vstupu

Na prvom riadku vstupu sa nachádzajú dve celé čísla \(n\) a \(m\) (\(2 \leq n \leq 10^5\), \(0 \leq m \leq min(50\,000, n^2)\)) – veľkosť matice a počet zachovaných políčok.

Nasleduje \(m\) riadkov, každý popisuje jedno zachované políčko pomocou troch čísel \(x_i\), \(y_i\) a \(c_i\) (\(1 \leq x_i, y_i \leq n\), \(0 \leq c_i \leq 1\)) – súradnice tohto políčka a jeho hodnota. Je zaručené, že jedno políčko sa môže objaviť na najviac jednom riadku vstupu.

Testovacie vstupy pre túto úlohu sú rozdelené do 8 sád, pre ktoré platia nasledovné dodatočné obmedzenia:

V sade 1 platí, že \(n = m\) a všetky zadané políčka ležia na hlavnej diagonále. Inými slovami, máte presne zadané ako vyzerá hlavná diagonála a nič naviac.
V sade 2 a 3 platí, že \(n \leq m\) a medzi zadanými políčkami sa vyskytujú všetky políčka na hlavnej diagonále. Oproti vstupm zo sady 1 teda máte aj zadaných aj niekoľko dodatočných políčok.
V sade 4 platí, že \(n \leq 20\).
V zvyšných sadách neplatia žiadne dodatočné obmedzenia.

Formát výstupu

Na výstup vypíšte jedno celé číslo – počet možností, ktorými je možné doplniť maticu \(n \times n\) číslami 0 a 1 tak, aby platila zadaná podmienka. Toto číslo vypíšte modulo \(1\,000\,000\,009\).

Príklad

Input:

Output:

Všetky možné doplnenia sú uvedené na nasledovnom obrázku:

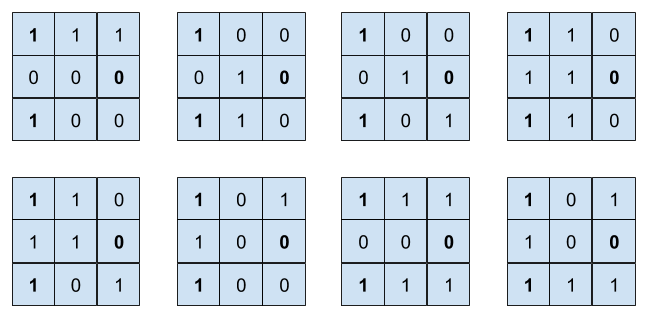
Input:

Output:

Ak do stredného políčka dopíšeme 0, štvorec \(2\times 2\) v ľavom hornom rohu nebude mať párne veľa jednotiek. A ak do stredného políčka dopíšeme 1, zlý bude pravý dolný \(2 \times 2\) štvorec.

Bol to hlupák, ak chcete počuť Sysľov názor.↩

Úloha vyzerá už na prvý pohľad komplikovane. Máme počítať počet možností, niektoré časti sú už vopred určené a tie dopĺňať nemáme a popritom ešte máme kontrolovať, že v každom diagonálnom štvorci bude párny počet jednotiek. Keďže je toho veľa, treba sa skúsiť zamerať na nejakú menšiu časť, objaviť niekoľko základných pravidiel a odtiaľ sa posúvať k všeobecnému riešeniu. A samozrejme celý čas si kresliť, to pomáha najviac. Nuž a keď sme si nie istý, ktorým smerom sa vydať, pomôcť nám môžu návodné, ľahšie, sady.

Hlavná diagonála našej matice je dôležitá, keďže nás zaujímajú iba štvorce v jej okolí. V prvej sade navyše máme zaručené, že všetky prvky tejto diagonály sú vopred určené a nič naviac sme nedostali. Pokúsme sa teda postupne vypĺňať zvyšné políčka. Začať môžeme od najmenších možných štvorcov veľkosti \(2\times 2\). V tomto prípade máme určené dve políčka na diagonále a doplniť treba zvyšné dve. Vieme, že súčet týchto prvkov musí byť párny (čo je len inak vyjadrená podmienka párneho počtu jednotiek), čísla z diagonály nám teda určujú či sú zvyšné dve čísla rovnaké alebo rozdielne.

Predstavme si, že súčet dvoch zadaných čísel na diagonále je párny. Potom aj zvyšné dve čísla musia mať párny súčet – musia byť rovnaké. Naopak, ak čísla na diagonále dávajú nepárny súčet, sú rôzne, musia byť rôzne aj zvyšné dve čísla. V oboch prípadoch máme dve možnosti, ako tieto hodnoty doplniť. V párnom prípade to bude buď \(0-0\) alebo \(1-1\), v nepárnom buď \(0-1\) alebo \(1-0\) (na poradí záleží, keďže sú to rôzne políčka matice).

Našťastie, je jedno, ktorú možnosť si zvolíme, pri zvyšných štvorcoch to nemôže zavážiť. Môžete si totiž všimnúť, že ľubovoľný diagonálny štvorec, ktorý obsahuje jedno z týchto dvoch políčok musí nutne obsahovať aj druhé. No a ich súčet je určený diagonálnym štvorcom \(2 \times 2\) a je jedno, ktorými hodnotami sa k tomuto súčtu dopracujeme. Do výsledku si teda môžeme poznačiť, že sme získali dve rôzne možnosti a pokračovať ďalej s ľubovoľnou z nich.

Po doplnení štvorcov \(2 \times 2\) sa presunieme na štvorce \(3 \times 3\). Opäť nám na doplnenie ostávajú už len dve hodnoty – rohy neležiace na hlavnej diagonále. Zvyšné políčka sú totiž zahrnuté v niektorom menšom diagonálnom štvorci. Zo súčtu už vyplnených políčok opäť zistíme, či má byť súčet týchto políčok párny alebo nepárny, teda či sú v nich čísla rovnaké alebo rôzne. Z toho opäť vyplývajú dve možné priradenia hodnôt, ktoré sú však ekvivalentné a je jedno, ktoré z nich si zvolíme, stačí že si zapamätáme, že sme mali dve možnosti na výber.

Vieme si však všimnúť zaujímavú vec. V skutočnosti je parita súčtu dvoch nedoplnených políčok rovnaká ako parita stredného políčka štvorca \(3\times 3\). Prečo? Všimnime si, že všetky už doplnené políčka sa dajú rozdeliť do dvoch diagonálnych štvorcov veľkosti \(2 \times 2\), ktoré sa prekrývajú v strednom políčku, označme si ho \(x\). Súčet prvkov všetkých týchto políčok sa rovná súčtu oboch štvorcov \(2\times 2\) mínus \(x\), ktoré sme započítali dvakrát. Ale súčet prvkov v štvorci \(2 \times 2\) musí byť párny. To znamená, že výsledný súčet musí mať rovnakú paritu ako hodnota \(x\). Rohy štvorca \(3\times 3\) teda vieme doplniť iba na základe streného čísla, ktoré sa nachádza na hlavnej diagonále.

Pokúsme sa doplniť prvky v diagonálnych štvorcoch \(k \times k\), pričom \(k > 3\) a všetky menšie štvorce sú úspešne vyplnené. Opäť vidíme, že nevyplnené ostávajú iba dve políčka v rohoch tohto štvorca. Naviac, vyplnené políčka tvoria dva diagonálne štvorce veľkosti \((k-1) \times (k-1)\), ktoré sa prekrývajú v diagonálnom štvorci veľkosti \((k-2) \times (k-2)\). Súčet týchto prvkov vieme teda vypočítať aj tak, že sčítame súčet štvorcov s hranou \(k-1\) a odčítame súčet štvorca s hranou \((k-2)\). Súčty všetkých týchto štvorcov musia byť však podľa zadania párne. To znamená, že aj tento výsledok bude párny. Z toho vyplýva, že hodnoty v nediagonálnych rohoch štvorca \(k \times k\) musia byť rovnaké a navyše vôbec nezávisia od hodnôt na diagonále ani ničom inom.

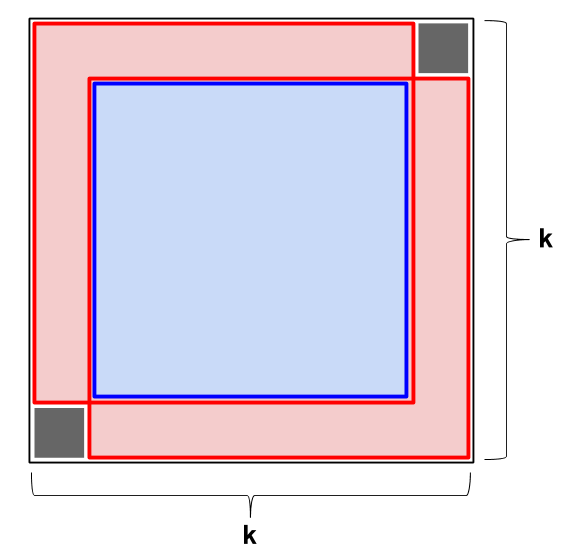
Sivé políčka ešte nie sú vyplnené. Červené aj modré štvorce musia obsahovať párny počet 1. Z toho vyplýva, že počet 1 v celom štvorci s výnimkou sivých políčok je párny. Sivé políčka teda musia obsahovať rovnakú hodnotu.

Tento prístup nefunguje pre štvorce \(3\times 3\) a \(2\times 2\), pretože menšie štvorce, z ktorých sa skladajú, nie sú veľkosti aspoň \(2\times 2\), a tým pádom pre ne neplatí predpoklad o párnosti ich súčtu.

Z vyššie uvedených tvrdení vidíme, že v okamihu keď máme vyplnenú diagonálu, riešenie je jednoduché. Políčka symetrické cez diagonálu sú od seba navzájom závislé, v prípade, že sú od diagonály príliš vzidalené musia mať rovnakú hodnotu, inak sú hodnotami na diagonále mierne ovplyvnené. V každom prípade však dostaneme dve možnosti ich hodnôt, a preto výsledok musí byť \(2^{\frac{n^2 - n}{2}}\) – mimo diagonály je \(n^2 - n\) políčok a ich hodnoty určujeme po dvojiciach.

Toto číslo vieme vypočítať metódou rýchleho umocňovania v čase \(O(\log n)\). Myšlienka tohto algoritmu je rekurzívna. Namiesto toho aby sme mocninu počítali postupným násobením číslom \(2\), počítame hodnotu \(2^a\) tak, že rekurzívne spočítame číslo \(2^{a/2}\), ktoré potom umocníme na druhú. Namiesto postupného počítania všetkých hodnôt \(2, 2^2, 2^3, 2^4 \dots 2^{a-2}, 2^{a-1}, 2^a\) budeme počítať iba hodnoty \(2^a, 2^{a/2}, 2^{a/4} \dots 2^2, 2\), ktorých je výrazne menej, iba logaritmicky veľa.

V druhej sade sme okrem celej diagonály mali vyplnené aj nejaké ďalšie políčka. Ako to ovplyvní výsledok? Obmedzí to naše možnosti. Všetky možné doplnenia sa totiž vyskytovali v dvojiciach, napríklad sme mohli zistiť, že konkrétne dve políčka musia byť rovnaké, teda buď \(0-0\) alebo \(1-1\). Ak však máme určené, že jedno z týchto políčok má hodnotu 0, tak nám ostáva iba jedna možnosť. Navyše, ak by sme v takomto prípade zistili, že obe políčka sú predvyplnené rozdielnymi hodnotami, vieme, že maticu nevieme doplniť žiadnym spôsobom.

V tomto prípade musíme rozlišovať dva prípady podľa vzdialenosti zadaného políčka od hlavnej diagonály. Pre políčka, ktoré sú priďaleko, aspoň vo vzdialenosti 3 od diagonály nám stačí overiť, či nemáme zadané aj pre ne symetrické políčko s opačnom hodnotou. V takom prípade bude teda možných doplnený 0, inak započítame iba jednu, vstupom určenú, možnosť pre túto dvojicu políčok. Najjednoduchšie riešenie tohto problému je použitím binárneho vyhľadávacieho stromu (set v C++), ktoré ale vedia k riešeniu s časovou zložitosťou \(O(m\log m)\). Toho logaritmu sa však vieme zbaviť, či už použitím hash mapy alebo nejakého rýchlejšieho triedenia, napr. radix sort. Pri programovaní však takýto malý rozdiel zvyčajne nepotrebujeme riešiť, keďže set je skutočne rýchly.

Zadané políčka v blízkosti diagonály sú o niečo dôležitejšie, sú totiž ovplyvnené hodnotami na diagonále a nevieme dopredu povedať, či majú byť symetrické políčka rozdielne alebo rovnaké. Potrebujeme ich teda prejsť samostatne. Navyše, s týmito hodnotami budeme musieť oveľa viac pracovať aj v prípade, že diagonála nie je určená, preto si ich treba vhodne zapamätať. Pomôcť nám môže buď hash mapa, ale takisto sa dá použiť klasické pole, keďže si potrebujeme pamätať iba 5 diagonál – hlavnú a po dvoch susedných na oboch strán.

Zatiaľ sme riešili iba problém, v ktorom boli hodnoty na diagonále vopred určené. Toto však nie je všeobecný prípad. Ako si s ním teda poradíme?

Nuž, budeme si ju musieť určiť. Samozrejme, mohli by sme ju určovať celú naraz, v takom prípade by sme museli prejsť postupne každú z \(2^n\) možností. Uvedomme si však, že na diagonále závisia iba štvorce veľkosti \(2\times 2\) a \(3\times 3\). To znamená, že hodnoty na spodku diagonály nijak neurčujú, ako majú vyzerať hodnoty na jej vrchu. Presnejšie, políčka na diagonále, ktoré sú od seba vo vzdialenosti viac ako 3 sa už vôbec neovplyvňujú.

Na riešenie teda použijeme dynamické programovanie. Väčšinou keď počítate počet možností, riešením bude nejaká verzia dynamického programovania. Stav nášho dynamického programovania bude \(D_{k,x,y}\) – koľkými možnosťami vieme vyplniť diagonálne štvorce veľkosti \(2\times 2\) a \(3\times 3\) v štvorci začínajúcom na políčku \((0,0)\) a končiacom na políčku \((k,k)\) ak posledné dve hodnoty na diagonále budú \(x\) a \(y\)?

Výpočet tejto hodnoty bude závisieť na tom, ako sme vyplnili o jedno menší štvorec, teda od hodnôt \(D_{k-1, 0, x}\) a \(D_{k-1, 1, x}\). V tomto prípade nás zaujíma iba to, koľkými možnosťami vieme doplniť políčka \((k-1, k)\), \((k-2, k)\), \((k, k-1)\) a \((k, k-2)\), keďže vyplnenie zvyšných políčok bolo určené hodnotami \(D_{k-1, z, x}\).

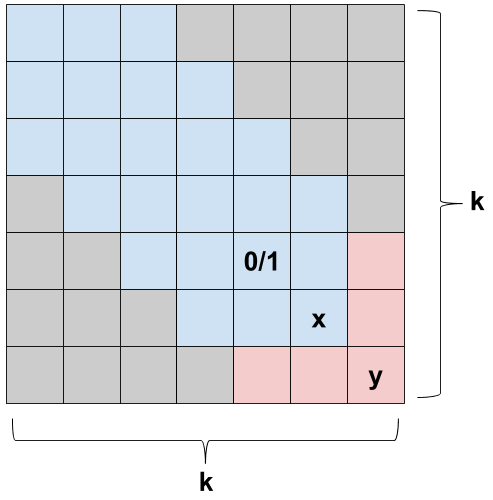
Sivé políčka nás nezaujímajú, pretože sú od diagonály priďaleko. Aktuálne doplňané políčka sú červené. Modré boli vyplnené v predchádzajúcich iteráciách dynamického programovania a poznáme pre ne počet rôznych možností. Na diagonále sme si určili hodnoty \(x\) a \(y\), ktoré ovplyvňujú aktuálne počítané políčka. Pri tretej hodnote vyskúšame obe možnosti, aj 0 aj 1.

Toto overenie je navyše jednoduché, stačí sa pozrieť, či sú určené hodnoty kompatibilné s hodnotami, ktoré máme zadané na vstupe, hodnoty niektorých z týchto políčok totiž už môžu byť doplnené, a vrátiť jednu z hodnôt 0, 1 alebo 2.

Hodnotu jedného stavu dynamického programovania vieme vypočítať v konštantnom čase a všetkých stavov je \(4n\). Celková časová zložitosť tohto kroku je preto \(O(n)\). Celková časová zložitosť tohto riešenia je \(O(n + m)\), pamäťová \(O(n + m)\). Pred programovaním je ešte treba poriadne si rozmyslieť okrajové prípady, začiatok dynamického programovania a rozobrať krok samotnej dynamiky. Potom je to však pomerne priamočiare.

#include <cstdio>
#include <iostream>
#include <string>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <set>
#include <map>
#include <stack>
using namespace std;

#define For(i,n) for(int i=0; i<(n); i++)
#define mp(a,b) make_pair((a),(b))
typedef long long ll;
typedef pair<int,int> pii;

ll MOD = 1000000009ll;
map<pii, int> M;

int vratM(int x, int y) {
    if (M.count({x, y}) == 0)
        return -1;
    return M[{x, y}];
}

ll moznosti_2x2(int k, int x, int y) {
    // hodnoty na diagonale su ine
    if ((vratM(k, k) != -1 && vratM(k, k) != y)
            || (vratM(k-1, k-1) != -1 && vratM(k-1, k-1) != x)) return 0;
    // rohove policka nie su zadane
    if (vratM(k, k-1) == -1 && vratM(k-1, k) == -1) return 2;
    // prave jedno rohove policko je zadane
    if (vratM(k, k-1) == -1 || vratM(k-1, k) == -1) return 1;
    // obe rohove policka su zadane
    return 1 - (x + y + vratM(k, k-1) + vratM(k-1, k))%2;
}

ll moznosti_3x3(int k, int x) {
    // rohove policka nie su zadane
    if (vratM(k, k-2) == -1 && vratM(k-2, k) == -1) return 2;
    // prave jedno rohove policko je zadane
    if (vratM(k, k-2) == -1 || vratM(k-2, k) == -1) return 1;
    // obe rohove policka su zadane
    return 1 - (x + vratM(k, k-2) + vratM(k-2, k))%2;
}

// vrat hodnotu a^b
ll umocni(ll a, ll b) {
    if (b == 0) return 1;
    if (b%2 == 1) return (a * umocni(a, b-1)) % MOD;
    ll p = umocni(a, b/2);
    return (p * p) % MOD;
}

ll D[100047][2][2];

int main() {
    int n, m;
    scanf(" %d %d", &n, &m);
    For(i, m) {
        int x, y, w;
        scanf(" %d %d %d", &x, &y, &w);
        M[{x-1, y-1}] = w;
    }
    if (n == 1) {
        if (vratM(0, 0) == -1) printf("2\n");
        else printf("1\n");
        return 0;
    }
    // dynamicke programovanie
    For(x, 2) For(y, 2) D[1][x][y] = moznosti_2x2(1, x, y);
    for (int k = 2; k < n; k++) {
        For(x, 2) For(y, 2) {
            D[k][x][y] = ((D[k-1][0][x] + D[k-1][1][x]) * moznosti_2x2(k, x, y) * moznosti_3x3(k, x)) % MOD;
        }
    }
    // pocet policok mimo 3x3 stvorcov
    ll pocet = (ll)n * n - 5*(n-2) - 4;
    ll jed = 0, dvoj = 0;
    for (auto it = M.begin(); it != M.end(); it++) {
        int x = it->first.first, y = it->first.second, w = it->second;
        // v niektorom 3x3 stvorci
        if (abs(x - y) < 3) continue;
        if (vratM(y, x) == -1) jed++;
        else {
            dvoj++;
            if (w != vratM(y, x)) {
                printf("0\n");
                return 0;
            }
        }
    }
    // spocitanie vysledku
    pocet -= dvoj + 2*jed;
    pocet /= 2;
    ll vysledok = 0;
    For(x, 2) For(y, 2) vysledok += D[n-1][x][y];
    vysledok *= umocni(2, pocet);
    vysledok %= MOD;
    printf("%lld\n", vysledok);
}

Diskusia

Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.

Pre pridávanie komentárov sa musíš prihlásiť.

6. Totálna pohroma vzorové riešenie