4. Treba sa najesť vzorové riešenie

3
haha
ha
zabajezaba
zaba
kamen
ak

ano
nie
nie

Predtým než sa ponoríme do riešenia, zaveďme si notácie zľahčujúce zápis niektorých vzťahov. A[i:j] je súvislý úsek reťazca A, ktorý začína na \(i\)-tom písmene a končí na \(j\)-tom písmene (použitý zápis teda zodpovedá polootvorenému intervalu). Tu treba zdôrazniť fakt, že ľavý index sa berie vrátane, ale pravý index sa neberie. Navyše, ak vynecháme ľavý index, znamená to začiatok slova a vynechanie pravého indexu znamená koniec slova. Teda A[:] je v tomto prípade celý reťazec A¹. Okrem toho, ak povieme, že A sa zmestí do B, budeme tým myslieť to, že A je podreťazcom B. Posledné dôležité výrazy, ktoré možno už poznáte, sú prefix a suffix. Prefix označuje súvislú časť reťazca, ktorá začína na jeho začiatku, teda A[:i] a suffix označuje súvislú časť reťazca, ktorá končí na jeho konci, teda A[i:].

Začnime si ujasnením toho, čo musí platiť pre dvojicu reťazcov S a T, pre ktoré je odpoveď ano. Vieme, že každý znak z S na pozícii \(i\) (pre \(0 \leq i < |S|\)) sa musí nachádzať v nejakom podreťazci tvoriacom T. To znamená, že musí existovať také \(j\), že \(j\)-ty znak v T je rovnaký ako \(i\)-ty znak v S a zároveň sa T[:j] zmestí do S[:i] a T[j+1:] sa zmestí do S[i+1:].

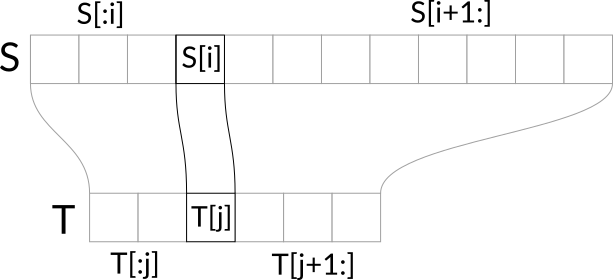
Ako prvé by sme si teda mohli rozmyslieť, ako overiť, že sa reťazec A zmestí do reťazca B. To je však pomerne jednoduché. Postupne budeme prechádzať reťazcom B, pričom si pamätáme index do A, ktorý nám hovorí, ako dlhý prefix A sme už v B videli. Počiatočná hodnota tohto indexu je, samozrejme, 0. Ak narazíme v B na znak, ktorý sa zhoduje s písmenom na tomto indexe v A, posunieme index o jedna ďalej. A na konci reťazca B iba overíme, že sme prešli celým A. Časová zložitosť tohto postupu je lineárne závislá od dĺžky B. To je však príliš pomalé, ak to chceme robiť pre každú dvojicu znakov v S a T.

My si však dokážeme takúto informáciu získať aj rýchlejšie, a to dynamickým programovaním. Musíme si totiž uvedomiť, že naše otázky sa netýkajú náhodných reťazcov. Zakaždým sa pýtame iba na to, či sa nejaký prefix T zmestí do prefixu S (a rovnako so sufixami). Pre každý prefix S by sme si mohli predpočítať, aký najdlhší prefix T sa doň zmestí. Jednak vďaka tomu vieme odpovedať na ľubovoľnú otázku, lebo dlhšie prefixy sa určite nezmestia a všetky kratšie sa zmestiť musia, a jednak vieme tieto hodnoty počítať v jednom prechode a to práve spomínaným dynamickým programovaním.

Ak je T[:j] podreťazcom S[:i], potom určite bude T[:j] aj podreťazcom S[:i+1], pretože sme len pridali písmeno. Ale naviac, ak sa S[i] rovnalo T[j], tak vieme, že aj T[:j+1] je podreťazcom S[:i+1]. Rovnakým postupom ako predtým, pomocou jedného indexu do T si teda vieme predpočítať pole, ktoré nám pre ľubovoľný prefix S povie, aký najdlhší prefix T sa doň zmestí. Toto isté, akurát odzadu, vieme spraviť aj pre suffixy. Teraz už vieme ľahko zistiť, či sa T[:j] nachádza v S[:i], stačí sa pozrieť, aký najdlhší prefix T sa zmestí do S[:i], čo máme predpočítané v poli, a porovnať ho s \(j\).

V tomto bode máme riešenie s časovou zložitosťou \(O(|S| \cdot |T|)\). Pre každý index \(i\) v reťazci S vyskúšame každý možný index \(j\) v T a overíme, či sú tieto znaky rovnaké a či sa zvyšok reťazca T zmestí do príslušných častí S, čo pomocou predpočítaných hodnôt vieme robiť v konštantnom čase. Predpočítanie hodnôt však trvá iba \(O(|T|)\) a ich používanie konštantný čas, najpomalšia časť riešenia je teda tá, kde pre znak z S zisťujeme, ktorý znak z T mu priradiť. Túto časť by sme teda chceli urýchliť.

Majme \(i\)-ty znak z \(S\) a najdlhší možný prefix, ktorý sa zmestí do S[:i] je T[:j]. To znamená, že \(i\)-ty znak musí zodpovedať niektorému z prvých \(j+1\) znakov \(T\), inak by sa zvyšný prefix T do S[:i] nezmestil. Nech je teda \(i\)-ty znak napríklad x. Potom tento znak musí zodpovedať niektorému x z prvých \(j+1\) znakov reťazca T. Uvedomme si však, že je vhodné vybrať čo najneskorší výskyt x v T[:j+1]. Prefix² totiž bude stále vyhovovať, a čím väčšiu hodnotu si vyberieme, tým kratší suffix stačí dať do S[i+1:]. To znamená, že ak sa \(i\)-ty znak z S nachádza v nejakej podpostupnosti tvoriacej T, tak to musí byť aj v prípade, keď je toto \(i\)-te písmeno najpravejší výskyt v T[:j+1].

Chceli by sme preto vedieť rýchlo odpovedať na otázku: Ktorá najpravejšia pozícia T[:j] obsahuje písmeno \(x\)? Pre každé písmeno si vytvoríme pole dĺžky \(|T|\), kde na pozícii \(k\) bude posledná pozícia daného písmena v prefixe T dĺžky \(k\). To sa počíta ľahko, keďže buď je táto hodnota rovnaká ako znak predtým, alebo je to hodnota aktuálnej pozície, ak je na nej hľadaný znak.

Časová zložitosť predpočítania polí je lineárna od dĺžky reťazca S a časová zložitosť počítania výskytov písmen je lineárna od dĺžky reťazca T a dĺžky abecedy (v tomto prípade ju môžeme považovať za konštantu 26). Nakoniec netreba zabudnúť na počet vstupov \(n\). Výsledná časová zložitosť je \(O(n \cdot (|S| + |T|))\). Pamätať si potrebujeme iba dve polia dĺžky \(|S|\) a 26 polí dĺžky \(|T|\) a táto informácia nazáleží na počte vstupov, pamäťová zložitosť je teda \(O(|S| + |T|)\).

#include <cstdio>
#include <iostream>
#include <string>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <set>
#include <map>
#include <stack>
using namespace std;

#define For(i,n) for(int i=0; i<(n); i++)
#define mp(a,b) make_pair((a),(b))
typedef long long ll;
typedef pair<int,int> pii;

int main2() {
    char C[200047];
    scanf(" %s",C);
    string s = C;
    scanf(" %s",C);
    string t = C;
    vector<vector<int> > Pp(26), Ps(26);
    For(i, 26) {
        Pp[i].resize(t.length()+1);
        Pp[i][0] = -1;
        Ps[i].resize(t.length()+1);
        Ps[i][t.length()] = t.length();
    }
    For(i, t.length()) {
        For(j, 26) Pp[j][i+1] = Pp[j][i];
        Pp[t[i] - 'a'][i+1] = i;
    }
    for(int i = t.length()-1; i >=0; i--) {
        For(j, 26) Ps[j][i] = Ps[j][i+1];
        Ps[t[i] - 'a'][i] = i;
    }
    vector<int> P(s.length()),S(s.length());
    int index = 0;
    For(i, s.length()) {
        if(index != t.length() && s[i] == t[index]) index++;
        P[i] = index;
    }
    index = t.length()-1;
    for(int i = s.length()-1; i >= 0; i--) {
        if(index != -1 && s[i] == t[index]) index--;
        S[i] = index + 1;
    }
    bool res = true;
    For(i, s.length()) {
        int left = Pp[s[i] - 'a'][P[i]], right = Ps[s[i] - 'a'][S[i]];
        if(left < right) res = false;
    }
    if(res) printf("ano\n");
    else printf("nie\n");
}

int main() {
    int t;
    scanf("%d", &t);
    For(i, t) main2();
}