6. Optimalizácia písania na klávesnici vzorové riešenie

3 7
autobus
auto
autostrada
auto
aut
a
autobusar
autobus
autob
utobus

1
2
1
5
3
2
6

Pred tým než sa pustíme do vzoráku si ujasnime niekoľko pojmov:

• Reťazec (angl. string) je postupnosť znakov. Môže to byť slovo, jeho časť ale aj celá veta.

• Prefix je začiatočný úsek reťazca. Formálnejšie, reťazec \(a\) nazveme prefixom reťazca \(b\), ak za \(a\) vieme dopísať niekoľko (možno aj nula) znakov tak, aby sme dostali reťazec \(b\). Napríklad reťazec auto má päť prefixov – "" (prázdny reťazec), a, au, aut a auto.

Pri písaní zadaného slova nás zaujíma iba to, čo máme aktuálne napísané. Tento reťazec reprezentuje nejaký stav, v ktorom sa nachádzame. Stlačením klávesy sa náš reťazec zmení a my sa presunieme do iného stavu. Napríklad ak sú v slovníku slová autobus a autostrada, tak ak sa nachádzame v stave au, môžeme sa jedným stlačením presunúť do nasledovných stavov:

• aut, tým, že stlačíme t (za t si môžeme dosadiť ľubovoľné písmeno, stlačením l by sme sa dostali do stavu aul a podobne)
• autobus, tým že stlačíme TAB, automaticky sa nám doplní lexikograficky najmenšie slovo zo slovníka, ktoré začína na au
• a, tým že stlačíme Backspace zmažeme posledný znak

V okamihu ako nám v úlohe vystupujú stavy, medzi ktorými sa presúvame, môžeme sa na ne pozrieť ako na graf. Stavy reprezentujú jednotlivé vrcholy a presun zo stavu do stavu orientovanú hranu. To zásadne zmení aj úlohu, ktorú riešime. V pôvodnom zadaní sme chceli vedieť, ako čo najrýchlejšie dostať z prázdneho reťazca reťazec výsledný. Prázdnemu aj výslednému reťazcu však teraz zodpovedajú nejaké vrcholy a nás zaujíma najkratšia cesta medzi nimi.

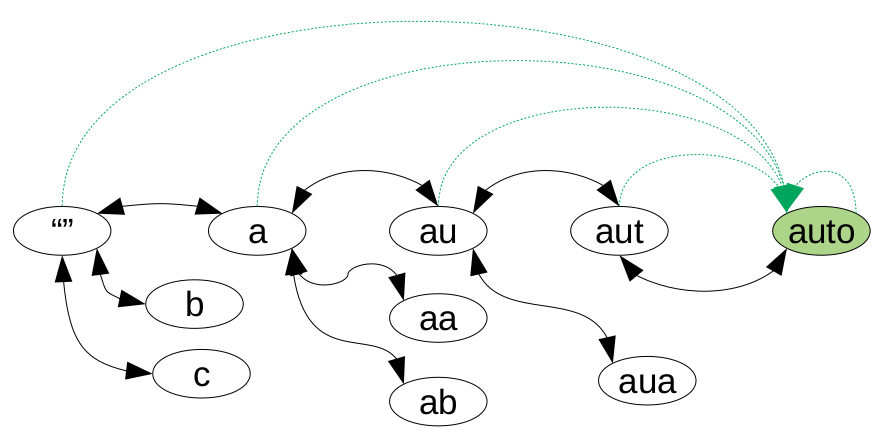
Na obrázku môžeme vidieť, ako by vyzerala časť grafu so slovom auto. Skutočný graf je totiž nekonečný a obsahuje všetky možné reťazce. Všimnite si, že čierne šipky sú obojsmerné. To značí možnosť dopísania písmena na koniec a jeho vymazania stlačením Backspace. Tiež si všimnite zelené šípky, ktoré predstavujú stláčanie klávesy TAB.

Povedali sme si, že písanie slova je ekvivalentné hľadaniu najkratšej cesty medzi zadanými vrcholmi. Takže môžeme využiť dobre známy algoritmus prehľadávania do šírky (BFS). Problémom ale je, že náš graf je nekonečný, keďže na klávesnici vieme napísať čokoľvek. Pokúsme sa teda zmenšiť počet stavov, ktorými sa musíme zaoberať.

Kľúčovým pozorovaním je, že si nepotrebujeme pamätať stavy, ktoré nie sú prefixom žiadného slova v slovníku.

Prečo je tomu tak? Keby sme na písanie mohli používať iba písmená, úloha by bola jednoduchá, lebo cestu by sme si nevedeli nijak skracovať a museli by sme proste napísať zadané slovo písmeno po písmene. Nám však pribudli aj klávesy TAB a Backspace. A klávesa TAB dopĺňa slová zo slovníku, ktoré majú rovnaký prefix ako reťazec, ktorý sme doposiaľ napísali. Ak sme teda v stave, ktorý nie je prefixom žiadneho slova v slovníku, klávesa TAB nič nerobí.

Klávesa Backspace má tiež len obmedzené využitie. Uvedomme si, že v optimálnom riešením nikdy nepoužijeme Backspace tesne po tom, čo napíšeme nejaké písmeno. Keby sme to totiž spravili, reťazec by sa vlastne nezmenil a my by sme tieto dve stlačenia mohli radšej vynechať. Backspace teda môžeme stlačiť iba po nejakom TAB alebo Backspace. To znamená, že vymazávanie znakov využijeme iba v prípade, že stlačíme TAB, doplnené slovo však bude pridlhé a niekoľko posledných znakov budeme chcieť vymazať. Pri tom všetkom sme sa však neustále pohybovali po reťazcoch, ktoré sú prefixami slov v slovníku.

Z vyššie uvedených pozorovaní tiež vyplýva, že v okamihu ako sa rozhodneme opustiť prefixy slov v slovníku, tak klávesy TAB a Backspace už nemá zmysel použiť a nám ostáva zvyšný text dopísať písmeno po písmene.

Keď si teda predstavíme ako funguje naše riešenie, ak chceme napísať slovo \(s\), tak najskôr sa budeme pohybovať po prefixoch slova \(s\), ktoré sú zároveň prefixami niektorých slov v slovníku a keď tieto prefixy opustíme, zvyšok slova \(s\) jednoducho dopíšeme.

Na obrázku vidíme, ako vyzerá graf všetkých prefixov slov zo slovníka auto, autobus a autostrada.

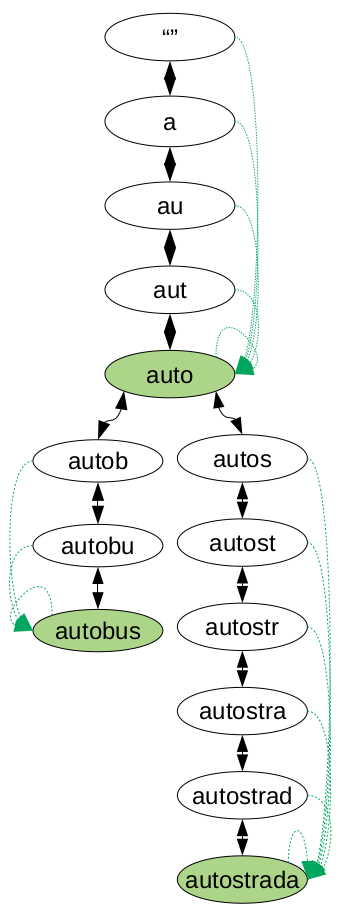
Skúsený riešiteľ si isto všimne, že graf ktorý nám ostane pripomína písmenkový strom (po anglicky aj trie). Písmenkový strom je dátová štruktúra, v ktorej si pamätáme informácie o slovách v slovníku a ich prefixoch. Každý vrchol reprezentuje konkrétny prefix slova v nej – presne ako v grafe ktorý vytvárame. Z každého vrcholu vedie najviac 26 hrán do synov – vrcholov, ktoré reprezentujú stavy do ktorých sa dostaneme pridaním jedného písmenka na koniec reťazca. My si však do tohto písmenkového stromu ešte musíme pridať hrany, ktoré reprezentujú stláčanie kláves TAB a Backspace.

Písmenkový strom sa tradične konštruuje tak, že začíname s prázdnym stromom, do ktorého postupne pridávame slová. Slovo pridávame po písmenách začnúc v koreni. Postupne sa snažíme posúvať po hranách, ktoré reprezentujú jednotlivé písmená slova. V okamihu, keď sa chceme posunúť po hrane, ktorá ešte z aktuálneho vrcholu nevedie, vytvoríme nový vrchol a do neho vedúcu hranu. Pri vytváraní vrcholu môžeme veľmi jednoducho spraviť hranu aj pre Backspace – stačí si zapamätať otca vrcholu.

Hrany pre autocomplete sú najzložitejšie, vieme ich však vygenerovať rekurzívne. Ak vrchol reprezentuje slovo v slovníku tak jeho autocomplete vedie do neho samého. Ak nie, tak pre každého syna najprv rekurzívne zistíme jeho autocomplete a potom vyberieme autocomplete zo syna, do ktorého vedie hrana s lexikograficky najmenším písmenom v abecede.

Po skompletizovaní grafu na ňom spustíme prehľadávanie do šírky, ktoré nám pre každý vrchol vypočíta, ako najrýchlejšie sa do neho vieme dostať zo začiatku, ktorý reprezentuje prázdny reťazec, a tieto hodnoty si zapamätáme.

Ostáva nám už len odpovedať na otázku, ako najrýchlejšie vieme napísať slovo \(s\). Na to nájdeme najdlhší prefix tohto slova, ktorý sa nachádza aj v našom písmenkovom strome. Z predpočítanej informácie vieme, ako najrýchlejšie napísať tento prefix a keďže je to prefix najdlhší, zvyšok už aj tak musíme napísať písmeno po písmene.

Časová zložitosť konštruovania je lineárna od súčtu dĺžok slov v slovníku. BFS tiež spravíme v lineárnom čase od počtu vrcholov v strome. A nájsť najdlhší prefix tiež zvládneme v čase lineárnom od dĺžky hľadaného slova. Celková časová zložitosť je teda lineárna od dĺžky vstupu. Pamäťová zložitosť je lineárna od počtu vrcholov v písmenkovom strome. Naviac, táto zložitosť je určite optimálna, keďže rovnako veľa času nám zaberie načítanie celého vstupu.

#include<cstdio>
#include<vector>
#include<string>
#include<queue>
#include<cstring> //strlens
#include<algorithm> // min
#include<utility> //pair
#include<iostream> //cin
#include<cassert> //assert
using namespace std;
int charToInt(char c) //zmeni znak na cislo
{
    return c-'a';
}
struct pismenkac
{
    vector<pismenkac *> V;
    int vzdOdKorena = -1;
    pismenkac *TAB, *rodic;
    
    //konstruktor -> skonstruuj novy vrchol, a pridaj do neho slovo c
    pismenkac(const char * c, pismenkac * _rodic)
    {
        V.resize(26,nullptr);
        TAB = nullptr;
        rodic = _rodic;
        
        if(*c == '\0') {TAB=this; return;}
        V[charToInt(*c)]=new pismenkac(c+1, this);
    }
    
    pismenkac()
    {
        V.resize(26,nullptr);
        TAB = nullptr;
        rodic = nullptr;
    }
    
    //pridaj slovo
    void pridajSlovo(const char *c)
    {
        if(*c == '\0')
        {
            //ak sa v tomto vrchole konci slovo
            TAB=this;
        } 
        else if(V[charToInt(*c)]) // treba pridat zvysok slova
            V[charToInt(*c)]->pridajSlovo(c+1); 
        else //treba vytvorit vrchol do ktoreho pridame zvysok slova
            V[charToInt(*c)] = new pismenkac(c+1, this); 
    }
    
    void doplnTABlinky()
    {
        for(auto &x: V)
            if(x)
                x->doplnTABlinky();
        if(!TAB)
            for(auto &x: V)
            {
                if(x)
                {
                    TAB = x->TAB;
                    return;
                }
            }
    }
    
    //zisti ako daleko je slovo od korena, c je zostavajuci suffix - este nespracovane pismena zo stromu
    int najdiSlovo(const char *c){
        if(*c=='\0') //ak sme nasli slovo
            return vzdOdKorena;
        if(V[charToInt(*c)] == nullptr) //ak zvysok slova nie je v grafe
            return strlen(c)+vzdOdKorena; //scitame vzdialenost tohto vrchola od korenu a dlzku zvysku slova
        return V[charToInt(*c)]->najdiSlovo(c+1); //pokracuj v hladani hladaneho slova/prefixu u syna
    }
};

//vyrataj BFS
void BFS(pismenkac * begin)
{
  queue<pismenkac *> Q;
  Q.push(begin); //v Q budu iba vrcholy ktore este neboli spracovane a budu spracovane v najblizsej iteracii
  begin->vzdOdKorena = 0;
  while(Q.size())
  {
      pismenkac * kde = Q.front(); // vrchol
      
      int vzd = kde->vzdOdKorena;
      Q.pop();
      
      if(kde->TAB->vzdOdKorena == -1) //chod po hrane TAB linky
      {
         kde->TAB->vzdOdKorena = vzd+1;
         Q.push(kde->TAB);
      }
      if(kde->rodic && kde->rodic->vzdOdKorena == -1) //chod po hrane Backspace k rodicovi
      {
         kde->rodic->vzdOdKorena = vzd+1;
         Q.push(kde->rodic);
      }
      for(auto &p : kde->V) //chod po hrane pismenka
      {
          if(p && p->vzdOdKorena == -1)
            {
                p->vzdOdKorena = vzd+1;
                Q.push(p);
            }
      }
  }
}

int main()
{
    string slovo;
    pismenkac p;
    int n, q;
    cin>>n>>q;
    while(n--)
    {
        cin>>slovo;
        p.pridajSlovo(slovo.c_str());
    }
    p.doplnTABlinky();
    BFS(&p);
    while(q--)
    {
        cin>>slovo;
        cout<<p.najdiSlovo(slovo.c_str())<<endl;
    }
}