5. Prestavba bytu vzorové riešenie

Zadanie

Krtko rekonštruuje byt. Posledné, čo mu zostáva je vydláždiť novú kúpeľňu. Zhodou náhod sa mu v schránke objavil leták obľúbeného veľkoskladu - Kúpeľňového Sveta Podláh - a v ňom zľava na dlaždice L-kového tvaru. Táto ponuka bola natoľko lákavá, že Krtko nakúpil oveľa viac dlaždíc, ako potreboval. Teraz sedí pred svojou dokonalou dokonalo-štvorcovou kúpeľňou a premýšľa, či on vôbec bude vedieť pomocou týchto kachličiek svoju kúpeľňu vydláždiť. Akoby nestačilo, v jeho inak príjemne dokonalo-štvorcovej kúpeľni sa nachádza otvor na odtok sprchy, ktorý nemôže kachličkami prekryť. Pomôžte Krtkovi vydláždiť jeho kúpeľňu alebo zistite, že to nie je možné.

Úloha

Štvorcovú kúpeľňu si môžeme predstaviť ako štvorcovú sieť \(n \times n\). Pre dokonalo štvorcovú kúpeľňu navyše platí, že veľkosť jej strany \(n\) je mocnina dvojky. Odtok zaberá v myslenej sieti práve jedno celé políčko. Pod dlaždicou L-kového tvaru myslíme tri štvorce veľkosti \(1 \times 1\), spojené do tvaru L.

Vykachličkovanie je možné, ak pomocou L-kových kachličiek vieme prekryť všetky voľné miesta v našej kúpeľni (okrem odtoku) bez toho, aby sme nejaké kachličky akokoľvek delili alebo ľubovolne prekrývali. Taktiež sa nesmie stať, že by nejaká kachlička vyčnievala z kúpeľne. Samozrejme, nakúpené kachličky je možné akokoľvek otáčať. Kachlička teda môže byť orientovaná 4 rôznymi spôsobmi.

Na vstupe od nás dostanete veľkosť kúpeľne. Ďalej od nás dostanete pozíciu odtoku. Ak je možné kúpeľňu takýchto rozmerov s odtokom na danom mieste vykachličkovať iba pomocou nakúpených L-kových kachličiek, vypíšte ľubovolné takéto vykachličkovanie. Ak to možné nie je, podajte o tom správu.

Formát vstupu

Na prvom riadku vstupu sa nachádza číslo \(n\) \((1 \leq n \leq 256)\) – dĺžka hrany štvorca reprezentujúceho kúpeľňu, pričom platí, že \(n\) je mocnina 2. V ďalšom riadku nasleduje dvojica čísel \(r, s\) \((1 \leq r, s \leq n)\) – číslo riadku a stĺpca v našej mriežke, kde sa nachádza odtok.

Formát výstupu

Ak vykachličkovanie nie je možné, vypíšte na jeden riadok výstupu reťazec Neda sa. Inak si označme všetky použité kachličky číslami od 1 do \(x\), kde \(x\) je ich počet (je zrejmé, že \(x = (n^2-1) \div 3\)). Na výstup vypíšte \(n\) riadkov. V každom takomto riadku sa má nachádzať \(n\) medzerou oddelených reťazcov. Ako \(j\)-ty reťazec v \(i\)-tom riadku vypíšte číslo kachličky, ktorá prekrýva poličko v \(i\)-tom riadku a \(j\)-tom stĺpci mriežky alebo vypíšte znak X ak sa na danom políčku nachádza odtok. Korektných riešení môže byť viac (napríklad prečíslovaním kachličiek dostaneme z jedného korektného riešenia iné korektné riešenie). Vypíšte ktorékoľvek z nich.

Hodnotenie

Vaše riešenia budú testované na štyroch sadách testovacích vstupov, pre ktoré platí:

Sada	1	2	3	4
\[ 1 \leq n \leq \]	\(4\)	\(16\)	\(64\)	\(256\)

Príklady

Input:

2
1 1

Output:

X 1
1 1

Kúpeľna veľkosti \(2 \times 2\) s odtokom v ľavom hornom rohu. Je len jedno možné riešenie.

Input:

4
2 3

Output:

2 2 1 1
2 3 X 1
4 3 3 5
4 4 5 5

Jedno z možných riešení. Akékoľvek iné riešenie s iným prečíslovaním či inou pozíciou kachličiek bude tiež akceptované.

Zadanie tejto úlohy bolo pomerne priamočiare. Máme zadanú štvorcovú mriežku nejakých špeciálnych rozmerov a máme ju celú okrem jedného daného políčka vykachličkovať veľa kachličkami tvaru L.

Riešenie hrubou silou

Prvé riešenie, ktoré môžeme vyskúšať pokiaľ nevieme s ničím lepším prísť, je riešenie hrubou silou, teda skúšanie všetkých možností. V tomto prípade ale nie je úplne jasné, ako takéto skúšanie pekne a dobre implementovať. Ako teda v tomto prípade rozumne postupovať?

Začneme tým, že asi najprirodzenejšou reprezentáciou podlahy kúpeľne je klasické dvojrozmerné pole. To chceme vyplniť číslami kachličiek a následne ho vypísať na výstup. Ďalej vieme už vopred povedať, koľko kachličiek použijeme: stačí si vypočítať počet políčok, odrátať jedno za odtok a vydeliť tromi. Ostáva teda už len zistiť, ako majú byť jednotlivé kachličky otočené a rozmiestnené.

Chceli by sme teraz vymyslieť nejaký systematický postup skúšania všetkých možností. Vezmime si nejaké políčko, ktoré ešte nie je pokryté kachličkou (a ani odtokom). Toto políčko musíme nejako pokryť. Kedže máme iba malý (a hlavne konečný) počet možností, ako to spraviť, môžeme postupne vyskúšať všetky. Presnejšie, budeme postupovať nasledovne: vždy si vyberieme nejakú možnosť, ako toto políčko pokryť, tú si zaznačíme do poľa a rekurzívne sa zavoláme (“vyskúšaj všetky možnosti ako dokončiť toto aktuálne kachličkovanie”). Ak sa z rekurzie vrátime s tým, že žiadne riešenie sme nenašli, odstránime z poľa zaznačený spôsob pokrytia aktuálneho políčka a prejdeme na ďalšiu možnosť, ako ho pokryť.

Naše konkrétne riešenie bude prechádzať pole systematicky: zhora dole a v rámci riadku zľava doprava. Zakaždým, keď nájdeme prázdne políčko, spravíme preň vyššie popísaný postup, pričom pri rekurzívnom volaní si odovzdáme súradnice, kde sme boli, aby sme vedeli, odkiaľ ďalej stačí hľadať nasledujúce voľné políčko. Jeden možný stav počas behu tohto riešenia je znázornený na nasledujúcom obrázku:

Akými možnými spôsobmi ide vo všeobecnosti takéto políčko pokryť? Pri našom systematickom postupe máme zaručené, že všetky políčka v skorších riadkoch aj všetky políčka v aktuálnom riadku naľavo od práve pokrývaného sú už pokryté. Stačí nám teda vyskúšať nanajvýš štyri možnosti, a to tieto:

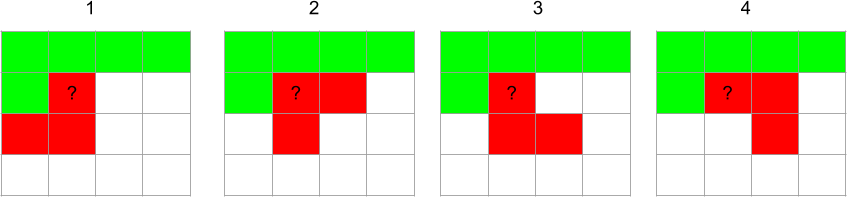
Na implementáciu tohto riešenia nám stačí jedna funkcia, ktorá ako parametre dostane súradnice prvého políčka (v nami zvolenom poradí), ktoré sme ešte neskontrolovali. Pri každom volaní skontrolujeme jedno políčko. Ak už je pokryté, alebo je to odtok, len sa zavoláme na nasledujúce. Ak nie, tak vyskúšame všetky štyri možnosti, ako ho pokryť, a pre každú, ktorá naozaj pasuje, sa rekurzívne zavoláme na nasledujúce políčko. No a akonáhle sa dostaneme k tomu, že úspešne skontrolujeme, že posledné políčko v poslednom riadku je pokryté, môžeme vyhlásiť, že sme našli riešenie.

Táto funkcia tiež musí mať prístup k poľu, do ktorého zostrojujeme popis kachličkovania. Toto sa dá riešiť rôznymi spôsobmi, napríklad tak, že si referenciu na pole budeme odovzdávať ako ďalší parameter našej rekurzívnej funkcie. (Treba si dať pozor na to, aby sme nekopírovali celé pole pri každom rekurzívnom volaní.)

Technika pre skúšanie všetkých možností, ktorú sme si práve popísali, je známa pod menom backtracking. Pamäťová zložitosť tohto riešenia je zjavne \(O(n^2)\), kedže nám stačí pamätať si iba aktuálne pokrytie mriežky, ktoré sa práve pokúšame doplniť. Časová zložitosť môže byť v najhoršom prípade rádovo až \(O(4^{(n^2/3)})\) kedže pri prikladaní každej kachličky máme na výber nanajvýš 4 možnosti.

#include <iostream>
#include <vector>

using namespace std;

vector<pair<int, int> > otoc1 = { {0, 0}, {1, 0}, {1, -1} };
vector<pair<int, int> > otoc2 = { {0, 0}, {1, 0}, {1, 1} };
vector<pair<int, int> > otoc3 = { {0, 0}, {0, 1}, {1, 0} };
vector<pair<int, int> > otoc4 = { {0, 0}, {0, 1}, {1, 1} };

vector<vector<pair<int, int> > > otocenia = {otoc1, otoc2, otoc3, otoc4};

////////////////////////////////////////

bool hotovo = false;
int n;
vector<vector<int> > kupel;

////////////////////////////////////////

bool preoznac(int i, int j, int k, int oznacenie)
// preoznaci L-ko typu k na policku (i, j)
// oznacujem vyjadruje ci oznacujem alebo premazavam policka
{
    bool oznacujem = true;
    if(kupel[i][j] != 0) oznacujem = false;
    
    for(int a=0;a<3;++a)
    // skontrolujeme, ci vieme preoznacit vsetky 3 policka
    {
        int di, dj;
        di = i + otocenia[k][a].first;
        dj = j + otocenia[k][a].second;
        
        if(di < 0 || dj < 0 || di >= n || dj >= n) return false;
        
        if(oznacujem && kupel[di][dj] != 0) return false;
        else if(!oznacujem && kupel[di][dj] != oznacenie) return false;
    }
    
    for(int a=0;a<3;++a)
    {
        int di, dj;
        di = i + otocenia[k][a].first;
        dj = j + otocenia[k][a].second;
        
        if(oznacujem) kupel[di][dj] = oznacenie;
        else kupel[di][dj] = 0; 
    }
    
    return true;
}

bool f(int i, int j, int ozn)
{
    if(hotovo) return true;
    
    if(j == n)
    // pokazila sa nam indexacia v riadku, presuvame sa na dalsi alebo koncime
    {
        if(i == n-1)
        {
            hotovo = true;
            return true;
        }
        else return f(i+1, 0, ozn);
    }

    if(kupel[i][j] != 0)
    // uz je zaplnene, posuvame sa
    {
        return f(i, j+1, ozn);
    }
    
    for(int k=0;k<4;++k) if(!hotovo)
    {
        if( !preoznac(i, j, k, ozn) ) continue;
        
        if( f(i, j+1, ozn+1) ) return true;
        
        preoznac(i, j, k, ozn);
    }
    
    return false;
}

int main()
{
    int a, b;
    cin >> n >> a >> b;
    
    kupel.resize(n, vector<int>(n, 0));
    kupel[a-1][b-1] = -1;
    
    f(0, 0, 1);
    
    for(int i=0;i<n;++i)
    {
        for(int j=0;j<n;++j)
        {
            if(j != 0) cout << " ";
            
            if(kupel[i][j] == -1) cout << 'X';
            else cout << kupel[i][j];
        }
        cout << "\n";
    }
    
    return 0;
}

Niektoré implementácie tohto riešenia však fungujú v skutočnosti prekvapivo dobre. Riešenie totiž nielen že vždy existuje, je ich dokonca tak veľa, že sa často stane, že už prvá možnosť priloženia kachličky, ktorú vyskúšame, vedie k riešeniu – a tak skutočné skúšanie možností budeme robiť až pri okrajoch, kde už niektoré umiestnenia kachličiek budú robiť problémy.

Vzorové riešenie

Ako by sme mohli začať hľadať nejaké riešenie, ktoré bude zaručene efektívne? Dobrým začiatkom je skúsiť ručne vyriešiť nejaké mriežky menších rozmerov a získať tak trochu obraz o tom, ako riešenia vyzerajú a pre ktoré kombinácie (veľkosť mriežky, poloha odtoku) riešenie neexistuje.

Ak sa pozrieme na mriežky veľkosti \(2\times 2\) či \(4\times 4\), zistíme, že nech je odtok kdekoľvek vždy nájdeme nejaké riešenie. To by nám mohlo napovedať, že by to mohlo ísť aj pre úplne všetky väčšie mriežky – len budeme musieť náš postup nejak zovšeobecniť.

Skúsme sa pozrieť napríklad na to, ako vieme vykachličkovať mriežku veľkosti \(4\times 4\) s odtokom v ľavom hornom rohu. Ľahko zistíme, že vieme doložiť jednu kachličku tak, aby sme doplnili celý ľavý horný štvorec veľkosti \(2\times 2\). Ako teraz pokryť ostatné tri štvorce rozmerov \(2\times 2\)? Každý z nich by sme vedeli pokryť samostatne, ak by obsahoval odtok. Inými slovami, každý z nich vieme pokryť celý okrem jedného jeho políčka. A už sme skoro vyhrali. Všimnite si kachličku, ktorá je na nasledujúcom obrázku zelenou farbou. Jej priložením sme pokryli práve jedno políčko v každom štvorci \(2\times 2\), ktorý neobsahoval odtok. A teda nám ostali štyri štvorce \(2\times 2\), z ktorých každý má práve jedno pokryté a tri nepokryté políčka.

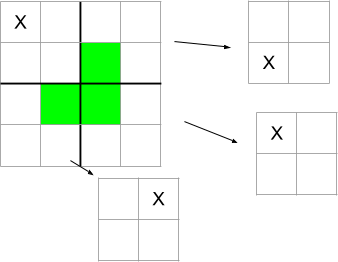
Teraz uvažujme mriežku \(4\times 4\), ktorá má odtok niekde inde. Zjavne aj tú vieme celú pokryť, a to presne rovnakým postupom. Jediný rozdiel bude v tom, že bude inak otočená kachlička v tom štvorci \(2\times 2\), ktorý obsahuje odtok.

Ako je to s väčšími mriežkami? Mriežku \(8\times 8\) si môžeme rozdeliť na štyri mriežky rozmerov \(4\times 4\). Je jasné, že iba v jednom z týchto blokov je práve jedno políčko zabrané odtokom. Vhodným uložením jednej “zelenej” kachličky ku stredu mriežky teraz vieme zabrať po jednom políčku aj v každom zo zvyšných troch blokov. No a každý z týchto blokov vieme vyriešiť vyššie popísaným spôsobom.

No a tento postup už ľahko zovšeobecníme: ľubovoľnú mriežku veľkosti \(2^k\times 2^k\) vieme rozdeliť na štyri mriežky veľkosti \(2^{k-1}\times 2^{k-1}\) a následne vieme vhodne priložiť jednu kachličku tak, aby každá mriežka menších rozmerov mala jedno políčko, ktoré už netreba pokryť. Potom sa na každú z menších mriežok rekurzívne zavoláme, čiže pre každú z nich znova zopakujeme túto istú úvahu.

Vhodnou implementáciou tohto riešenia je jedna rekurzívna funkcia, ktorá si bude pamätať, akú časť mriežky vypĺňa a kde v nej sa nachádza “odtok”, teda to jedno políčko, ktoré je už pokryté. Pamäťová zložitosť tohto riešenia je \(O(n^2)\), kedže si pamätáme iba mriežku, do ktorej zároveň hneď dopĺňame kachličky.

Časová zložitosť je tiež \(O(n^2)\), čiže priamo úmerná veľkosti mriežky. Prečo? Pri každom zavolaní našej funkcie totiž spravíme konštantne veľa výpočtov a priložíme jednu kachličku. No a keďže kachličiek je \((n^2-1)/3\), toľko bude aj volaní našej funkcie.

#include <iostream>
#include <vector>

using namespace std;

// mame 4 rozne natocenia kachlicky
// X1 2X 33 44
// 11 22 X3 4X

const vector<int> dx = {0, 0, -1, -1};
const vector<int> dy = {0, -1, 0, -1};

vector<pair<int, int> > d2 = { {0, 0}, {-1, 0}, {0, 1} };
vector<pair<int, int> > d4 = { {0, 0}, {0, 1}, {1, 0} };
vector<pair<int, int> > d3 = { {0, 0}, {1, 0}, {0, -1} };
vector<pair<int, int> > d1 = { {0, 0}, {0, -1}, {-1, 0} };

vector<vector<pair<int, int> > > delta = {d1, d2, d3, d4};

int kvadrant(const int i, const int j, const int pol_size, const int a, const int b)
// v ktorom kvadrante sa (a;b) nachadza :
// 1 2
// 3 4
{
    int counter = 1;
    
    for(int k=0;k<2;++k)
        for(int l=0;l<2;++l)
        {
            int roh_i = i + k*pol_size;
            int roh_j = j + l*pol_size;
            
            if(a >= roh_i && a < roh_i + pol_size && b >= roh_j && b < roh_j + pol_size) return counter;
            
            ++counter;
        }
        
    return -1;
}

int ozn = 1;

void zapis(vector<vector<int> >& vypln, const int i, const int j, int typ)
// vypln kachlicku so stredom v i;j otocenia typ
{
    for(int k=0;k<3; ++k) vypln[i+delta[typ-1][k].first][j+delta[typ-1][k].second] = ozn;
    ++ozn;
}

void f(vector<vector<int> >& vypln, const int a, const int b, const int i, const int j, const int size)
// rekurzivna funkcia vlozi do 3 spravnych kvadrantov jednu kachlicku
{
    if(size == 1) return;
    
    int size_new = (size)/2;
    int kde = kvadrant(i, j, size_new, a, b);
    
    zapis(vypln, i+size_new+dx[kde-1], j+size_new+dy[kde-1], kde);
    
    int counter = 1;
    for(int k=0;k<2;++k)
            for(int l=0;l<2;++l, ++counter)
            {
                if(kde == counter)
                {
                    f(vypln, a, b, i+k*size_new, j+l*size_new, size_new); 
                    continue;
                }
                
                f(vypln, i+size_new-1+k*1, j+size_new-1+l*1, i+k*size_new, j+l*size_new, size_new);
            }
    
    return;
}

int main()
{
    int n, a, b;
    cin >> n >> a >> b;
    --a, --b;
    
    vector<vector<int> > vypln(n, vector<int>(n, 0));
    vypln[a][b] = -1;
    
    f(vypln, a, b, 0, 0, n);
    
    for(int i=0;i<n;++i)
    {
        for(int j=0;j<n;++j)
        {
            if(j != 0) cout << " ";
            
            if(vypln[i][j] == -1) cout << 'X';
            else cout << vypln[i][j];
        }
        cout << "\n";
    }
    
    return 0;
}