1. Trefa do čierneho vzorové riešenie

Zadanie

Rozpálené slnko už pár dní pieklo, a tak sa Emo so Samom rozhodli, že sa uchýlia do klimatizovanej haly a zahrajú si partičku squashu. Emo využíval všetky svoje tenisové schopnosti. Keď raz napriahol ruku a švihol raketou v snahe odbiť loptičku, trafil miesto nej Samovu nohu. Tak bol ich zápas predčasne ukončený a každý išiel späť svojou cestou.

Samo sa teraz potrebuje vrátiť na internát, ktorý sa nachádza od haly smerom presne na severovýchod. Najradšej by išiel najkratšou trasou – priamo na severovýchod. Keďže po zničujúcom údere jeho noha nie je úplne v poriadku, nie celkom sa mu to darí. Chvíľu poskakuje na svojej zdravej ľavej nohe, no vtedy namiesto toho, aby išiel na severovýchod, ide smerom na východ. Chvíľu potom kráča po oboch a vtedy sa mu darí kráčať na sever. Potom ho noha ale zase začne bolieť a musí poskakovať, a teda ísť na východ. Toto sa dookola opakuje a Samo teda miesto priamo na severovýchod ide cik-cak, raz na východ, raz na sever.

Keďže si Samo nie je istý, či sa takto vôbec dostane na internát, zaujímalo by ho, koľkokrát by pretol svoju ideálnu trasu (polpriamku idúcu od haly na severovýchod), ak by takýmto spôsobom pokračoval donekonečna.

Úloha

Samo sa na začiatku nachádza v bode \((0,0)\) súradnicovej sústavy. Jeho pohyb sa dá popísať pomocou dvoch čísel \(d_x\) a \(d_y\). Samo postupne donekonečna opakuje dva posuny:

• Posun o \(d_x\) metrov smerom na východ (v smere rastúcej \(x\)-ovej súradnice)
• Posun o \(d_y\) metrov smerom na sever (v smere rastúcej \(y\)-ovej súradnice)

Vašou úlohou je zistiť, koľkokrát takto pretne priamku \(x=y\), pričom za pretnutie rátame aj dotyk s priamkou.

Formát vstupu

Aby sme mohli presnejšie testovať rýchlosť vašich riešení, v každom testovacom vstupe bude potrebné vyriešiť úlohu pre viacero dvojíc \(d_x, d_y\).

Na prvom riadku vstupu bude číslo \(t ~ (1 \leq t \leq 1000)\), určujúce počet zadaní úlohy, ktoré treba vyriešiť. Nasleduje \(t\) riadkov, každý z nich obsahuje dve celé čísla \(d_x, d_y ~ (1 \leq d_x, d_y \leq 10^{15})\) oddelené medzerou: číslo \(d_x\) predstavujúce dĺžku posunu smerom na východ a číslo \(d_y\) predstavujúce dĺžku posunu smerom na sever.

Formát výstupu

Pre každú zadanú dvojicu \(d_x, d_y\) vypíšte do samostatného riadku počet pretnutí Samovej cesty s priamkou \(x=y\). V prípade, že priamku cesta pretne nekonečne veľa ráz, vypíšte \(-1\). Nezabudnite vypísať znak konca riadku aj za posledným riadkom výstupu.

Hodnotenie

Vaše riešenia budú testované na štyroch sadách testovacích vstupov, pre ktoré platí:

Sada	1	2	3	4
Maximálne \(d_x, d_y\)	\(1000\)	\(10^{6}\)	\(10^{12}\)	\(10^{15}\)

Všimnite si, že čísla \(d_x\) a \(d_y\) presiahnu \(2^{31} - 1\) (zhruba \(2\cdot 10^9\)), čo je najväčšie číslo, ktoré sa dá uložiť v \(32\)-bitovej premennej so znamienkom. Použite preto \(64\)-bitové premenné typu long long v C++ a Int64 v Pascale.

Príklad

Input:

2
1 1
3 2

Output:

-1
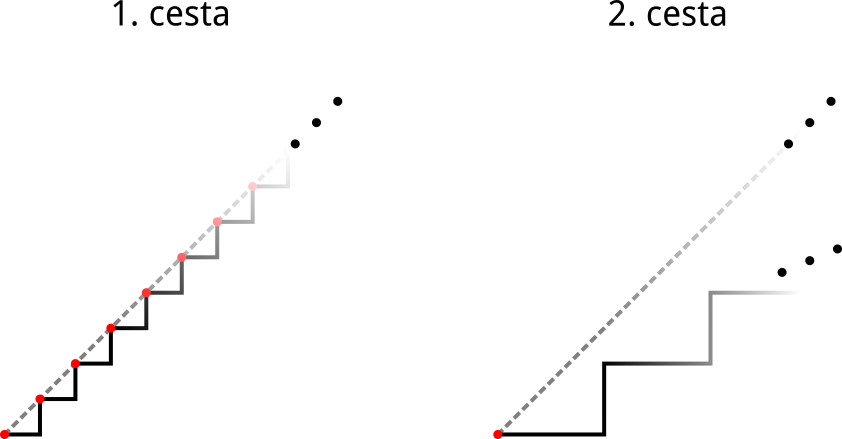
1

Pri prvej ceste sa Samo priamky dotkne nekonečne veľa ráz. Pri druhej ceste sa priamky dotkne iba v bode \((0, 0)\).

Hrubá sila

Pri tomto riešení budeme často potrebovať zistiť, či sme pod alebo nad priamkou \(y = x\). To je jednoduché: pod priamkou sa nachádzame, ak je súradnica \(x\) väčšia ako \(y\), v opačnom prípade sme nad priamkou.

Najjednoduchšie riešenie, ktoré by nám pri tejto úlohe mohlo napanúť, je postupné simulovanie Samových posunov a rátanie pretnutí s priamkou. Problém ale je, že takéto posuny by mohli trvať potenciálne donekonečna. Preto sa treba najprv zamyslieť, kedy môžeme so simuláciou prestať. Podľa toho, v akom vzťahu sú veľkosti posunov \(d_x\) a \(d_y\), môžu nastať nasledujúce prípady:

• \(d_x=d_y\): po každých 2 posunoch sa ocitneme opäť na priamke \(x=y\), teda dotykov s priamkou bude nekonečne veľa.
• \(d_x>d_y\): s priamkou sa stretneme iba raz, a to v bode \((0,0)\). Od nášho prvého pohybu sa už budeme stále nachádzať iba pod priamkou (rozmyslite si).
• \(d_x<d_y\): tu sa budeme s priamkou stretávať rôzne veľa krát. Stačí nám ale uvedomiť si, že ak sa pri nejakom pohybe doprava nepretneme s priamkou, už nikdy sa s ňou nepretneme. Od tohto momentu budeme totiž celý čas už iba nad priamkou.

Keď už poznáme tieto tri situácie, môžeme sa pustiť do programovania nášho riešenia. Na začiatku skontrolujeme, či sa veľkosti posunov nerovnajú, alebo či nie je posun doprava väčší ako ten smerom hore. Ak áno, vypíšeme potrebný výsledok. Ak nie, simulujeme pohyb po mriežke a po každom kroku zistíme, či sme sa pretli s priamkou. S priamkou sa pretneme vtedy, ak sme išli spod priamky nad ňu, alebo naopak (samozrejme, nezabúdame na ošetrenie dotyku s priamkou). Ak sme sa pri niektorom pohybe doprava nepretli s priamkou, simuláciu ukončíme a vypíšeme počet pretnutí.

Pamäťová zložitosť tohto riešenia je \(O(1)\), keďže miesto, kde sme, a veľkosti posunov si udržiavame v pár premenných.

Časová zložitosť riešenia je priamo úmerná počtu krokov, ktoré odsimulujeme. Ten je zhruba rovný počtu pretnutí s priamkou (ak dva kroky po sebe priamku nepretneme, simuláciu ukončíme). Ako si ukážeme v časti o ideálnom riešení, počet pretnutí je (v zaujímavom prípade \(d_x < d_y\)) zhruba \(d_x/(d_y-d_x)\), časová zložitosť je preto \(O(d_x/(d_y-d_x))\) = \(O(d_x)\).

#include <iostream>
using namespace std;

int main() {
  int t;
  cin >> t;
  for (int i = 0; i < t; i++) {
    long long dx, dy;
    cin >> dx >> dy;
    if (dx == dy) {
      cout << -1 << endl;
      continue;
    }
    if (dx > dy) {
      cout << 1 << endl;
      continue;
    }
    long long somx = 0, somy = 0, pocet = 0;
    while (true) {
      if (somx == somy) pocet ++;
      if (somx < somy && somx + dx > somy) pocet ++;
      somx += dx;
      if (somx < somy) break;
      if (somx == somy) pocet ++;
      if (somy < somx && somy + dy > somx) pocet ++;
      somy += dy;
    }
    cout << pocet << endl;
  }
}

Ideálne riešenie

Ako sme si pri riešení hrubou silou mohli všimnúť, v dvoch prípadoch sme mali odpoveď hneď, bez akejkoľvek simulácie. Ak sa bližšie zamyslíme a nakreslíme si pár obrázkov, zistíme, že aj v poslednom prípade vieme počet dotykov vypočítať v konštantnom čase.

Simuláciu sme ukončovali, keď sme prvý raz urobili krok doprava, pri ktorom sme našu priamku nepretli, ale zostali sme nad ňou. Bol to vlastne prvý krok doprava, po ktorom bola naša \(y\)-ová súradnica väčšia, než \(x\)-ová. Pozrime sa preto na body, v ktorých budeme po pohybe smerom vpravo, čiže po prvom kroku, po treťom kroku, atď. a všímajme si, o koľko je ich \(x\)-ová súradnica väčšia, než \(y\)-ová. Po prvom posune má \(x\)-ová súradnica “náskok” \(d_x\), keďže sme v bode \((d_x, 0)\). Po každých dvoch krokoch však \(y\)-ová súradnica tento “náskok” stiahne o \(d_y - d_x\). Na to, aby \(y\)-ová súradnica “dobehla” tú \(x\)-ovú, teda treba \(\lceil d_x/(d_y-d_x) \rceil\) takýchto dvojkrokov. Pri každom takomto dvojkroku, možno s výnimkou posledného, pretneme priamku dvakrát, počet pretnutí teda bude zhruba \(2 d_x/(d_y-d_x)\).

Do vzorca nesmieme zabudnúť pripočítať pretnutie v bode \((0,0)\) kde začíname. Ďalej je potrebné si uvedomiť, že nám vzniknú 2 prípady, pri ktorých sa počty mierne líšia:

• V prípade, že je \(d_x\) deliteľné číslom \(d_y-d_x\), po \(d_x / (d_y-d_x)\) dvojkrokoch budeme presne na priamke. To znamená, že v každom dvojkroku priamku pretneme dvakrát, spolu s pretnutím v bode \((0, 0)\) teda dostávame vzorec: \(2 \cdot d_x/(d_y-d_x) + 1\)

• Ak \(d_x\) nie je deliteľné číslom \(d_y - d_x\), po \(\lceil d_x / (d_y-d_x) \rceil\) dvojkrokoch skončíme nad priamkou. To znamená, že v poslednom z týchto dvojkrokov sme priamku pretli iba raz. Spolu s pretnutím v \((0,0)\) teda dostaneme vzorec: \(2 \cdot \lceil d_x/(d_y-d_x) \rceil\).

Časová aj pamäťová zložitosť tohto riešenia je konštantná, keďže potrebujeme iba pár premenných na výpočet vzorca, teda \(O(1)\).

Technická poznámka

Pri výpočte hodnoty \(\lceil d_x/(d_y-d_x) \rceil\) potrebujeme vydeliť dve čísla a výsledok zaokrúhliť nahor. Programovacie jazyky ako Python a C++ však pri celočíselnom delení zaokrúhľujú nadol. Preto v kóde vzorového riešenia využívame fakt, že \(d_x\) nie je deliteľné číslom \(d_y - d_x\), teda \(\lceil d_x/(d_y-d_x) \rceil = \lfloor d_x / (d_y - d_x) \rfloor + 1\).

#include <iostream>
using namespace std;

int main() {
  long long t;
  cin >> t;
  long long dx, dy;
  for (int i = 0; i < t; i++) {
    cin >> dx >> dy;
    if (dx == dy) {
      cout << -1 << endl;
      continue;
    }
    if (dx > dy) {
      cout << 1 << endl;
      continue;
    }
    if (dx % (dy - dx) != 0)
      cout << 2 * (dx / (dy - dx)) + 2 << endl;
    else
      cout << 2 * (dx / (dy - dx)) + 1 << endl;
  }
}

t = int(input())
for testcase in range(t):
    dx, dy = map(int, input().split())
    if dx == dy:
        print(-1)
    elif dx > dy:
        print(1)
    else:
        if dx % (dy - dx) == 0:
            print(dx // (dy - dx) * 2 + 1)
        else:
            print(dx // (dy - dx) * 2 + 2)