3. Hurá na Oravu vzorové riešenie

Zadanie

Andrej trávil túto ukrutnú zimu na chate v lyžiarskom stredisku na Orave. Ako každý správny lyžiar. Jedného dňa našiel na samom spodku strediska billboard s reklamou na najlepšiu pečenú klobásku na Orave. Bufet s klobásou sa mal nachádzať pri jednej z mnohých staníc lanovky, ktoré sa v stredisku nachádzali. Informácie na billboarde tiež obsahovali šifrovanú mapu popisujúcu cestu k bufetu.

Mapa k bufetu sa skladala iba z písmen L a P. Lyžiarske stredisko, v ktorom sa lyžoval, totiž vyzeralo nasledovne. Na samom spodku, teda tam kde stál Andrej, bola stanica lanovky s číslom 1. Tou sa mohol vyviezť buď na vrch ľavého alebo pravého svahu. Každý z týchto svahov mal na vrchole ďalšiu stanicu lanovky, z ktorej sa opäť dalo vyviezť na vrch ľavého alebo pravého svahu, na ktorých vrcholoch boli ďalšie stanice s lanovkami vedúcimi doľava a doprava…

Každá stanica lanovky bola naviac označená jedným číslom a pre tieto čísla platila nasledovná vlastnosť. Keď sa človek vyviezol ľavou lanovkou, dostal sa do stanice s číslom dvakrát väčším ako bolo číslo stanice, z ktorej vychádzal. A ak si vybral pravú lanovku, toto číslo bolo o jedna väčšie ako dvojnásobok východzej stanice. Ako správny gurmán (a lyžiar) si Andrej povedal, že musí zistiť, či billboard vraví pravdu a vydal sa na cestu za klobáskou.

Prešlo niekoľko dní a Andrej sa stále nevracal. Jeho rodina teda horskej službe nahlásila, že sa stratil cestou za najlepšou klobáskou Oravy. To bol pre záchranárov dostatočný záchytný bod a ponáhľali sa k billboardu s mapou, aby zistili, pri ktorej stanici lanovky by Andrej mohol byť. Nanešťastie, billboard bol poškodený a niektoré písmená mapy boli nečitateľné. Zúfalí záchranári teraz potrebujú vašu pomoc. Pri ktorých staniciach sa môže nachádzať bufet s klobáskou a snáď aj Andrej?

Úloha

Vašou úlohou je napísať program, ktorý na výstup vypíše súčet všetkých čísel staníc lanovky, pri ktorých môže byť bufet s klobáskou. K dispozicii máte mapu skladajúcu sa zo znakov L, P a *. Znak * reprezentuje poškodené miesta na mape, na ktorých mohol byť pôvodne ľubovoľný zo znakov L a P. Táto mapa popisuje cestu k bufetu začínajúcu pri stanici číslo 1.

Mapa sa číta zľava doprava. Ak sa nachádzame na stanici s číslom \(k\), tak pri písmene L sa musíme posunúť doľava do stanice \(2k\) a pri písmene P doprava do stanice \(2k + 1\). Pri znaku * musíme počítať s obomai možnosťami – stanicami \(2k\) aj \(2k+1\).

Formát vstupu

Vstup tvorí jediný riadok obsahujúci postupnosť znakov L, P a *, ktorá popisuje mapu ku klobáske. Táto postupnosť bude mať dĺžku najviac \(10^5\).

Formát výstupu

Na výstup vypíšte jedno číslo – súčet všetkých čísel staníc lanovky, pri ktorých sa môže nachádzať bufet. Keďže toto číslo môže byť pomerne veľké, vypíšte iba jeho zvyšok po delení \(1\,000\,000\,007\).

Príklady

Input:

P*L*

Output:

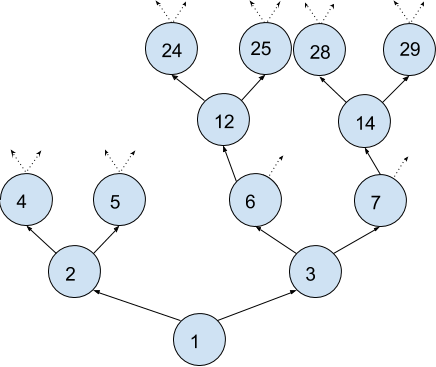
106

Mapa popisuje cestu od stanice číslo \(1\). V prvom kroku musíme ísť doprava (znak P), teda do stanice \(3\). Následne nevieme, ktorým smerom ísť, môžeme preto ísť buď do stanice \(6\) alebo \(7\). Ďalší krok vedie doľava, teda sa môžeme ocitnúť buď pri stanici \(12\) (naľavo od \(6\)) alebo \(14\) (naľavo od \(7\)). Nakoniec opäť nevieme, ktorým smerom ísť, takže bufet môže byť pri ľubovoľnej zo staníc \(24\), \(25\), \(28\) alebo \(29\). Hľadaný súčet je preto \(24 + 25 + 28 + 29 = 106\).

Input:

**

Output:

22

Našou úlohou bolo nájsť súčet čísel všetkých staníc, na ktorých mohol Andrej skončiť, ak sa riadil pokynmi na mape, na ktorej boli pôvodne iba dva typy pohybu – vľavo a vpravo. Vypočítať číslo novej stanice bolo pritom veľmi jednoduché. Ak Andrej stál pri stanici s číslom \(k\) a pohol sa doľava, dostal sa do stanice \(2k\), ak išiel doprava, tak do stanice \(2k +1\). V úlohe bol však jeden zádrheľ. Keďže niektoré pokyny na mape boli nečitateľné (*), museli sme pri nich brať do úvahy obe možnosti.

Simulácia

Na začiatok môžeme skúsiť odsimulovať Andrejov pohyb po lyžiarskom stredisku. Pokyny z mapy budeme spracovávať jeden po druhom a celý čas si budeme pamätať čísla všetkých staníc, na ktorých sa Andrej mohol nachádzať. Na začiatku bol Andrej v stanici číslo 1.

Pokyny sa spracovávajú jednoducho. Ak je na mape L, tak prejdeme cez všetky čísla a vynásobíme ich 2, pri P k nim okrem zdvojnásobenia pripočítame 1. Jediný problém je znak *, pri ktorom z každej stanice vedú dve možnosti. Preto si zapamätáme obe z nich, ak bol Andrej v stanici \(k\) tak po znaku * mohol byť aj v stanici \(2k\) aj v \(2k + 1\). Po spracovaní všetkých znakov z mapy jednoducho spočítame výsledné čísla staníc, čím dostaneme hľadanú odpoveď.

Problémom je však pamäťová a časová zložitosť. Pri každom znaku * zdvojnásobujeme počet čísel, ktoré si musíme pamätať. Preto ak by na mape boli samé *, čo sa stať môže, tak pamäťová aj časová zložitosť je \(O(2^n)\).

#include <iostream>
#include <vector>
using namespace std;

const int MOD = 1000000007;

int main() {
    char vstup;
    vector<long long> stanice = {1};    // pociatocna stanica 
    while(cin >> vstup) {
        if(vstup == 'L') {
            for(int i = 0; i < stanice.size(); i++) {
                stanice[i] = (2 * stanice[i]) % MOD;
            }
        }
        else if(vstup == 'P') {
            for(int i = 0; i < stanice.size(); i++) {
                stanice[i] = (2 * stanice[i] + 1) % MOD;
            }
        }
        else {
            int size = (int)stanice.size();    // vo for cykle menim velkost pola stanice, preto nemozem pouzit .size()
            for(int i = 0; i < size; i++) {
                stanice[i] = (2 * stanice[i]) % MOD;
                stanice.push_back((stanice[i] + 1) % MOD);
                }
        }
    }
    long long int vysledok = 0;
    for(int i = 0; i < stanice.size(); i++) {
        vysledok = (vysledok + stanice[i]) % MOD;
    }
    cout << vysledok << "\n";
}

Optimalizácia

Keď sa snažíme zlepšiť nejaké riešenie, vždy sa oplatí zamyslieť sa nad tým, či nerobíme niečo zbytočne. Hľadaným výsledkom je súčet všetkých staníc, kde sa Andrej môže nachádzať. Nepotrebujeme však vedieť, ktoré konkrétne stanice to sú. Možno si ich teda nemusíme pamätať.

Predstavme si, že Andrej môže byť v staniciach s číslami \(p\), \(q\), \(r\) a \(s\). Ak pôjde doľava (L), tak bude môcť byť v staniciach \(2p\), \(2q\), \(2r\) a \(2s\), ktorých súčet je dvakrát väčší ako súčet predchádzajúcich čísel. Ak si teda budeme pamätať iba jediné číslo – súčet všetkých možných staníc – tak ho pri znaku L vieme ľahko upraviť.

Pri znaku P majú nové stanice súčet \[(2p + 1) + (2q + 1) + (2r + 1) + (2s + 1) = 2(p+q+r+s) + 4\] Súčet sa opäť zdvojnásobil, naviac sa k nemu ale pripočítal počet staníc, v ktorých Andrej mohol byť. Vidíme, že pamätať si iba súčet nestačí, musíme si k nemu zapamätať aj počet staníc, v ktorých Andrej môže byť. Pomocou týchto dvoch čísel už vieme spracovať aj znak P.

Ostal nám znak *. Pri ňom by bol súčet nových staníc \[2p + 2q + 2r + 2s + (2p+1) + (2q+1) + (2r+1) + (2s+1) = 4(p + q + r + s) + 4\] Súčet sa teda zoštvornásobil a naviac sa k nemu pripočítal počet staníc. To však nie je problém pomocou našich dvoch hodnôt vypočítať. Vieme preto rýchlo spracovať aj znak *. Pri ňom však nemôžeme zabudnúť, že počet staníc, v ktorých Andrej môže byť, sa zdvojnásobí.

Naše riešenie teda opäť spracováva mapu znak po znaku, tentokrát si však pamätá iba dve hodnoty – súčet a počet staníc, v ktorých sa Andrej môže nachádzať. Ukázali sme si, že pri každom znaku vieme tieto dve čísla jednoduchým spôsobom upraviť na novú hodnotu. A aby sme nepracovali s príliš veľkými číslami, tak ich po každej operácii modulujeme číslom \(1\,000\,000\,007\).

Pamäťová zložitosť našeho riešenia bude konštantná (\(O(1)\)), pretože si pamätáme iba dve premenné. Časová bude lineárna od dĺžky mapy, teda \(O(n)\), pretože každý znak vieme spracovať v konštantnom čase úpravou najviac dvoch čísel.

#include <iostream>
using namespace std;

const int MOD = 1000000007;

int main() {
    char vstup;
    long long int sucet = 1, pocet = 1;
    while(cin >> vstup) {
        if(vstup == 'L') {
            sucet = (2 * sucet) % MOD;
        }
        else if(vstup == 'P') {
            sucet = (2 * sucet + pocet) % MOD;
        }
        else {
            sucet = (4 * sucet + pocet) % MOD;
            pocet = (2 * pocet) % MOD;
        }
    }
    cout << sucet << "\n";
}