Zadanie
V jeden zimný deň si Buj povedal, že bude lenivé prasa. Namiesto toho, aby šiel poctivo do školy, vybral sa do supermarketu, nakúpil neskutočne veľa čokolády, a potom ju zvyšok dňa konzumoval.
V ten deň zadal pán profesor algebry domácu úlohu. Buj sa o nej síce dozvedel z internetovej stránky predmetu, ale keďže na hodine nebol, netuší, ako ju má riešiť. Pomôžte mu!
Úloha
V tejto úlohe budeme pracovať s kompletne uzátvorkovanými výrazmi. Tie si definujeme takto:
- Reťazec \(a\) (jedno konkrétne písmeno a) je kompletne uzátvorkovaný výraz.
- Ak \(A\) a \(B\) sú kompletne uzátvorkované výrazy, tak aj \((A + B)\) je kompletne uzátvorkovaný výraz.
- Nič, čo sa nedá vyskladať postupným použitím dvoch predchádzajúcich pravidiel, nie je kompletne uzátvorkovaný výraz.
Podľa tejto definície sú kompletne uzátvorkované výrazy napríklad \(a\), \((a+a)\), \(((a+a)+a)\) a \((((a + a) + (a + a)) + ((a + a) + (a + a)))\). Vonkajšie zátvorky vo výrazoch vynechávame. Napríklad, namiesto \((a+(a+a))\) píšeme \(a+(a+a)\).
Na vstupe dostanete dva kompletne uzátvorkované výrazy. O nich chceme dokázať, že sa rovnajú. Môžeme pritom použiť iba asociatívny zákon, ktorý hovorí, že \(A+(B+C) = (A+B)+C\). V podstate teda chceme previesť prvý výraz na druhý, pričom sú povolené len dve operácie:
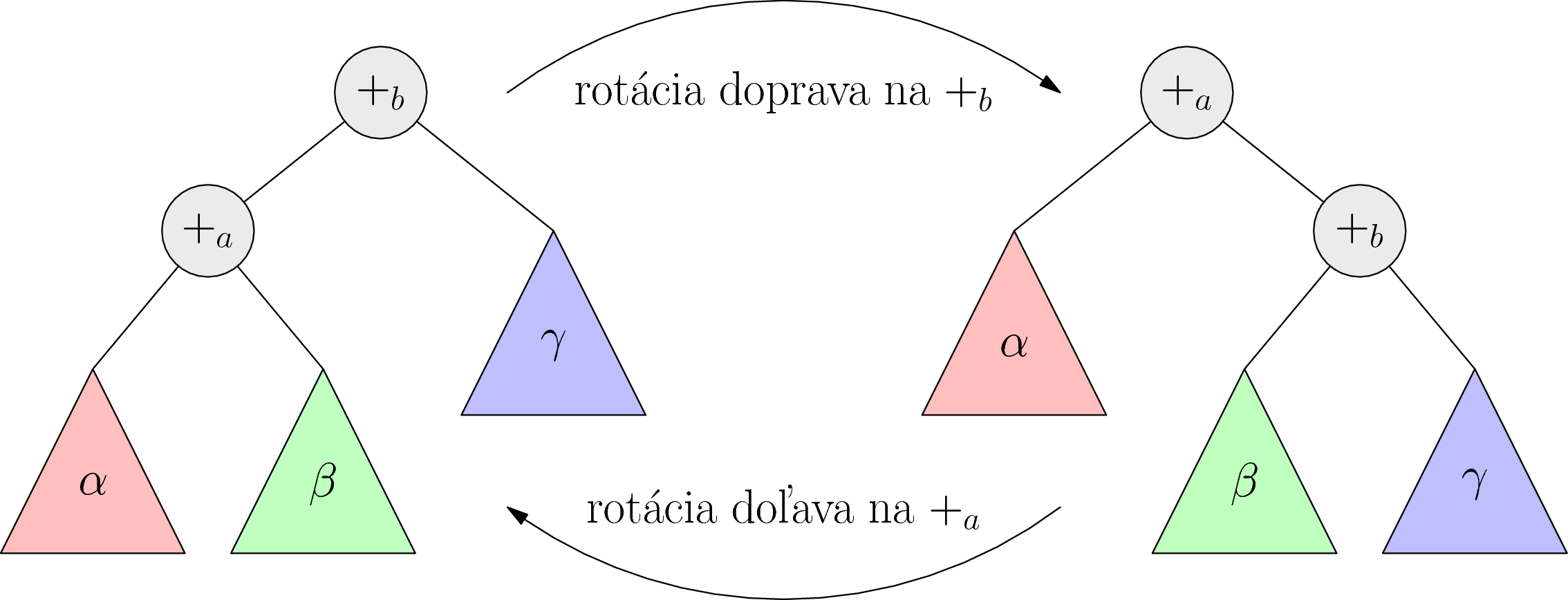
Ak v našom výraze máme podvýraz tvaru \((A+B)+C\), tak ho môžeme prepísať na \(A+(B+C)\). Napríklad výraz \[a + ((\, \overbrace{(a + a)}^{A} + \overbrace{\vphantom{(}a}^{B}) + \overbrace{(a + a)}^{C}\,)\] môžeme prepísať na \[a + (\, \overbrace{(a + a)}^{A} + (\overbrace{\vphantom{(}a}^{B} + \overbrace{(a + a)}^{C}\,)) \text{.}\] Tejto operácii budeme hovoriť rotácia doprava.
Prepísaniu opačným smerom, teda nahradenie podvýrazu tvaru \(A+(B+C)\) výrazom \((A+B)+C\), budeme hovoriť rotácia doľava.
Vašou úlohou je nájsť postupnosť rotácii, ktorou prevedieme prvý výraz na druhý.
Formát vstupu
Na prvom riadku vstupu je kladné číslo \(t\): počet testov. Nasledujú popisy jednotlivých testov. Každý test začína prázdnym riadkom, za ktorým nasledujú dva riadky obsahujúce jednotlivé výrazy. Môžete predpokladať, že oba výrazy majú rovnakú dĺžku, \(n\).
Je osem sád testovacích vstupov, obmedzenia pre jednotlivé sady sú nasledovné:
| Sada | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) | \(8\) |
|---|---|---|---|---|---|---|---|---|
| \(t \leq\) | \(1\,000\) | \(100\) | \(10\) | \(1\) | \(1\) | \(1\) | \(1\) | \(1\) |
| \(n \leq\) | \(40\) | \(120\) | \(400\) | \(1\,200\) | \(4\,000\) | \(12\,000\) | \(40\,000\) | \(400\,000\) |
Formát výstupu
Pre každý test vypíšte postupnosť rotácii, ktorou prevedieme prvý výraz na druhý, v nasledujúcom formáte. Na prvom riadku nech je dĺžka postupnosti, \(k\), a na nasledujúcich \(k\) riadkoch nech sú popisy jednotlivých rotácii v poradí, v akom ich vykonáme.
Očíslujme si znaky \(+\) v našom výraze zľava doprava \(1, 2, \ldots\), teda ak by sme z výrazu vynechali zátvorky, dostali by sme
\[a +_1 a +_2 a +_3 a +_4 \ldots\]
Rotáciu doprava z \((A +_i B) +_j C\) na \(A +_i (B +_j C)\) zapíšeme ako riadok “\(j\) R”. Podobne, rotáciu doľava z \(A +_i (B +_j C)\) zapíšeme ako “\(i\) L”.
Príklady
Input:
2
a+(a+(a+a))
((a+a)+a)+a
(a+a)+(a+a)
a+((a+a)+a)Output:
2
1 L
2 L
3
2 L
2 R
3 RPrvý postup: \[a+(a+(a+a))\ \rightarrow\ (a+a)+(a+a)\ \rightarrow\ ((a+a)+a)+a\] Druhý postup: \[(a+a)+(a+a)\ \rightarrow\ ((a+a)+a)+a\ \rightarrow\ (a+(a+a))+a\ \rightarrow\ a+((a+a)+a)\] Všimnite si, že druhý test sa dá vyriešiť aj na dve rotácie. Nám však stačí vypísať ľubovoľný funkčný postup.
Reprezentácia výrazu
S výrazom chceme vedieť robiť rotácie. Ak by sme ale pracovali s jeho textovou reprezentáciou, tak by sme zistili, že je to dosť nešikovné.
Zamyslime sa nad tým, čo to je kompletne uzátvorkovaný výraz. Je to buď \(a\), alebo \((A + B)\) pre nejaké kompletne uzátvorkované podvýrazy \(A, B\). Teda ak sme kompletne uzátvorkovaný výraz, musíme si pamätať, či sme prvého alebo druhého typu. A ak sme druhého typu, tak si musíme tiež pamätať ľavý podvýraz a pravý podvýraz. Z tejto úvahy vidno, že sa na výrazy dá pozerať ako na binárne stromy: koreň reprezentuje celý výraz, ľavý syn reprezentuje ľavý podvýraz a pravý syn reprezentuje pravý podvýraz.
Napríklad výrazu \((a + a) + (a + (a + a))\) prislúcha nasledujúci strom:
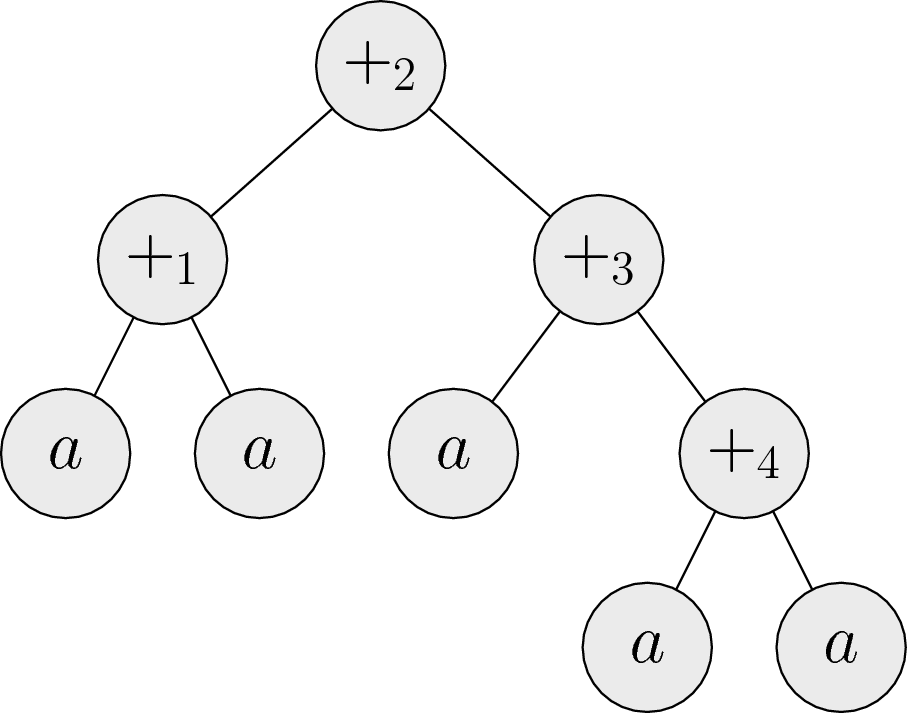
Na strome vieme rotáciu implementovať jednoducho: vrcholy pospájame hranami trochu iným spôsobom. Na obrázku nižšie ilustrujeme rotácie v oboch smeroch.
struct Vrchol {
int id = -1;
Vrchol* synovia[2] = {NULL, NULL}; // 0 lavy, 1 pravy
Vrchol* otec = NULL;
int smerKu(Vrchol* syn) {
// vrati smer k zadanemu synovi
if (synovia[0] == syn) return 0;
if (synovia[1] == syn) return 1;
}
bool jeList() {
return (synovia[0] == NULL) && (synovia[1] == NULL);
}
void nastavSyna(Vrchol* novy, bool smer) {
// uprav sebe linku na syna, a novemu synovi linku na otca
novy->otec = this;
synovia[smer] = novy;
}
void zrotuj(bool smer) {
// zrotuje okolo tohto vrcholu, 0 dolava, 1 doprava
Vrchol* povodnyOtec = otec;
Vrchol* novyOtec = synovia[!smer];
Vrchol* novySyn = novyOtec->synovia[smer];
nastavSyna(novySyn, !smer);
novyOtec->nastavSyna(this, smer);
if (povodnyOtec != NULL) {
povodnyOtec->nastavSyna(novyOtec, povodnyOtec->smerKu(this));
}
else {
novyOtec->otec = NULL;
}
}
};Ako ale z textovej reprezentácie dostaneme reprezentáciu stromovú? Tejto otázke je venovaná nasledujúca časť.
Parsovanie
Kedže ťažiskom úlohy nie je parsovanie, uvedieme tu iba rýchly algoritmus, ktorý nám z textovej reprezentácie vyrobí strom v čase \(O(n)\).
Myšlienka je taká, že budeme strom vyrábať od koreňa k listom, rekurzívne. Predstavme si, že nám zo vstupu postupne prichádzajú znaky výrazu, a my si chceme postupne vybudovať jeho strom. Máme niekoľko možností:
Buď je prvý znak výrazu
a, v takom prípade je náš výraz určite \(a\). Jemu prislúchajúci strom pozostáva iba z jedného vrcholu.Alebo je prvý znak
(. Potom je výraz je zložený, teda má tvar \((A + B)\) pre nejaké podvýrazy \(A\) a \(B\). Uvedomme si, že ďalej na vstupe dostaneme podvýraz \(A\), potom+, potom podvýraz \(B\) a nakoniec). Stačí nám preto rekurzívne vybudovať strom pre \(A\) (pričom ho celý prečítame), potom prečítame+, rekurzívne zostrojíme strom pre \(B\), a nakoniec prečítame). Stromy zavesíme pod spoločný koreň reprezentujúci prečítané+.
using namespace std;
Vrchol* parsuj(string& vyraz, int& pozicia, int& volneId) {
if (vyraz[pozicia] == 'a') { // podvyraz 'a'
pozicia++;
return new Vrchol;
}
// zostrojime stromy pre lavy a pravy operand
pozicia++; // precitame '('
Vrchol* lavy = parsuj(vyraz, pozicia, volneId);
int id = volneId;
volneId++;
pozicia++; // precitame '+'
Vrchol* pravy = parsuj(vyraz, pozicia, volneId);
pozicia++; // precitame ')'
// vyrob vrchol, ktoreho podstrom reprezentuje tento podvyraz
Vrchol* ja = new Vrchol;
ja->id = id;
ja->nastavSyna(lavy, 0);
ja->nastavSyna(pravy, 1);
return ja;
}
Vrchol* parsuj(string& vyraz) {
int pozicia = 0, volneId = 0;
return parsuj(vyraz, pozicia, volneId);
}Každý znak výrazu prečítame iba raz, preto je časová zložitosť algoritmu lineárna od dĺžky výrazu, teda \(O(n)\). Pamäťová zložitosť je \(O(n)\).
Rotovanie
Všetky naše algoritmy, pomalé či rýchle, budú založené na nasledovnom pozorovaní: keď na strom použijeme rotáciu, vhodnou rotáciou sa vieme vrátiť k pôvodnému stromu (viď obrázok vyššie).
Nemusíme teda priamo upravovať výraz \(A\) na \(B\), stačí nám oba výrazy upraviť na ten istý tvar \(C\) (tvar \(C\) budeme volať normálny tvar ). Na úpravu \(B\) na \(C\) sa potom pozrieme odzadu, čím dostaneme úpravu \(C\) na \(B\). Spolu s úpravou \(A\) na \(C\) nám to dokopy dá hľadanú úpravu \(A\) na \(B\).
Tvar \(C\) chceme z výrazov určit jednoznačne. Je prirodzené za tento normálny tvar zvoliť najľavejšie uzátvorkovanie výrazu, teda \(((((\ldots + a) + a) + a) + a)\). Tomu zodpovedá nasledovný strom:
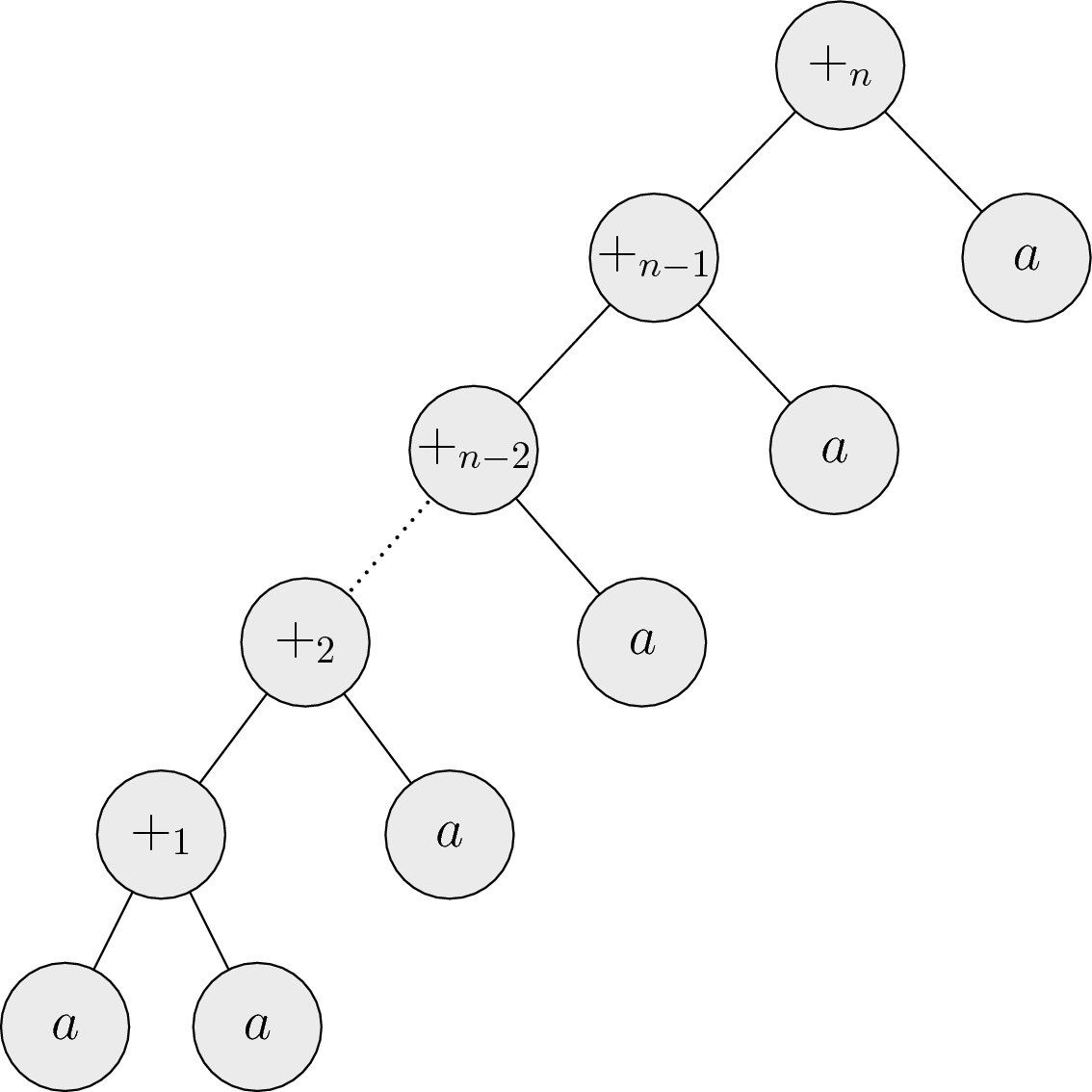
(Rovnako dobre by sme ale mohli použiť najpravejšie uzátvorkovanie, teda \((a + (a + (a + (a + \ldots))))\).)
Pomalé rotovanie
Chceme upraviť výraz \((A + B)\) na normálny tvar. Ťažko sa ale rozmýšľa nad prípadom, keď \(A\) a \(B\) môžu byť ľubovoľné. Ak by \(A\) a \(B\) mali nejaký konkrétny tvar, tak by sa nám s nimi možno ľahšie pracovalo. Už sa tu spomínali normálne tvary, ak by sme uvažovali tie, tak by sme mali navyše tú výhodu, že \(A\) a \(B\) by sme do nich vedeli dostať rekurzívne.
Predstavme si preto, že by \(A\) bol v najľavejšom uzátvorkovaní a \(B\) v najpravejšom. (Ako uvidíme, takáto voľba bude viesť k tomu, že veci budú vychádzať pekne.) Teda celý výraz vyzerá nasledovne:
\[(\overbrace{((((\ldots + a) + a) + a) + a)}^{l} +_l \overbrace{(a + (a + (a + (a + \ldots))))}^r)\]
kde \(l\) označuje počet \(a\)-čok v \(A\) a \(r\) označuje počet \(a\)-čok v \(B\). Čo sa s výrazom stane, ak by sme spravili rotáciu doľava na \(+\) spájajúcom \(A\) a \(B\)? Dostali by sme
\[(\overbrace{((((\ldots + a) + a) + a) + a)}^{l + 1} + \overbrace{(a + (a + (a + (a + \ldots))))}^{r - 1})\]
Teda vhodným počtom rotácii doľava vieme náš výraz dostať do najľavejšieho uzátvorkovania. Podobne vhodným počtom rotácii doprava vieme výraz dostať do najpravejšieho uzátvorkovania. Čo je presne to, čo chceme docieliť.
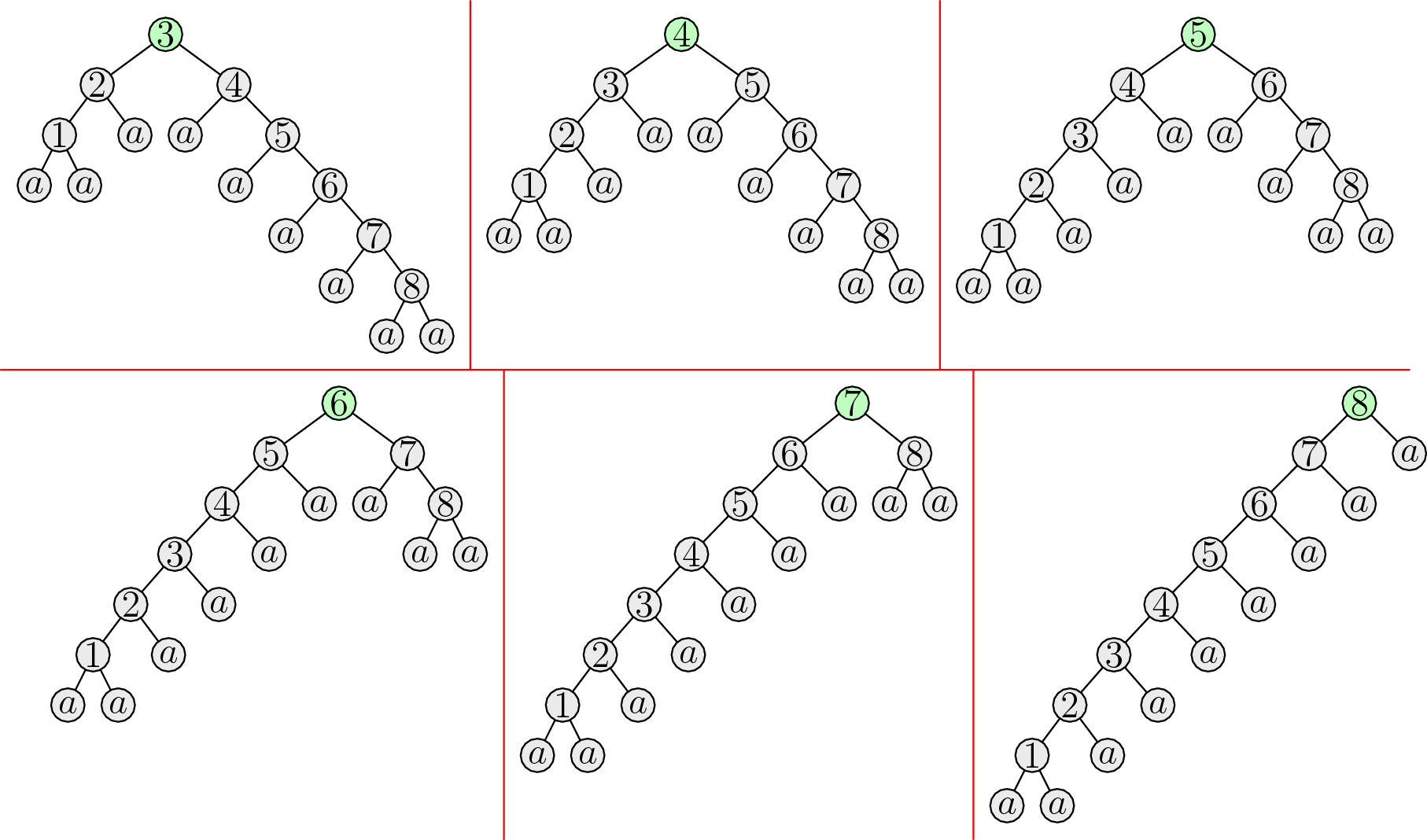
Predpokladali sme ale, že podvýraz \(A\) je v najľavejšom uzátvorkovaní a \(B\) v najpravejšom. To vo väčšine prípadov neplatí, čo s tým? Stačí ich na začiatku rekurzívne upraviť na požadovaný tvar.
#include <iostream>
#include <queue> // deque
#include "tree.cpp" // reprezentacia vyrazu
#include "parse.cpp" // parsovanie
using namespace std;
void doNormalnehoTvaru(Vrchol* koren, deque<pair<int, char> >& rotacie, bool inverz, bool smer) {
// Da strom do najlavejsieho/najpravejsieho uzatvorkovania (podla
// <smer>), a postupnost rotacii prida do <rotacie>. Ak
// <inverz> == true, tak tam prida namiesto toho inverznu postupnost.
if (koren->jeList()) {
return;
}
doNormalnehoTvaru(koren->synovia[0], rotacie, inverz, 0);
doNormalnehoTvaru(koren->synovia[1], rotacie, inverz, 1);
while (!koren->synovia[!smer]->jeList()) {
koren->zrotuj(smer);
if (inverz) {
rotacie.push_front({koren->otec->id, (smer ? 'L' : 'R')});
}
else {
rotacie.push_back({koren->id, (smer ? 'R' : 'L')});
}
koren = koren->otec;
}
}
void vyries(Vrchol* strom1, Vrchol* strom2, deque<pair<int, char> >& rotacie) {
// Do <rotacie> ulozi postupnost rotacii, ktora upravi <strom1>
// na <strom2>.
doNormalnehoTvaru(strom1, rotacie, false, 0);
deque<pair<int, char> > rotacie2;
doNormalnehoTvaru(strom2, rotacie2, true, 0);
for (int i = 0; i < (int)rotacie2.size(); i++) {
rotacie.push_back(rotacie2[i]);
}
}
void pridajVonkajsieZatvorky(string& vyraz) {
if ((int)vyraz.size() > 1) {
vyraz = '(' + vyraz + ')';
}
}
int main() {
int t;
cin >> t;
for (int test = 0; test < t; test++) {
// nacitame vyrazy a vyrobime stromove reprezentacie
string vyraz1, vyraz2;
cin >> vyraz1 >> vyraz2;
pridajVonkajsieZatvorky(vyraz1);
pridajVonkajsieZatvorky(vyraz2);
Vrchol* strom1 = parsuj(vyraz1);
Vrchol* strom2 = parsuj(vyraz2);
// vyriesime a vypiseme
deque<pair<int, char> > rotacie;
vyries(strom1, strom2, rotacie);
cout << rotacie.size() << "\n";
for (int i = 0; i < (int)rotacie.size(); i++) {
cout << rotacie[i].first + 1 << " " << rotacie[i].second << "\n";
}
}
return 0;
}Naša rekurzívna funkcia sa zavolá do každého vrcholu stromu práve raz, pričom v každom volaní urobíme nanajvýš \(O(n)\) roboty. To znamená, že určite nerobíme dokopy viac ako \(O(n^2)\) roboty. Ukazuje sa, že na najhorších vstupoch1 naozaj urobíme až kvadraticky veľa práce, teda časová zložitosť je \(\Theta(n^2)\). Pamäťová zložitosť je \(O(n)\), nakoľko pracujeme iba so stromom výrazu.
Rýchle rotovanie
Najprv algoritmus popíšeme a potom ukážeme, prečo je rýchly.
Ak má strom iba jeden vrchol, tak už je v najľavejšom uzátvorkovaní (reprezentuje výraz \(a\)). V opačnom prípade je koreň +, má ľavého aj pravého syna. Vtedy urobíme nasledovné:
Kým platí, že pravý syn koreňa nie je list (pravý podstrom koreňa obsahuje aspoň dva vrcholy), robíme rotácie doľava okolo aktuálneho koreňa. Pri každej takejto rotácii sa nám zmení koreň, pričom nový koreň bude mať pravý podstrom o niečo menší, než mal ten starý. Po konečnom počte krokov teda prídeme k stromu, kde je pravý syn koreňa list (zodpovedajúci výraz má tvar \((A + a)\)).
Ľavý podstrom koreňa rekurzívne upravíme na najľavejšie uzátvorkovanie.
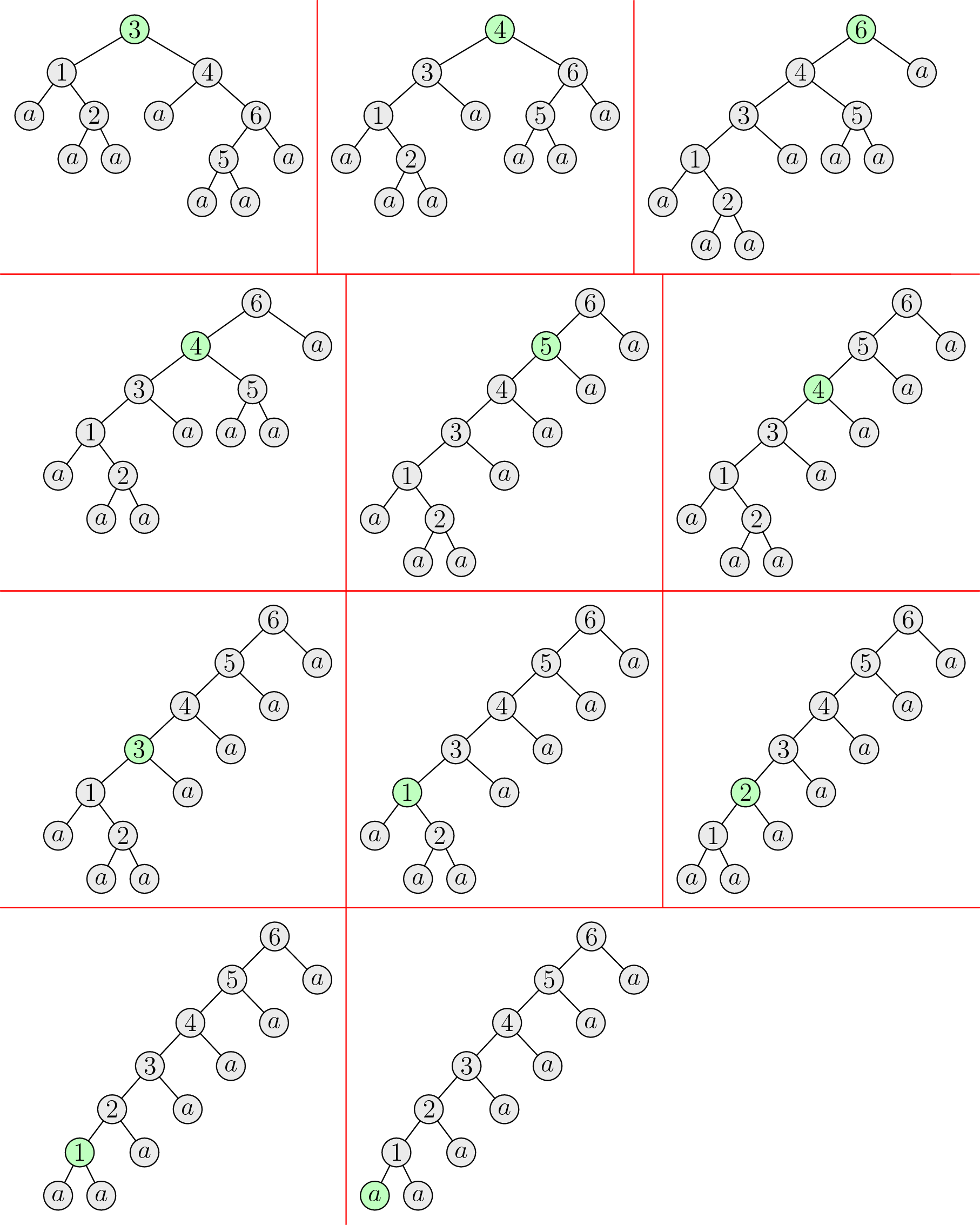
#include <iostream>
#include <queue> // deque
#include "tree.cpp" // reprezentacia vyrazu
#include "parse.cpp" // parsovanie
using namespace std;
void doLavehoTvaru(Vrchol* koren, deque<pair<int, char> >& rotacie, bool inverz) {
// Da strom do najlavejsieho uzatvorkovania, a postupnost rotacii
// prida do <rotacie>. Ak <inverz> == true, tak tam prida
// namiesto toho inverznu postupnost.
Vrchol* pivot = koren;
while (!pivot->jeList()) {
if (!pivot->synovia[1]->jeList()) {
pivot->zrotuj(0);
if (inverz) {
rotacie.push_front({pivot->otec->id, 'R'});
}
else {
rotacie.push_back({pivot->id, 'L'});
}
pivot = pivot->otec;
}
else {
pivot = pivot->synovia[0];
}
}
}
void vyries(Vrchol* strom1, Vrchol* strom2, deque<pair<int, char> >& rotacie) {
// Do <rotacie> ulozi postupnost rotacii, ktora upravi <strom1>
// na <strom2>.
doLavehoTvaru(strom1, rotacie, false);
deque<pair<int, char> > rotacie2;
doLavehoTvaru(strom2, rotacie2, true);
for (int i = 0; i < (int)rotacie2.size(); i++) {
rotacie.push_back(rotacie2[i]);
}
}
void pridajVonkajsieZatvorky(string& vyraz) {
if ((int)vyraz.size() > 1) {
vyraz = '(' + vyraz + ')';
}
}
int main() {
int t;
cin >> t;
for (int test = 0; test < t; test++) {
// nacitame vyrazy a vyrobime stromove reprezentacie
string vyraz1, vyraz2;
cin >> vyraz1 >> vyraz2;
pridajVonkajsieZatvorky(vyraz1);
pridajVonkajsieZatvorky(vyraz2);
Vrchol* strom1 = parsuj(vyraz1);
Vrchol* strom2 = parsuj(vyraz2);
// vyriesime a vypiseme
deque<pair<int, char> > rotacie;
vyries(strom1, strom2, rotacie);
cout << rotacie.size() << "\n";
for (int i = 0; i < (int)rotacie.size(); i++) {
cout << rotacie[i].first + 1 << " " << rotacie[i].second << "\n";
}
}
return 0;
}Prečo je tento algoritmus rýchly? Pozerajme sa v priebehu algoritmu na ľavú diagonálu – tak budeme volať množinu vrcholov, ktoré vieme dosiahnuť z koreňa tak, že sa niekoľkokrát presunieme po hrane do ľavého syna.
Vrchol, okolo ktorého rotujeme (teda koreň podstromu spracovávaného v aktuálnom volaní našej rekurzívnej funkcie), leží vždy na tejto diagonále. Pri každej rotácii sa počet vrcholov na tejto diagonále zväčší o \(1\) (rozmyslite si). Počet vrcholov na diagonále nemôže byť väčší, ako počet vrcholov stromu \(n\), teda spravíme nanajvýš \(n\) rotácii. Časová zložitosť je preto \(O(n)\). Pamäťová zložitosť je \(O(n)\).
Príklad zlého vstupu je “cik-cakový” strom, ktorý dostaneme z výrazu \((a + \dots ((a+((a+(a+a))+a))+a)) \dots + a))\).↩
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.