Zadanie
Ako tak študent Dávid cestou domov začal konzumovať čokoládu, jej úlomky dopadali na chodník. Na druhý deň išiel Dávid po tom istom chodníku, znova konzumujúc čokoládu a opäť mu zopár malých kúskov spadlo na zem. Táto situácia sa opakuje každý deň, lebo Dávid je svedomitý študent a zároveň veľký milovník čokolády.
Na začiatku tohto chodníka prebývajú mravce – bažiace po čokoláde, a mimochodom, mimoriadne expanzívne. Ak sa niekde v okolí mraveniska vyskytne kúsok čokolády, mravce neváhajú a rozšíria svoje mravenisko až po tento kúsok. Ak teda Dávid bude pokračovať vo svojom zvyku konzumovať čokoládu cestou zo školy, mravce časom skolonizujú celý chodník.
Dávid by ale nerád (nevedomky) predal našu krajinu mravcom. Keď od vás dostane každý deň údaj o tom, kde sa nachádza hranica mravčej ríše, uvedomí si vážnosť celej situácie a podnikne rázne protiopatrenia.
Úloha
Chodník má dĺžku \(n+1\) metrov. Môžeme si ho teda predstaviť ako časť číselnej osi od bodu \(0\) po bod \(n+1\). Zo začiatku je celé mravenisko v bode \(0\). Neskôr sa bude rozširovať na čoraz dlhší interval na chodníku.
Rozpínavosť mravcov sa dá charakterizovať kladným číslom \(v\) s nasledovným významom: ak sa niekedy vo vzdialenosti \(v\) alebo menej metrov od mraveniska nachádza kúsok čokolády, mravce ho pohltia a tak rozšíra svoje impérium až po tento kúsok. Ako pracovité tvory sú toto schopné urobiť v rámci jedného dňa ľubovoľne veľa ráz – posunutím hranice sa totiž môže stať, že mravce už ,,dočiahnu’’ aj na ďalšie kúsky čokolády, na ktoré predtým nedočiahli. Navyše, ak sa niekedy dostanú do vzdialenosti \(v\) alebo menej metrov od konca chodníka, rozšíria sa až po koniec chodníka (teda akoby na konci chodníka bola čokoláda).
Dávid má zvláštny talent na trúsenie čokolády. Po prvé, čokoládové omrvinky mu padajú iba na miesta, ktoré sú celočíselný počet metrov od začiatku chodníka. Okrem toho Dávidovi nikdy nepadne omrvinka dvakrát na to isté miesto. Zároveň však platí, že na všetky body \(1, 2, \dots, n\) mu časom nejaká omrvinka padne.
Kým sa mravce dostanú po koniec chodníka v bode \(n+1\), zopár dní im to potrvá. Vašou úlohou bude zistiť, kde sa bude nachádzať hranica mravčieho impéria po jednotlivých dňoch expanzie, až kým neskolonizujú celý chodník.
Formát vstupu
Na prvom riadku vstupu sa nachádzajú dve celé čísla \(n\) (\(2 \leq n \leq 100\,000\)) a \(v\) (\(1 \leq v \leq 100\,000\)) – počet omrviniek, ktoré Dávid vytrúsi, a expanzívnosť mravcov. Nasleduje \(n\) riadkov popisujúcich jednotlivé kúsky čokolády, ktoré Dávid vytrúsil. Každý z týchto riadkov obsahuje dve celé čísla \(m_i\) (\(1 \leq m_i \leq n\)) a \(d_i\) (\(0 \leq d_i \leq 100\,000\)) – pozíciu danej omrvinky a číslo dňa, keď táto omrvinka spadne. Dni číslujeme od nuly.
Môžete predpokladať nasledovné:
Kúsky čokolády budú na vstupe zoradené vzostupne podľa dňa, kedy padli. Viacero kúskov mohlo padnúť v rovnaký deň – na vstupe sa vtedy objaví skôr ten, ktorý padol na skorší meter chodníka.
Na každý meter chodníka medzi \(1\) a \(n\) (vrátane) padne práve jeden kúsok čokolády.
Keďže expanzívnosť mravcov je aspoň \(1\), určite sa časom dostanú až na koniec chodníka.
Riešenia, ktoré zvládnu riešiť iba prípady kde \(\boldsymbol{v = 1}\), získajú v praktickom testovaní približne polovicu bodov a môžu získať až polovicu bodov za popis.
Formát výstupu
Deň, počas ktorého sa mravce dostanú na koniec chodníka, označme \(c\). Vypíšte \(c+1\) čísel – na koľkom metri sa nachádzala hranica mraveniska na konci dňa \(0, 1, 2, 3, ..., c\). Každé číslo nech je na samostatnom riadku.
Príklady
Input:
6 1
1 2
3 2
5 2
2 3
4 4
6 4Output:
0
0
1
3
7V dňoch \(0\) a \(1\) nepadla žiadna čokoláda, mravce teda tieto dva dni ostanú na začiatku chodníka. Počas dňa \(2\) padne na meter \(1\) čokoláda, ktorú mravce pohltia. Hoci v ten istý deň padla omrvinka aj na metre \(3\) a \(5\), mravce ich nepohltia, pretože ich expanzívnosť je len \(1\). Počas dňa \(3\) padne čokoláda na meter \(2\) a vtedy mravce pohltia ďalšie \(2\) metre. Po ďalšom dni už budú schopné ovládnuť celý chodník.
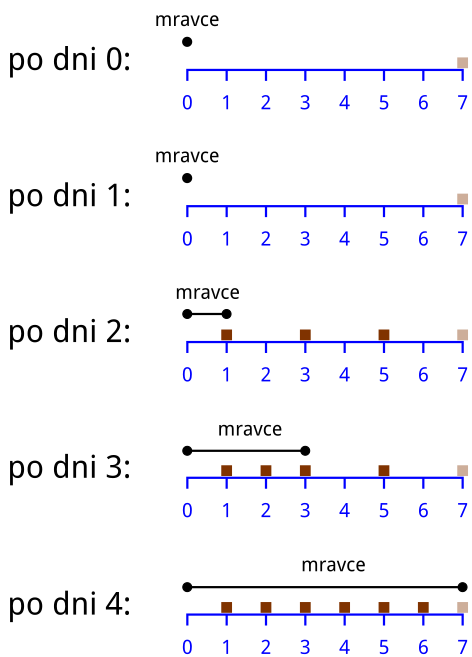
Input:
6 3
1 0
2 1
3 1
6 1
5 6
4 8Output:
1
7Na prvý meter padla čokoláda hneď, preto už od začiatku bude ríša hraničiť na prvom metri. Ďalší deň padne jedlo na metre \(2\), \(3\), \(6\). Kedže tieto body sú dostatočne blízko seba (aj bodu \(7\)), mravce rovno ovládnu všetko.
Povieme si najprv niečo o riešení za polovicu bodov (kde \(v = 1\)) a od neho sa dostaneme k vzorovému riešeniu.
Odporúčame vám si dôsledne preštudovať uvedené zdrojové kódy (keď budú zverejnené). Najmä riešitelia, ktorí ešte nie sú úplne zbehlí v programovaní, sa tak dozvedia veľa užitočných trikov. Každé riešenie obsahuje komentáre o tom, čo sa presne deje a prečo, netreba sa teda kódov báť.
Riešenie za polovicu bodov
Zo zadania sme museli najprv pochopiť, akým spôsobom sa mravčia ríša pohybuje pozdĺž chodníka. Toto správanie potom vieme jednoducho nasimulovať pomocou cyklov.
Do pamäte si uložíme pole reprezentujúce chodník, ktoré si nazveme chodnik[]. Na \(x\)–tej pozícii poľa bude uložené číslo dňa, v ktorom na \(x\)-tý meter chodníka dopadla omrvinka. Okrem poľa chodnik[] si budeme v našej simulácii pamätať aj číslo aktuálneho dňa (premenná den) a pozíciu, na ktorej končí mravčia ríša (premenná kde_som). Tieto premenné budú mať na začiatku hodnotu 0.
Algoritmus bude prebiehať nasledovne:
- Posúvame koniec mraveniska po chodníku ďalej pokiaľ platia obe nasledujúce podmienky:
- ešte sme nedosiahli koniec chodníka:
kde_som < n+1 - na ďalšom metri chodníka už je omrvinka:
chodnik[kde_som + 1] <= den
Pre posun na ďalší meter chodníka zväčšíme
kde_somo 1. - ešte sme nedosiahli koniec chodníka:
Keď sme sa dostali najďalej, ako to v daný deň išlo, inými slovami jedna z podmienok z kroku 1 prestala platiť, vypíšeme aktuálnu hodnotu
kde_soma zvýšime číslo dňa o 1. Po zvýšení hodnotydensa už možno budeme vedieť dostať po chodníku ďalej, kedže nám na chodníku možno pribudli ďalšie omrvinky. Ak sme sa ešte nedostali na koniec chodníka, znova pokračujeme krokom 1 a skúšame sa posunúť ďalej.
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int n, v;
cin >> n >> v;
// pole obsahujuce casy kedy padli omrvinky na chodnik
// chodnik[METER] = CISLO_DNA_KEDY_PADLA
vector<int> chodnik(n+1);
for(int i=0; i<n; i++)
{
int x, y;
cin >> x >> y;
chodnik[x]=y;
}
// premenne udrzujuce stav simulacie
int kde_som=0;
int den=0;
while (kde_som != n+1)
{
// Krok 1: posuvaj sa kym mozes
// teda, kym bud nedorazis na koniec chodnika
// alebo na dalsom metri chodnika este nepadla omrvinka
while (kde_som != n+1 && chodnik[kde_som+1]<=den)
kde_som++;
// Krok 2: kedze skoncil cyklus, uz sa dalej nevieme pohnut
// vypiseme vysledok, zvysime cislo dna.
cout << kde_som << endl;
den++;
// Nasleduje dalsia otacka cyklu (sme vo while cykle)
// Vyhodnoti sa podmienka, ci este nie sme na konci chodnika
}
}\({v > 1}\) – jednoduché, no trochu pomalé riešenie
Ak sme chceli získať na testovači aspoň 6 bodov, bolo sa treba popasovať aj so situáciami, kde je expanzívnosť mravcov väčšia než 1.
Ako sa takéto riešenie líši od toho predošlého? V kroku 1 našej simulácie sme schopnosť posunúť sa ďalej overovali podľa toho, či na nasledujúce políčko už dopadla omrvinka. Avšak mravce dokážu od svojej hranice dosiahnuť na \(v\) ďalších políčok, musíme preto urobiť takýchto kontrol \(v\) – jednu pre každé políčko, na ktoré dočiahnu. Všimnite si, že aj predtým sme ich potrebovali \(v\), akurát \(v\) bolo \(1\), a preto nám stačil jednoduchý if.
Na overenie druhej podmienky kroku 1 použijeme for cyklus, ktorý bude kontrolovať, či chodnik[kde_som + i] <= den pre všetky \(i\) od \(1\) po \(v\). Samozrejme, treba si dať pozor, aby sme sa takýmto skúšaním nepozerali za koniec chodníka.
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int n, v;
cin >> n >> v;
// pole obsahujuce casy kedy padli omrvinky na chodnik
// chodnik[METER] = CISLO_DNA_KEDY_PADLA
vector<int> chodnik(n+1);
for(int i=0; i<n; i++)
{
int x, y;
cin >> x >> y;
chodnik[x]=y;
}
// premenne udrzujuce stav simulacie
int kde_som=0;
int den=0;
// simulácia pre všetky dni
while (kde_som < n+1)
{
// urcuje, ci sa dokazem pohnut dalej
// a teda ma zmysel prehladavat nasledujucich V metrov chodnika
bool mozem = true;
// tento cyklus si nazvime Erik
// v rámci tohto dňa sa dostane tak ďaleko ako sa len dá
while (mozem)
{
mozem = false;
// idem prehladavat nasledujucich V policok
for (int i=1; i<=v; i++)
{
if ((kde_som+i) <= n+1 && chodnik[kde_som+i] <= den)
{
// ak som nasiel padnutu omrvinku niekde v dosahu,
// zapisem si, ze som ju nasiel, a potom budem moct z toho
// noveho miesta opat hladat, ci sa v nasledujucich V
// polickach nachadza dalsia omrvinka
mozem = true;
kde_som = kde_som+i;
// ak som nasiel, nemusim teraz hladat vo vsetkych V polickach
// a radsej rovno skoncim,
// kedze cyklus Erik v dalsej otacke spusti nove hladanie
// z tohto noveho miesta, ktore sme si predchvilou
// ulozili do kde_som
break;
}
}
}
cout << kde_som << endl;
den++;
}
return 0;
}Prečo sme za toto riešenie nedostali všetky body?
Samozrejme, takéto riešenie je pomalé. Zaujímavá otázka však je, prečo? Uvedomme si, čo sa v algoritme deje. Každý deň sa pozeráme na \(v\) nasledujúcich políčok a zisťujeme, či na niektoré z nich nepadla omrvinka. Hodnota \(v\) však môže byť veľká a mohlo sa nám stať, že všetky omrvinky padli v posledný možný deň. Poprípade omrvinky, ktoré padli ako prvé, padli na koniec chodníka.
Z toho vyplýva, že v najhoršom možnom prípade budeme musieť pre každý deň (počet dní označme \(max_{den}\)) naozaj skontrolovať \(v\) políčok a pri tom sa ani vôbec neposunúť. To vedie k zložitosti \(O(max_{den} \cdot v + N)\), čo je pre najväčšie možné hodnoty zo zadania priveľa.
Iný prístup
Namiesto toho, aby sme simulovali jednotlivé dni, poďme simulovať dopady jednotlivých omrviniek. Pomôže nám, že omrvikny sú na vstupe zoradené podľa času dopadu vzostupne – od prvej padnutej po poslednú.
Predstavme si, že stojíme na \(x\)-tom metri a na chodník dopadla ďalšia omrvinka. V závislosti od miesta jej dopadu vykonáme jednu z nasledovných akcií:
Ak dopadla do už obsadeného územia, čiže na meter menší alebo rovný \(x\), nemá zmysel niečo robiť. Mravce majú záujem expandovať len vpred, nie vzad.
Ak dopadla tak ďaleko, že na ňu práve nedočiahneme, nemá zmysel sa momentálne pokúšať expandovať. Do budúcna by sa nám ale táto informácia mohla zísť, preto si ju musíme niekam zapísať. Vytvoríme si pole
uz_padla[], do ktorého si na \(i\)-tu pozíciu zaznačíme, či už na \(i\)-ty meter chodníka padla omrvinka (uz_padla[i] = true). Poleuz_padla[]bude obsahovať hodnoty typuboolean, na začiatku sú všetkyfalse.Ak omrvinka dopadla pred nás, ale ešte stále v našom dosahu, budeme sa posúvať dopredu. Na rozdiel od predošlých riešení by sme však chceli každý meter chodníka skontrolovať najviac raz.
Ako sa múdro posúvať ?
Keď omrvinka padla niekam v rámci nášho dosahu, chceme sa k nej hneď posunúť. Ako však potom rýchlo nájsť ďalšiu omrvinku v dosahu? A ako to spraviť bez toho, aby sme zakaždým pýtali na tie isté políčka?
Na úplnom začiatku stojíme na metri 0 a vieme, že na chodník ešte nepadla žiadna omrvinka. Začneme omrvinky spracovávať v poradí, v akom sa objavili na vstupe, teda podľa času ich dopadu. Kým padajú ďalej ako je vzdialenosť \(v\), nevieme sa posunúť ďalej a iba si tieto omrvinky značíme do poľa uz_padla[].
Zmena nastane pri prvej omrvinke, ktorá dopadne na miesto \(x\), kde \(x \leq v\). V tom momente sa môžeme posunúť na pozíciu \(x\). Z novej pozície však možno dosiahneme na omrvinky, ktoré padli skôr. Mohli by sme sa preto začať pozerať na nasledujúcich \(v\) políčok a s pomocou poľa uz_padla[] zisťovať, či sa na nich nenachádza nejaká omrvinka. Pričom vždy keď nájdeme ďalšiu omrvinku v dosahu, tak sa posunieme na jej miesto
Uvedomme si však jednu dôležitú vec. Až po meter \(\boldsymbol{v}\) sa žiadna ďalšia omrvinka nenachádza. Na začiatku bol totiž chodník prázdny a omrvinka, ktorá padla na pozíciu \(x\) bola prvá omrvinka, ktorá padla do nášho dosahu. Nemusíme teda kontrolovať políčka \(x\) až \(v\), stačí nám skontrolovať pozície od \(\boldsymbol{v+1}\) po \(\boldsymbol{x+v}\).
Táto vlastnosť naviac platí aj vo všeobecnosti. Ak sme zastavili na metri \(y\), pričom sme sa nevedeli posunúť ďalej, bolo to preto, lebo sme skontrolovali všetky políčka po \(y+v\) a na žiadnom z nich sa omrvinka nenachádzala. Keď teda do nášho dosahu padne prvá omrvinka, stačí kontrolovať políčka začínajúc od pozície \(y+v+1\).
Toto zlepšenie spôsobí, že každý meter chodníka skontrolujeme najviac raz. Zakaždým totiž kontrolovanie začneme od poslednej skontrolovanej pozície. A keďže chodník má dĺžku \(n\), budeme potrebovať \(O(n)\) času.
Samozrejme, zadanie po nás chcelo, aby sme vypísali pozície, na ktorých stoja mravce v každý možný deň. To však vieme do nášho programu ľahko pridať. Ak totiž stojíme na metri \(x\), naposledy sme úspešne spracovali omrvinku, ktorá padla v deň \(d_1\) a ďalšia omrvinka padne až v deň \(d_2\) tak vieme, že odpoveď pre dni \(d_1\) až \(d_2-1\) bude \(x\).
Je si však treba uvedomiť, že veľkosť výstupu nesúvisí s hodnotou \(n\) a jeho vypísanie nám tiež zaberie čas úmerný počtu vypísaných čísel. Ak si teda posledný deň, keď padne nejaká omrvinka označíme \(max_{den}\), tak môžeme povedať, že časová zložitosť našeho algoritmu je \(O(n + max_{den})\). Pamäťová zložitosť bude \(O(n)\), keďže na naprogramovanie nám stačí jedno pole dĺžky \(n\).
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n, v;
cin >> n >> v;
// pole obsahujuce casy kedy padli omrvinky na chodnik
// chodnik[METER] = CISLO_DNA_KEDY_PADLA
vector<pair<int, int>> zrnka;
vector<bool> uz_padla(n+2, false);
uz_padla[n+1] = true;
// premenne ktore budeme potrebovat - kde som a v kolkom dni
// spomenute v kroku #1
int kde_som = 0;
int kam_kontroloval = 0;
int kolke_zrnko = 0;
for(int i=0; i<n; i++)
{
int meter, den;
cin >> meter >> den;
zrnka.push_back(make_pair(den, meter));
}
// pamatame si aj cislo dna, pretoze vzdy ked spracujeme niekolko zrniek,
// potrebujeme vypisat udaj, na akej pozicii sa prave nachadzame.
// - takze spracuvavaj zrnka az pokial dalsie zrnko uz nepatri
// do dalsieho dna. Cyklus JOZEF vtedy skonci, vypiseme vysledok pre dany den
// a zase spustime JOZEFa nech sa cykly pre zrnka z nasledujuceho dna
for (int den=0; kde_som < n+1; den++)
{
while (zrnka[kolke_zrnko].first == den) // cyklus JOZEF
{
int kam_padlo = zrnka[kolke_zrnko].second;
// dva krat s tym istym zrnkom robit nechceme!
kolke_zrnko++;
if (kam_padlo <= kde_som)
// pripad A - padlo niekam za nas - a teda nas nezaujima
continue;
else if (kam_padlo > kde_som + v)
{
// pripad B - padlo niekam za nas aktualny dosah
// zapiseme si to, bude nam to treba neskor
uz_padla[kam_padlo] = true;
continue;
}
else
{
// padlo niekam v nasom dosahu
// takze urcite sa chceme hned nanho presunut
kde_som = kam_padlo;
// vsimnite si tieto dve podmienky vo WHILE cykle
// vyhladavam len od miesta poslednej kontroly po aktualny dosah A ZAROVEN
// vyhladavam pokial som uz nekontroloval koniec chodnika -> to
// by znamenalo, ze uz dokazeme koniec chodnika dosiahnut a tym padom
// sme vyhrali a uz nic vyhladavat nemusime
while (kam_kontroloval < kde_som+v && kam_kontroloval < n+1)
{
// skontroloval som policko - takze hranicu kontroly mozem posunut
// o policko dalej
kam_kontroloval++;
// kontrolujem prave policko, na ktore sme si predtym zaznacili,
// ze padlo zrnko
// tak rovno na to policko skocime!
if (uz_padla[kam_kontroloval])
kde_som = kam_kontroloval;
}
}
}
cout << kde_som << endl;
}
}Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.