2. Trápny vianočný stromček vzorové riešenie

Zadanie

Máme vianočný stromček, ktorý vyzerá ako graf-strom. Na každom vrchole \(v\) je zavesená jedna ozdoba, označená celým číslom \(c_v\).

Občas sa pri stromčeku zastaví okoloidúci. Pozrie sa na cestu z vrcholu \(w\) do \(x\), ďalej sa pozrie na cestu z \(y\) do \(z\), a zamrmle, ako trápny sa mu zdá stromček na základe toho, čo videl. Úroveň trápnosti vypočíta ako počet usporiadaných dvojíc \((i, j)\) spĺňajúcich

• \(i \neq j\)

• Vrchol \(i\) leží na ceste z \(w\) do \(x\).

• Vrchol \(j\) leží na ceste z \(y\) do \(z\).

• Na oboch vrcholoch je zavesená rovnaká ozdoba, teda \(c_i = c_j\).

Úloha

Dostanete popis vianočného stromčeka. Následne príde \(q\) ľudí, a o každom vieme, na ktoré dve úseky sa pozrel. Pre každého zistite, akú úroveň trápnosti dáva stromčeku.

Formát vstupu

Prvý riadok obsahuje dve medzerou oddelené čísla \(n, q\) – počet vrcholov stromu a počet KSPákov.

Druhý riadok obsahuje \(n\) medzerou oddelených celých čísel \(c_1, c_2, \ldots, c_n\) – \(i\)-te z nich je ozdoba zavesená na \(i\)-tom vrchole.

Nasleduje \(n-1\) riadkov. Každý z nich obsahuje dve medzerou oddelené čísla \(u, v\) a popisuje hranu v strome medzi vrcholmi \(u\) a \(v\). Vrcholy sú číslované od \(1\) po \(n\).

Každý z nasledujúcich \(q\) riadkov obsahuje štyri medzerou oddelené čísla \(w, x, y, z\) s rovnakým významom, ako je uvedené vyššie.

Obmedzenia

Vo všetkých sadách platí

• \(1 \leq n \leq 100\,000\)
• \(1 \leq q \leq 50\,000\)
• \(1 \leq c_i \leq 10^9\)
• \(1 \leq u, v, w, x, y, z \leq n\)

Konkrétne obmedzenia pre jednotlivé sady sú

Číslo sady	maximálne \(n\)	maximálne \(q\)
\(1\)	\(50\)	\(10\,000\)
\(2\)	\(300\)	\(300\)
\(3\)	\(5000\)	\(5000\)
\(4, 5\)	\(100\,000\)	\(50\,000\)

Formát výstupu

Pre každého okoloidúceho vypíšte, akú úroveň trápnosti dáva stromčeku.

Príklady

Input:

10 5
10 2 3 5 10 5 3 6 2 1
1 2
1 3
3 4
3 5
3 6
4 7
5 8
7 9
2 10
8 5 2 10
3 8 4 9
1 9 5 9
4 6 4 6
5 8 5 8

Output:

0
1
3
2
0

Strom z príkladu vyzerá nasledovne:

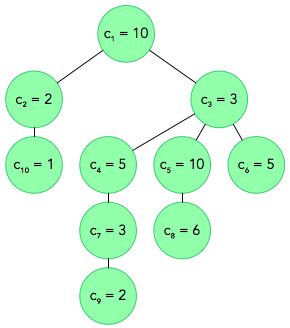
• Prvý okoloidúci sa pozrie na úseky \(8 - 5\) a \(2 - 10\). Vrcholy v prvom úseku majú ale úplne iné ozdoby, ako tie v druhom úseku. Teda trápnosť je \(0\).

• Druhý sa pozrie na úseky \(3 - 8\) a \(4 - 9\). Na vrchole \(3\) aj na \(7\) je zavesená ozdoba \(3\), takže trápnosť je \(1\).

• Tretí sa pozrie na úseky \(1 - 9\) a \(5 - 9\). Dvojice vrcholov s rovnakými ozdobami sú \((1, 5)\), \((3, 7)\) a \((7, 3)\), teda vyhlási trápnosť \(3\).

• Štvrtý sa pozrie dvakrát na ten istý úsek \(4 - 6\). Trápne dvojice sú \((4, 6)\) a \((6, 4)\), teda trápnosť je \(2\).

• Piaty sa tiež dvakrát pozrie na ten istý úsek \(5 - 8\). V ňom majú ale všetky vrcholy rôzne ozdoby, takže trápnosť je \(0\).

Táto úloha sa dala riešiť rôznymi spôsobmi, tu si ukážeme len jeden z nich.

Začnime s tým, že si náš strom zakoreníme (napríklad vo vrchole 1). Koreň nášho stromu označme \(K\). Nech \(\textrm{Ans}(W, X, Y, Z)\) označuje odpoveď na otázku pre cesty z \(W\) do \(X\) a z \(Y\) do \(Z\). Nech \(\textrm{Lca}(X, Y)\) označuje najnižšieho spoločného predka vrcholov \(X, Y\) a nech \(P(X)\) označuje priameho predka vrcholu \(X\). Potom vieme otázku \(\textrm{Ans}(W, X, Y, Z)\) rozbiť nasledovne: \[\textrm{Ans}(W, X, Y, Z) = \textrm{Ans}(W, K, Y, Z) + \textrm{Ans}(K, X, Y, Z) - \textrm{Ans}(\textrm{Lca}(W,X), K, Y, Z) - \textrm{Ans}(K, \textrm{P}(\textrm{Lca}(W,X)), Y, Z) \text{.}\]

Keď rovnakú inklúziu a exklúziu aplikujeme aj na cestu z \(Y\) do \(Z\), rozbijeme našu pôvodnú otázku na \(16\) iných, pre ktoré však bude platiť, že obe cesty majú jeden koniec v koreni. Takýmto spôsobom si teda rozbijeme všetky otázky zo vstupu. Teraz nám stačí už len vyriešiť trochu jednoduchšiu verziu problému, kde v každej otázke obe cesty začínajú v koreni.

Namiesto toho, aby sme postupne spracovávali jednotlivé otázky (ľudí pozerajúcich sa na stromček) a počítali k nim odpovede, budeme postupne spracovávať jednotlivé druhy ozdôb a počítať, ako prispievajú vrcholy s daným druhom ozdoby do odpovedí jednotlivých otázok. Keď spracujeme všetky druhy ozdôb, budeme zároveň vedieť odpovede na jednotlivé otázky.

Čísla (druhy ozdôb), ktoré sa vyskytujú na stromčeku, rozdeľme do dvoch skupín:

• Časté : čísla, ktoré sa v strome vyskytujú aspoň \(\sqrt{n/\log n}\)-krát¹.
• Zriedkavé : čisla, ktoré sa na strome vyskytujú menej ako \(\sqrt{n/\log n}\) krát.

S každou skupinou čísel sa vysporiadame inak.

Časté čísla

Keďže každé časté číslo sa v strome vyskytuje veľakrát, týchto čísel bude málo. Preto môžeme na každom z nich stráviť pomerne veľa času. Pre každé časté číslo \(c\) teda môžeme spraviť na našom strome jedno DFS, v ktorom si pre každý vrchol vypočítame, koľkokrát sa vyskytuje číslo \(c\) na ceste z tohto vrchola do koreňa. Následne už pre každú otázku vieme vypočítať, ako do jej odpovede prispeje \(c\): v konštantnom čase zistíme, koľko \(c\)-čok leží na jednej, a koľko na druhej ceste, a tieto dve čísla nám stačí vynásobiť. Nakoniec ešte bude treba odčítať počet \(c\)-čok, ktoré ležali na prieniku ciest (lebo dvojice obsahujúce ten istý vrchol dvakrát podľa zadania nemáme počítať).

Každé časté číslo takto vieme spravocať v čase \(O(n + q)\). Keďže častých čísel bude najviac \(n / \sqrt{n/\log n} = \sqrt{n \log n}\), spracovanie všetkých častých čísel bude dokopy trvať \(O((n+q) \sqrt{n \log n})\).

Zriedkavé čísla

Najprv si prejdeme celým stromom a pre každé zriedkavé číslo si poznačíme, kde všade (v ktorých vrcholoch) sa toto číslo vyskytuje.

Vrcholy nášho (zakoreneného) stromu si môžeme očíslovať v preorder poradí (teda v poradí, v akom ich navštívi DFS). Toto poradie má jednu peknú vlastnosť: pre každý podstrom platí, že čísla vrcholov tohto podstromu tvoria súvislú postupnosť. Inými slovami, sú to všetky celé čísla z nejakého intervalu.

Každá otázka je daná štyroma vrcholmi: koncami ciest, na ktoré sa táto otázka pýta. Keďže však dva z týchto vrcholov sú vždy koreň nášho stromu, reálne je každá otázka určená iba dvoma vrcholmi. Ak sa na čísla týchto vrcholov (v našom novom preorder číslovaní) budeme pozerať ako na súradnice, na každú otázku sa môžeme pozerať ako na bod v dvojrozmernom priestore.

Nech \(c\) je teraz nejaké zriedkavé číslo. Pre každú dvojicu vrcholov, ktoré v sebe majú ozdobu typu \(c\), sa pozrieme, ktoré otázky ovplyvnia. Nech \(U\) a \(V\) je nejaká dvojica vrcholov typu \(c\). Táto dvojica prispieva do odpovedí práve tých otázok, ktorých jedna cesta končí v podstrome pod \(U\) a druhá v podstrome pod \(V\). To znamená, že koniec jednej cesty musí mať číslo z intervalu zodpovedajúceho podstromu \(U\) a koniec druhej musí mať číslo z intervalu zodpovedajúceho podstromu \(V\). V našej geometrickej predstave tomu zodpovedajú body ležiace vnútri nejakého obdĺžnika. Všetkým otázkam z tohto obdĺžnika by sme teda chceli zvýšiť odpoveď o \(1\). To však neurobíme hneď. Namiesto toho si iba zapamätáme súradnice tohto obdĺžnika.

Takto prejdeme všetky dvojice vrcholov, obsahujúcich rovnaké zriedkavé číslo a pre každú z nich dostaneme jeden obdĺžnik. Týchto obdĺžnikov bude dokopy najviac \(n \sqrt{n/ \log n}\), pretože každý vrchol bude v najviac \(\sqrt{n/ \log n}\) rôznych dvojiciach (keďže inak by už jeho číslo muselo byť časté a nie zriedkavé).

Máme teda zhruba \(n \sqrt{n/ \log n}\) obdĺžnikov a \(q\) bodov a pre každý bod nás zaujíma, v koľkých obdĺžnikoch leží. Všetky súradnice sú pritom celé čísla z rozsahu \(1\) až \(n\). Takáto úloha sa dá vyriešiť zametaním za pomoci intervalového stromu (treba strom s lazy propagation), v čase \(O((q + n \sqrt{n/ \log n})\log n) = O(q \log n + n \sqrt{n \log n})\).

Celá úloha sa dá teda vyriešiť v čase \(O((n+q) \sqrt{n \log n})\).