Zadanie
V dávnych časoch, na ktoré sa v KSP pamätá už len Mišof, sa snažil Dávidko1 rozbehnúť start-up so špeciálnymi ‘Dávidkovými procesormi’. V tom čase predstavovali so svojou 32 bitovou výpočtovou jednotkou a takmer 77 MB pamäťou vrchol technického pokroku. Bohužiaľ, kvôli slabej mediálnej kampani neboli tieto procesory úspešné a celý Dávidkov projekt zapadol prachom.
Nedávno, prehrabávajúc sa zákutiami T2, objavil tento projekt Syseľ a povedal si, že teraz by už mohol dopadnúť lepšie. Ísť však na trh s procesorom by nebolo príliš rozumné. Ak by však daný procesor upravil tak, aby vedel komprimovať text, tak by ‘Sysľov komprimátor’ mohol zožať nečakaný úspech. Akurát tá úprava nie je taká jednoduchá, keďže ‘Dávidkov procesor’ beží na veľmi starom a primitívnom systéme. Vy si s tým však určite nejak poradíte.
Dávidkov procesor
Dávidkov procesor obsahuje jeden zásobník (stack), s ktorým pracujú dané inštrukcie. Na zásobník sa ukladajú 32-bitové čísla so znamienkom, teda čísla z rozsahu \(-2^{31}\) až \(2^{31}-1\). Na začiatku behu programu je zásobník prázdny.
Zásobník zapisujeme horizontálne, pričom napravo sa nachádza vrch zásobníka. Reťazec "..." reprezentuje pôvodný stav zásobníka. Reťazec "...|a|b" značí, že na vrchu zásobníka sa nachádza číslo \(b\) a pod ním číslo \(a\). Hodnota "S[n]" je \(n\)-tá hodnota zásobníka. Ak je \(n\geq 0\) táto hodnota sa počíta od spodku, ak \(n<0\), tak od vrchu.
Dávidkov procesor pozná nasledovné príkazy:
| Príkaz | Popis príkazu | Zásobník pred | Zásobník po |
|---|---|---|---|
| PUSH\(~~const\) | Na vrch zásobníka pridá číselnú konštantu \(const\) | … | …|const |
| OUT | Odstráni vrchné číslo zásobníka a vypíše ho na výstup ako ASCII | …|a | … |
| znak. Chyba nastane, ak je odstránené číslo menšie ako 0 alebo | |||
| väčšie ako 127. | |||
| READ | Odstráni zo zásobníka vrchné číslo (označme ho \(a\)) a následne | …|a | …|S[a] |
| nakopíruje na vrch zásobníka hodnotu \(S[a]\) | |||
| JGZ | Odstráni zo zásobníka dve vrchné hodnoty \(b\) a \(a\). Následne sa | …|a|b | … |
| posunie o \(b\) inštrukcií (dopredu pre kladné \(b\), inak dozadu) | |||
| v prípade, že je \(a>0\) | |||
| ADD | Odstráni dve čísla na vrchu zásobníka a pridá na vrch ich súčet | …|a|b | …|a+b |
| MUL | Odstráni dve čísla na vrchu zásobníka a pridá na vrch ich súčin | …|a|b | …|a*b |
| DIV | Odstráni dve čísla na vrchu zásobníka a na vrch pridá ich podiel | …|a|b | …|q|r |
| a zvyšok po delení (\(q=a/b\) (celočíselné delenie), \(r=a\%b\)) |
Ak by pri vykonávaní niektorého príkazu nebolo v zásobníku dostatočné množstvo čísel (napríklad aspoň 2 pre JGZ, aspoň 1 pre OUT), program skončí chybou. Program tiež skončí chybou, ak je na zásobníku v niektorom momente viac ako \(20\,000\,000\) čísel, alebo sa vykoná viac ako \(300\,000\,000\) príkazov.
Technické detaily aritmetických operácií (pretečenie, modulo zo záporného čísla atď.) fungujú rovnako ako v C++.
Program si po spustení udržiava hodnotu \(prikaz\), ktorá ukazuje na príkaz, ktorý sa aktuálne vykonáva. Táto hodnota je na začiatku 0 (začína sa prvým príkazom). Hodnota \(prikaz\) sa zvýši o 1 po dokončení aktuálneho príkazu. Ak nastal skok príkazom "JGZ", táto premenná sa ešte predtým zmení o danú veľkosť skoku \(b\), následne sa však opäť posunie o 1 dopredu. Ak teda \(b=-1\), tak \(prikaz\) bude ukazovať opäť na ten istý príkaz. V okamihu ako premenná \(prikaz\) ukazuje mimo existujúce príkazy, program je považovaný za korektne zastavený.
Úloha
Dávidkov procesor podporuje iba uvedenú malú sadu príkazov. Vašou úlohou je pomocou týchto príkazov napísať čo najkratší program, ktorý vypíše zadaný text.
Formát vstupu
Dostanete 9 rôznych súborov s textami, všetky používajú štandardnú 7-bitovú ASCII reprezentáciu znakov. Niektoré z textov sú zmysluplné anglické alebo slovenské texty, iné sú vytvorené umelo. Súbory so vstupmi majú názvy 1.in, 2.in, … , 9.in.
Formát výstupu
Odovzdajte jeden ZIP archív, ktorý bude obsahovať súbory s názvami 1.out, 2.out, … , 9.out. Pre každý vstupný text teda odovzdávate samostatný súbor s programom pre Dávidkov procesor.
Každý súbor sa musí skladať z príkazov popísaných vyššie a vypísať daný text. Odovzdaný program je zoznam inštrukcií, každá na samostatnom riadku. Inštrukcie píšte veľkými písmenami presne ako sú udané v tabuľke.
Uvedomte si, že vašou úlohou je vypísať presne taký istý text, vrátane znakov ako medzery alebo konce riadkov. Prvé 4 vstupy neobsahujú znak konca riadka.
Hodnotenie
Každý z deviatich textov bude hodnotený samostatne. Za vyriešenie každého z nich sa dá získať nejaká časť bodov a výsledný bodový zisk je súčet bodov za každý text.
| Text | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Maximálny počet bodov | 1 | 2 | 2 | 3 | 3 | 3 | 4 | 3 | 4 |
V tejto úlohe budete súťažiť proti sebe. Bodovanie v rámci jedného textu je škálované podľa najlepšieho odovzdaného riešenia.
Skóre odovzdaného programu sa vypočíta ako počet inštrukcií použitých v programe (teda počet príkazov v zdrojovom kóde, nie počet príkazov, ktoré sa naozaj vykonajú počas behu programu), pričom príkaz "PUSH" sa počíta za 2. Nech \(O\) je skóre programu, ktorý ste odovzdali, \(M\) je najmenšie dosiaľ získané skóre nejakého programu (vrátane toho so skóre \(O\)) a \(B\) je počet bodov, ktoré sa dajú získať za vyriešenie daného textu. Výsledného skóre tohto programu je \(B\cdot \frac{M}{O}\).
Počas behu kola budeme hodnoty \(M\) (najmenšie dosiahnuté skóre pre každý text) aktualizovať približne raz za týždeň a po skončení kola ich aktualizujeme znova a vypočítame finálne body.
Keďže neodovzdávate programy a nás zaujíma, ako úlohu riešite, môžete do ZIPka priložiť aj zdrojové kódy programov, ktoré ste pri riešení použili, prípadne stručný popis, ak by ste sa chceli pochváliť.
Súbory na stiahnutie
Na tomto odkaze: http://media.ksp.sk/ulohy/34rocnik/1kolo/prikl8-na-stiahnutie.zip si viete stiahnuť niekoľko užitočných súborov. Je tam spomínaných deväť textov, pre ktoré máte vytvoriť programy a takisto C++ program, ktorý simuluje tento zásobníkový procesor. Vďaka nemu si viete otestovať, či vami vytvorený program naozaj vypíše žiadaný text. Rovnakým spôsobom budeme tiež simulovať vaše riešenia na testovači, takže si môžete overiť implementáciu dôležitých častí zásobníkového procesora.
Príklad
Input:
HelloOutput:
PUSH 72
OUT
PUSH 203
PUSH 2
DIV
PUSH 2
JGZ
PUSH 80
OUT
OUT
PUSH 108
PUSH 111
PUSH 0
PUSH 0
READ
OUT
READ
OUT
OUTVšimnite si, že príkazy na riadkoch 7 a 8 (číslujeme od 0) boli preskočené vďaka "JGZ" a nikdy sa nevykonali. Program skončil korektne a na zásobníku ostalo číslo 108. Skóre takéhoto programu je 28.
Bývalý KSP vedúci, ktorý aktuálne pracuje v New Yorku a má manželku Halucinku (ďalšia bývalá KSP vedúca).↩
Dúfam, že so mnou budete súhlasiť v tom, že táto optimalizačná úloha bola naozaj zaujímavá. Nestáva sa predsa každý deň, že píšete program, ktorého výstupom je iný program. Otázkou však je, ako napísať k takejto úlohe vzorák.
Nakoniec som sa rozhodol, že vám v tomto vzoráku ukážem hlavné myšlienky, ktorými sa dalo riadiť pri postupnom získavaní bodov. Najprv si ukážeme niekoľko jednoduchších prístupov, potom si predstavíme pomerne zaujímavý algoritmus slúžiaci na kódovanie znakov a nakoniec to všetko skombinujeme do výsledného riešenia. To samozrejme nebude najlepšie možné, ale kvôli prehľadnosti vzorového riešenia nebudeme uplatňovať príliš veľa optimalizácií.
S niečím začať treba
Prečo teda nespraviť prvú a najľahšiu vec, čo nám napadne! Nemáme čo stratiť a naprogramovanie ľahkého riešenia nám zaberie veľmi málo času. Otestujeme si ním, či správne rozumieme príkazom, ktoré Dávidkov procesor používa, a keď budeme neskôr robiť niečo zložitejšie, budeme si vedieť porovnať naše riešenia a zistiť, ako veľmi sme sa zlepšili.
Ak sa pozrieme na príkazy, ktoré používa Dávidkov procesor, vidíme, že vypisovať budeme príkazom OUT. Ten podľa zadania zoberie vrchné číslo na zásobníku a vypíše toľký znak z ASCII tabuľky. Ak teda chceme napríklad vypísať znak "a", ktorý je v ASCII tabuľke 97-my, tak najskôr musíme dostať na zásobník číslo 97, čo spravíme príkazom PUSH 97. Takto vieme dostať jednoduchý program, ktorý vypíše znak "a" a nič iné.
PUSH 97
OUT
A toto predsa vieme spraviť s ľubovoľným znakom v texte. Pozrieme sa na to, koľký v poradí je tento znak v ASCII tabuľke, vložíme také číslo do zásobníka a potom ho z neho rovno vypíšeme. Môžeme preto napísať jednoduchý program v C++, ktorý načíta text a vytvorí z neho program pre Dávidkov procesor, ktorý daný text vypíše.
Všimnite si, ako v tomto programe šikovne využívame fakt, že C++ vie s premennou typu char pracovať ako s číslom z ASCII tabuľky. Ak preto necháme vypísať char ako int, vypíše sa žiadaná hodnota.
#include <cstdio>
using namespace std;
int main() {
char c;
while(scanf("%c", &c) == 1) {
printf("PUSH %d\n", c);
printf("OUT\n");
}
}Programovanie v Dávidkovom procesore
Ukázali sme si, ako vieme spraviť prvé, veľmi jednoduché riešenie, ktoré pre každý znak na vstupe použije dva príkazy Dávidkovho procesora. Ďalej potrebujeme prísť s niečím, čo tento počet príkazov výrazne zmenší. To, že musíme pridať na zásobník konkrétnu hodnotu pre každý znak asi neovplyvníme (zatiaľ). Mohli by sme však radšej použiť ostatné príkazy Dávidkovho procesora na to, aby sme zmenšili počet príkazov potrebných na vypisovanie.
Čo spravíme v C++, ak chceme vypísať obsah nejakého poľa (zásobníka)? Použijeme for-cyklus. Hľadáme preto spôsob, akým naprogramovať for-cyklus v Dávidkovom procesore. A keďže for-cyklus nie je nič iné ako vracanie sa na tie isté riadky, budeme chcieť použiť príkaz JGZ.
Rozmyslime si najskôr slovne, čo chceme spraviť: “Vypíš znak zodpovedajúci vrchnému číslu na zásobníku a toto číslo odstráň. Ak zásobník nie je prázdny, vráť sa na príkaz výpisu (začiatok).”
Hneď si však všimneme, že nevieme zistiť, či je zásobník prázdny alebo nie. Vieme iba zisťovať, či je na vrchu zásobníka číslo väčšie ako 0. A keďže 0 sa medzi číslami na zásobníku nachádzať nebude (lebo to nie je znak, ktorý by sa nám objavil v texte), môže 0 slúžiť ako vhodná zarážka na koniec zásobníka. Potrebujeme preto overiť, či je na vrchu zásobníka 0 a ak nie je, tak pokračovať vo vypisovaní.
Posledný problém, ktorý musíme vyriešiť, je, že príkaz JGZ odstráni dve vrchné čísla zo zásobníka. Musíme si preto vytvoriť kópiu vrchného čísla, ktorú môžeme bez problémov odstrániť. Takúto kópiu vytvoríme pomocou príkazu READ.
OUT
PUSH -1
READ // nakopíruj číslo na pozícii -1 (teda to najvrchnejšie) na vrch zásobníka
PUSH -5 // o koľko príkazov sa chcem vrátiť, ak číslo navrchu nie je 0
JGZ // ak druhé číslo zvrchu zásobníka nie je 0, tak program
// sa vráti o 5 inštrukcií späť, čo je práve príkaz OUT
To, čo sme spravili, je vlastne programovanie pomocou príkazov Dávidkovho procesora. Poriadne si pozrite vyššie uvedený program. Niečo podobné ešte párkrát uvidíte a v podstate nič zložitejšie potrebovať nebudeme.
Náš program teda do zásobníka postupne pridá jedno číslo za každý znak textu a potom vykoná vyššie uvedený kúsok programu, ktorý znaky vypíše. Netreba ešte zabudnúť na to, že čísla znakov musíme na zásobník pridávať v obrátenom poradí, teda prvý znak textu musí byť pridaný ako posledný.
Štyri v jednom
Koľko príkazov použil náš posledný program? Potreboval jeden príkaz za každé písmeno na vstupe a potom ešte päť príkazov na vypísanie. Asi je jasné, že ak chceme vymyslieť ešte lepšie riešenie, musíme zmenšiť počet čísel, ktoré na začiatku vložíme do zásobníka.
To znamená, že jedno číslo musí zastupovať (kódovať) viacero znakov. Uvedomme si, že čísla, ktoré môžeme vkladať do zásobníka môžu mať veľkosť až \(2^{31}-1\). Naše riešenia však zatiaľ používali iba čísla, ktoré nemohli byť väčšie ako \(2^7\) (počet znakov v ASCII tabuľke). Pokúsime sa preto nájsť spôsob, akým zakódovať viacero znakov do jedného čísla a samozrejme aj spôsob, ako tento postup obrátiť (ako z čísla zistiť znaky, ktoré kóduje).
Predstavme si, že chceme zakódovať dva znaky – znak "a" s ASCII číslom 97 a znak "b" s ASCII číslom 98, pričom "a" má byť vypísané skôr ako "b". Použime na to číslo \(12\,641 = 128\cdot 98 + 97\). Dôvod, prečo je takéto kódovanie dobré je ten, že z čísla \(12\,641\) vieme ľahko zistiť, ktorý znak má byť vypísaný prvý. Bude to predsa zvyšok čísla \(12\,641\) po delení \(128\). Druhé číslo na vypísanie bude celočíselný podiel týchto dvoch čísel a na počítanie podielu a zvyšku po delení máme pre Dávidkov procesor príkaz DIV.
Nemusíme sa však obmedziť tým, že do jedného čísla zakódujeme len dva znaky. Takéto čísla budú totiž nanajvýš veľkosti \(2^{14}\). Pridajme preto rovnakým spôsobom ďalšie dve čísla. Zo štyroch znakov \(a\), \(b\), \(c\) a \(d\) (toto sú premenné a nie konkrétne znaky) potom vieme spraviť jedno číslo menšie ako \(2^{28}\) nasledovne:
\[a + 128\cdot b + 128^2 \cdot c + 128^3 \cdot d\]
Sami si rozmyslite, že postupným delením tohto čísla číslom 128 budeme ako zvyšky dostávať čísla zodpovedajúce znakom \(a\), \(b\), \(c\) a \(d\).
Program, ktorý kóduje náš text takýmto spôsobom je o niečo komplikovanejší. Musíme si dať pozor, aby sme zakódovali čísla v správnom poradí a musíme vymyslieť program používajúci príkazy Dávidkovho procesora, ktorý bude zadané čísla deliť 128 a vypisovať ich na výstup. Nie je to však až také ťažké a nižšie si môžete pozrieť jedno možné riešenie.
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
int main() {
vector<char> Text;
char c;
while (scanf("%c", &c) == 1) Text.push_back(c);
while (Text.size() % 4 != 0) Text.push_back(0); // doplním pole Text o nejaké 0, aby mal správnu dĺžku
reverse(Text.begin(), Text.end());
printf("PUSH 0\n"); // zarážka na spodok zásobníka
for(int i = 0; i < Text.size()/4; i++)
printf("PUSH %d\n",128*128*128*Text[4*i] + 128*128*Text[4*i+1] + 128*Text[4*i+2] + Text[4*i+3]);
printf("PUSH 128\n");
printf("DIV\n");
printf("OUT\n");
printf("PUSH -1\n");
printf("READ\n");
printf("PUSH -7\n");
printf("JGZ\n");
// ak sa program dostane až sem, znamená to, že číslo
// na vrchu sme vydelili už 4 krát a musíme ho zásobníka vyhodiť
printf("ADD\n");
printf("PUSH -1\n");
printf("READ\n");
printf("PUSH -12\n");
printf("JGZ\n");
}Tok bitov
Pokúsime sa ešte viac vylepšiť naše riešenie. Dobrý nápad je pozrieť sa na jednotlivé texty, ktoré máme zadané. Možno nás napadne nejaké lepšie riešenie, našité priamo na ne.
A naozaj, ak sa pozrieme na text 1.in, zistíme, že obsahuje iba písmená "c" (dokonca neobsahuje ani koniec riadku). Je zjavne zbytočné do zásobníka vkladať veľa hodnôt, ktoré nám aj tak povedia to, čo už dopredu vieme – vypíš písmeno "c". Namiesto toho by nám v zásobníku mohla stačiť iba jedna hodnota, ktorá hovorí, koľko písmen "c" ešte máme vypísať. Túto hodnotu budeme postupne znižovať až kým neklesne na 0. Vtedy program ukončíme pomocou príkazu JGZ.
Dostaneme jednoduchý 9-príkazový program:
PUSH 9379
PUSH 99
OUT
PUSH -1
ADD
PUSH -1
READ
PUSH -8
JGZ
Pozrime sa teraz na text 2.in. V ňom sa nachádzajú iba dva druhy písmen – "f" a "y". Naším cieľom bude teda zakódovať túto postupnosť dvoch druhov písmen čo najúspornejšie. Predchádzajúce všeobecné riešenie používalo na kódovanie čísla 102 a 121. To je však strašne zbytočné. Na zakódovanie písmena "f" môžeme predsa použiť hodnotu 0 a ako kód "y" použijeme 1. Záleží len na nás, či bude náš program rozoznávať "f" ako 102 alebo 0.
Náš text sme si teda zmenili na postupnosť bitov (základná jednotka informácie, ktorá nadobúda iba hodnotu 0 alebo 1) – a v počítači je aj každé číslo reprezentované ako postupnosť bitov (v našom prípade 32 bitov). Namiesto 4 písmen vieme teraz do jedného čísla preto zakódovať až 32 písmen, čo je 8-násobné zlepšenie.
Napriek tomu, to nebude také jednoduché. Po prvé, potrebujeme do čísla zakódovať nejakým spôsobom túto postupnosť bitov. To síce vyzerá priamočiaro – nasekám si bity na 32-tice a jednoducho ich zmením na číslo – avšak objaví sa niekoľko problémov, ktoré budeme musieť vyriešiť. Po prvé, je nebezpečné používať všetkých 32 bitov, lebo hoci Dávidkov procesor dokáže pracovať s \(2^{32}\) číslami, polovica z nich je záporná (rozsah čísel v zásobníku je \(-2^{31}\) až \(2^{31}-1\)). Tu by už naša matematika – delíme 2 a pozeráme sa na zvyšok – nefungovala tak akoby sme chceli, a preto sa obmedzíme len na prvých 31 bitov, ktoré nám zaručia, že čísla budú kladné.
Navyše však dostaneme nasledovný problém. Náš program bude postupne deliť naše číslo hodnotou 2. Kedy má však zastať? Ak sa číslo zmenší na 0, znamená to, že už som spracoval všetky bity, alebo ešte nasleduje niekoľko 0-vých bitov? Riešení tohto problému môže byť viac. Pri jednom možnom spôsobe zopakujeme Dávidkovým programom 31 delení. Mohli by sme 31-krát nakopírovať kus programu ktorý vykoná delenie alebo na to použiť ďalší (vnorený) cyklus. Buď sa nám teda zväčší počet príkazov, alebo to bude neprehľadnejšie a takisto budeme musieť ešte vyriešiť prípad, kedy niektoré číslo nekóduje 31, ale menej bitov.
Riešenie, ktoré si ale ukážeme my, bude založené na tom, že si do každého čísla spravíme značku. V podstate si vyhradíme najvyšší používaný bit (väčšinou 31-vý) ako zarážku. Zakaždým bude mať hodnotu 1. Tým pádom, pri delení dvojkou sa nám raz stane, že nám v celom čísle ostane už len tento jednotkový bit, a číslo, ktoré budeme spracovávať bude teda rovné 1. Ak nastane takýto prípad, budeme vedieť, že už sme spracovali všetky bity, ktoré kódovalo toto číslo a môžeme sa presunúť na to ďalšie.
Pozrite si nižšie uvedenú implementáciu takéhoto riešenia. Všimnite si hlavne časť, v ktorej je zadrôtovaný Dávidkov program, ktorý vydelí číslo hodnotou 2 a podľa zvyšku skočí buď do časti, ktorá vypisuje písmeno "f" alebo do časti pre písmeno "y".
#include <cstdio>
#include <string>
#include <algorithm>
#include <vector>
#include <cmath>
using namespace std;
vector<char> Text;
int main() {
// načítam text
char c;
while(scanf("%c", &c) == 1) Text.push_back(c);
//zmením text na postupnosť 0 a 1
string tok_bitov = "";
for(int i = 0; i < Text.size(); i++)
if(Text[i] == 'f') tok_bitov += "0";
else tok_bitov += "1";
reverse(tok_bitov.begin(), tok_bitov.end());
printf("PUSH 0\n"); // zarážka na spodok zásobníka
// zakódujem 30 bitov do jedného čísla, ktoré vložím na zásobník
int kolko = 0, cislo = 1;
for(int i = 0; i < tok_bitov.size(); i++) {
cislo *= 2;
cislo += tok_bitov[i] - '0';
kolko++;
if(kolko == 30 || i == tok_bitov.size()-1) {
printf("PUSH %d\n",cislo);
cislo = 1; kolko = 0;
}
}
// skontrolujem, či v čísle už nezostala len 1 a nepotrebujem ďalšie číslo
// potom skontrolujem, či na vrchu nie je 0 a nemám už skončiť
printf("PUSH -1\n");
printf("READ\n");
printf("PUSH -1\n");
printf("ADD\n");
printf("PUSH 8\n");
printf("JGZ\n");
printf("MUL\n");
printf("PUSH -1\n");
printf("READ\n");
printf("PUSH 3\n");
printf("JGZ\n");
printf("PUSH 1\n");
printf("PUSH 1000000\n");
printf("JGZ\n");
// pozriem sa na posledný bit aktuálneho čísla
printf("PUSH 2\n");
printf("DIV\n");
printf("PUSH 5\n"); // ak je to 1, chcem preskočiť 5 príkazov
printf("JGZ\n");
printf("PUSH 102\n"); // ak som neskončil, tak tam bola 0
printf("OUT\n");
printf("PUSH 1\n");
printf("PUSH -23\n"); // skoč na začiatok
printf("JGZ\n");
printf("PUSH 121\n");
printf("OUT\n");
printf("PUSH 1\n");
printf("PUSH -28\n"); // skoč na začiatok
printf("JGZ\n");
}Uvedomme si ešte, že takéto riešenie sa dá istým spôsobom zovšeobecniť. Na vstupe máme postupnosť (tok) bitov. Našou úlohou je spracovávať ich jeden po druhom a robiť rozhodnutia podľa toho, či je aktuálny bit 0 alebo 1. To, čo sme si ukázali v tejto časti, boli často len technické pomôcky, ako niečo takéto robiť pomocou príkazov Dávidkovho procesora.
Nerovnomerný výskyt a prefixový kód
Pozrime sa teraz na text 4.in1. V ňom sa objavujú len tri znaky – "p", "q" a "A".
Prirodzene, prvá vec, ktorá nám napadne, je použiť na kódovanie znakov čísla 0, 1 a 2 (v jednom čísle by sme si pamätali znaky nie ako zvyšky po opakovanom delením dvomi, ale po delení tromi). Na tom by nebolo nič zlé, ale predsa len, zaberá to trochu veľa miesta – na každé číslo musíme využiť takmer 2 bity.
Zostaňme ale pri našej predstave toku bitov s hodnotami 0 alebo 1. Mohli by sme napríklad každému znaku priradiť nejaké dva bity (napr.: "p" by sme zakódovali ako "00", "q" ako "01" a "A" ako "10"). Potom by sme opäť dostali tok bitov, akurát by sa trochu nepríjemnejšie spracovával. Ale to nám tiež neušetrí počet bitov, ktoré použijeme. Skúsme to ešte inak. Použime na kódovanie tri, nerovnako dlhé, reťazce "1", "00" a "01".
Keď každému písmenu priradíme jeden takýto reťazec, opäť vieme celý text zmeniť na postupnosť bitov. Naviac, táto postupnosť bitov sa dá jednoducho dekódovať. Postupne prechádzame bity zľava – ak je prvý bit 1, vieme, že sme narazili na prvé písmeno a môžeme ho vypísať. Ak je prvý bit 0, tak zase vieme, že sa musíme pozrieť ešte na druhý bit a až ten nám rozhodne, čo máme vypísať. V každom momente sa preto vieme jednoznačne rozhodnúť, čo treba spraviť. Naviac, na zakódovanie jedného zo znakov použijeme iba jeden bit.
To, čo môžeme v takomto riešení ovplyvniť je, ktorým písmenám priradíme ktorý reťazec. Už pri letmom pohľade do textu 4.in by sme si mali všimnúť, že znak "A" sa tam nachádza častejšie. Je preto logické, že práve jemu chceme priradiť reťazec "1", lebo ušetrenie jedného bitu (oproti reťazcom "01" a "00") bude častejšie. Na priradení zvyšných dvoch reťazcov nezáleží, lebo majú rovnakú dĺžku.
Následne ešte musíme trochu upraviť Dávidkov program, ktorý bude tento tok bitov spracovávať. Aj on sa totiž musí vedieť rozhodovať podľa toho, či vidí 0 alebo 1 a ak vidí 0 tak sa presunúť na ďalší bit, aby vedel, čo má vypísať. Riešenie je však veľmi podobné tomu, čo sme už videli predtým. Všimnite si, že Dávidkov program aj pre prehľadnosť rozdeľujem do častí, medzi ktorými náš program skáče a každá časť má presne určenú úlohu.
#include <cstdio>
#include <string>
#include <algorithm>
#include <vector>
#include <cmath>
using namespace std;
vector<char> Text;
int main() {
// načítam text
char c;
while(scanf("%c", &c) == 1) Text.push_back(c);
//zmením text na postupnosť 0 a 1
string tok_bitov = "";
for(int i = 0; i < Text.size(); i++)
if(Text[i] == 'A') tok_bitov += "1";
else if(Text[i] == 'p') tok_bitov += "00";
else tok_bitov += "01";
reverse(tok_bitov.begin(), tok_bitov.end());
// zarážka na spodok zásobníka
printf("PUSH 0\n");
// zakódujem 30 bitov do jedného čísla, ktoré vložím na zásobník
int kolko = 0, cislo = 1;
for(int i=0; i < tok_bitov.size(); i++) {
cislo *= 2;
cislo += tok_bitov[i]-'0';
kolko++;
if(kolko == 30 || i == tok_bitov.size()-1) {
printf("PUSH %d\n", cislo);
cislo = 1; kolko = 0;
}
}
// skontrolujem, či v čísle už nezostala len 1 a nepotrebujem ďalšie číslo
// potom skontrolujem, či na vrchu nie je 0 a nemám už skončiť
printf("PUSH -1\n");
printf("READ\n");
printf("PUSH -1\n");
printf("ADD\n");
printf("PUSH 8\n");
printf("JGZ\n");
printf("MUL\n");
printf("PUSH -1\n");
printf("READ\n");
printf("PUSH 3\n");
printf("JGZ\n");
printf("PUSH 1\n");
printf("PUSH 1000000\n");
printf("JGZ\n");
// pozriem sa na posledný bit aktuálneho čísla
printf("PUSH 2\n");
printf("DIV\n");
printf("PUSH 21\n");
printf("JGZ\n");
// posledný bit bola 0, takže sa musím pozrieť na ďalší
// najskôr sa pozriem, či som ešte neminul toto číslo
printf("PUSH -1\n");
printf("READ\n");
printf("PUSH -1\n");
printf("ADD\n");
printf("PUSH 1\n");
printf("JGZ\n");
printf("MUL\n");
// pozriem sa na ďalší bit
printf("PUSH 2\n");
printf("DIV\n");
printf("PUSH 5\n");
printf("JGZ\n");
// vypíšem znak p za 00
printf("PUSH 112\n");
printf("OUT\n");
printf("PUSH 1\n");
printf("PUSH -34\n");
printf("JGZ\n");
// vypíšem znak q za 01
printf("PUSH 113\n");
printf("OUT\n");
printf("PUSH 1\n");
printf("PUSH -39\n");
printf("JGZ\n");
// vypíšem znak A za 1
printf("PUSH 65\n");
printf("OUT\n");
printf("PUSH 1\n");
printf("PUSH -44\n");
printf("JGZ\n");
}Na tomto riešení si môžeme všimnúť dve veľmi dôležité veci. Prvou je, že reťazce, ktoré priraďujeme ako kódy znakov nemusia byť rovnako dlhé. Prirodzene sa nám potom oplatí použiť kratšie reťazce pre častejšie sa vyskytujúce znaky, keďže vďaka tomu viac ušetríme. Takýto postup využíva napríklad aj Morseovka. Ak si pozriete tabuľku jej kódovania, zistíte, že dva najkratšie reťazce, bodka a čiarka, sú priradené písmenám "E" a "T", ktoré sú (nie zhodou náhod) dve najčastejšie sa vyskytujúce písmená anglickej abecedy. Najdlhšie reťazce sú naopak priradené znakom, ktoré sa vyskytujú veľmi zriedkavo.
To však nebola jediná vec, na ktorú sme si museli dať pozor. Je potrebné tiež zaručiť, že dekódovanie je jednoznačné – teda vždy máme na základe aktuálneho bitu iba jedinú možnosť na to, čo spraviť. V Morseovke takéto niečo neplatí, ak sa pri dekódovaní objaví ako prvá bodka, nemôžeme si byť istí, či máme vypísať "E" (bodka), alebo prečítať ďalší znak, ktorý môže byť čiarka, čo by zodpovedalo písmenu "A" (bodka, čiarka). V Morseovke sa preto používa aj tretí symbol – oddeľovač.
My však oddeľovač k dispozícii nemáme (máme iba znaky 0 a 1), preto budeme používať prefixové kódy. To znamená, že žiaden kód nie je prefixom (začiatkom) iného kódu. Keď je splnená táto podmienka, kód sa bude dať vždy jednoznačne dekódovať.
Huffmanov kód
Zoberme si teraz ľubovoľný text, napríklad jeden z posledných štyroch – anglické a slovenské texty. Naším cieľom je vytvoriť prefixový kód, ktorý naviac zakóduje náš text na čo najmenej bitov. Uvedomte si, že takýto kód chceme našiť priamo na daný text, lebo výskyty písmen ovplyvňujú dĺžku kódových slov. V slovenčine totiž asi ťažko budeme hľadať písmená "q" alebo "w" a ak sa aj vyskytnú, môžeme im priradiť naozaj dlhý kód. V angličtine sú však tieto dve písmená oveľa častejšie a naše riešenie by to malo zobrať do úvahy. Hľadáme preto všeobecný algoritmus, ktorý dokáže pre daný text vytvoriť prefixový kód s optimálnou dĺžkou.(Kód je jedno konkrétne priradenie kódových slov (v našom prípade binárnych reťazcov) znakom textu.)
Zoberme si konkrétny text a spočítajme si písmená, ktoré obsahuje. Nech obsahuje \(m\) písmen, pričom \(i\)-te písmeno sa v tomto texte vyskytuje \(p_i\)-krát. Naviac, nech platí \(p_0 \geq p_1 \geq \dots \geq p_m\). Predstavme si tiež, že už máme nájdený optimálny prefixový kód, ktorý týmto znakom priradí binárne kódy \(w_1, w_2 \dots w_m\). Naviac, dĺžky týchto kódových slov si označme \(l_1, l_2 \dots l_m\).
Z tohto vyplýva, že na zakódovanie tohto textu potrebujeme presne \(\sum_{i=1}^m p_i\cdot l_i\) bitov. Poďme si povedať, čo musí platiť o týchto slovách, ak majú tvoriť optimálny kód. Po prvé, musí platiť, že \(l_1 \leq l_2 \leq \dots \leq l_m\). Toto zodpovedá nášmu pozorovaniu, že dlhšie kódové slová chceme priraďovať menej častým znakom. Teraz si to však vieme aj dokázať. Ak by to totiž pre nejaké \(i\) a \(j\) neplatilo, vieme vymeniť im zodpovedajúce kódové slová, čím zmenšíme hodnotu sumy \(\sum_{i=1}^m p_i\cdot l_i\). To je však v spore s tým, že priradenie kódovaní bolo optimálne, teda malo túto sumu minimálnu.
Veľmi užitočné bude tiež vedieť, ako si tieto kódové slová reprezentovať. Vhodnou štruktúrou bude písmenkový strom. Uvedomme si, že z každého vrcholu vychádzajú dve hrany – jedna reprezentujúca 0 a jedna reprezentujúca 1. V listoch tohto stromu sú potom jednotlivé znaky, ktoré kódujeme. Takýto strom je užitočný na dve veci. Po prvé nám hovorí, aký kód má príslušný znak – stačí prejsť od koreňa k danému listu a zapisovať si, po akých hranách prechádzam.
Naviac nám tento strom dáva postup, ktorým rozkódovať postupnosť zadaných bitov. Začneme v koreni a vždy sa pohneme po tej hrane, ktorú nám určuje aktuálny bit postupnosti. Ak narazíme na list, tak vypíšeme príslušný znak, ktorý sme práve rozkódovali, a pokračujeme opäť od koreňa.
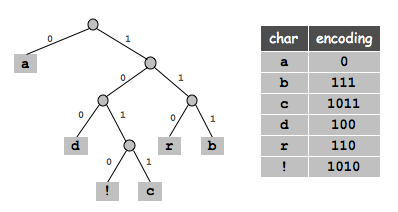
Na záver si ešte uvedomme nasledovné. Každý vnútorný vrchol (teda nelist) tohto stromu má práve dve hrany, ktoré z neho vychádzajú – 0 a 1. Ak by totiž mal iba jedného syna, môžeme tento vrchol odstrániť a nahradiť ho tým jediným vrcholom pod ním. Tým však skrátime kódové slová, čo je v spore s optimálnosťou.
Z toho vyplýva, že slovo \(w_m\) (s dĺžkou \(l_m\)), ktoré je najdlhšie, má suseda, ktorého kód má rovnakú dĺžku a líši sa iba v poslednom bite. Bez ujmy na všeobecnosti, nech je tento sused slovo \(w_{m-1}\) (ak by nebolo, tak ho vymeníme na túto pozíciu a nič tým nepokazíme).
Teraz si už vieme popísať algoritmus, ktorý vytvorí písmenkový strom kódujúci všetky naše znaky a toto kódovanie bude navyše optimálne. Myšlienka je naozaj jednoduchá – zakaždým si zoberieme dva najmenej často sa vyskytujúce znaky. Tie majú mať, podľa našich úvah, najdlhšie kódové slová a navyše majú byť v našom strome susedné. Vytvoríme preto vrchol, z ktorého vychádzajú hrany do dvoch listov, jeden patriaci znaku \(m-1\) a druhý patriaci znaku \(m\). Nemôžeme však na tieto znaky len tak zabudnúť. To čo sa však stalo je, že sme ich zlúčili do jedného spoločného znaku, ktorý je teraz reprezentovaný novovytvoreným vrcholom. A počet výskytov tohto spoločného znaku je predsa \(p_{m-1} + p_m\). Úspešne sme preto zredukovali počet znakov, ktoré potrebujeme ešte spracovať, o jedna. A na to čo nám zostalo môžeme použiť úplne rovnakú myšlienku.
Predstaviť si to môžeme tak, že náš algoritmus má v každom kroku množinu aktívnych vrcholov, ktoré ešte nemajú priradeného žiadneho otca. Každý vrchol má naviac priradenú váhu zodpovedajúcu tomu, ako dôležitý je tento vrchol (ako často sa znaky v listoch pod týmto vrcholom vyskytujú v texte). Na začiatku náš algoritmus začína s \(m\) vrcholmi (listami), každý reprezentuje jeden znak a váha príslušného vrchola je určená podľa počtu výskytov daného znaku v texte.
Následne v každom kroku zoberie dva vrcholy s najmenšou váhou a vytvorí nový vrchol, ktorý bude slúžiť ako otec týchto dvoch vrcholov. Jeho váha bude daná súčtom váh jeho synov. Následne pôvodné dva vrcholy prestane náš algoritmus uvažovať, lebo im už priradil otca. Musí však začať uvažovať novovytvorený vrchol, ktorý otca ešte nemá. V každom kroku sa však zmenší počet vrcholov, ktoré ešte potrebuje spracovať o 1 a preto po \(m-1\) krokoch mu ostane iba jediný vrchol – koreň celého stromu.
Takéto kódovanie sa nazýva Huffmanovo a skutočne je najlepšie možné, ktoré vieme dostať pri daných predpokladoch. Dôkaz optimálnosti som sa rozhodol sem neuviesť, keďže je pomerne formálny (aj keď vôbec nie ťažký). Ak by vás zaujímal, tak si ho môžete pozrieť tu: Úvod do teórie kódovania (3.3.3).
Jeho implementácia je takisto pomerne jednoduchá. Uvedomme si, že nám stačí použiť jednu haldu, v ktorej si udržiavame váhu jednotlivých vrcholov, ktoré ešte potrebujeme spracovať. Z haldy vieme jednoducho vybrať dva vrcholy s najmenšou váhou a spojiť ich. Časová zložitosť takéhoto riešenia bude preto \(O(n \log n)\).
Výsledné riešenie
Vo vzoráku sme si postupne ukázali, ako sa dá programovať v Dávidkovom procesore, ukázali sme si, že pomerne dobré riešenie je zakódovať všetky znaky ako postupnosť bitov, a tú potom postupne dekódovať. Na to sme potrebovali priradiť každému znaku určité kódové slovo a chceli sme aby takéto priradenie vytvorilo čo najkratší kód.
Ukázali sme si, že hľadáme takzvaný prefixový kód (kód ktorý vieme jednoznačne dekódovať) taký, že uprednostňuje častejšie sa vyskytujúce znaky tým, že im priradzuje kratšie kódové slová. Nakoniec sme si ukázali aj konkrétny takýto algoritmus priraďovania – Huffmanov kód.
Ostáva nám už len spojiť všetky tieto veci dokopy a napísať program, ktorý pre daný text vytvorí Huffmanov kód, a následne vypíše program v jazyku Dávidkovho procesora, ktorý bude simulovať rozkódovanie Huffmanovho kódu.
Prekvapivo to však nie je až taký problém. Je nutné si dať pozor na veľa technickejších detailov, mnohé z nich sme však vyriešili v priebehu tohto textu. Najdôležitejšie je dať si pozor, aby ste postupnosť bitov zakódovali do čísel v správnom poradí, a aby ste mali vhodné zarážky – na spodku zásobníka alebo na konci čísla. Navyše, v tomto všeobecnom riešení musí náš program vedieť aj vypočítať, o koľko má skákať dopredu alebo dozadu na príkaze JGZ. Keď si to však trochu premyslíte, mali by ste vedieť tento problém vyriešiť.
A keďže raz vidieť je lepšie ako stokrát počuť, tak vám rovno ukážeme už hotový algoritmus, ktorý úlohu rieši. Odporúčame sa aspoň zbežne pozrieť na časť s Huffmanovým kódovaním.
#include <cstdio>
#include <string>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
using namespace std;
#define For(i,n) for(int i=0; i<(n); i++)
#define mp(a,b) make_pair((a),(b))
typedef pair<int,int> pii;
struct node {
int znak;
int left, right;
node() {
znak = -1;
left = -1; right = -1;
}
};
vector<char> Text;
vector<node> Huff_tree;
vector<string> Kody;
// funkcia prechádza stromom a pamätá si kódy znakov
void prelez(int kde, string kod) {
if(Huff_tree[kde].znak != -1) {
Kody[Huff_tree[kde].znak] = kod;
return;
}
prelez(Huff_tree[kde].left, kod+"0");
prelez(Huff_tree[kde].right, kod+"1");
}
int main() {
// načítam text
char c;
while(scanf("%c",&c) == 1) Text.push_back(c);
// spočítam výskyty jednotlivých znakov
vector<int> Vyskyt; Vyskyt.resize(128,0);
For(i,Text.size()) Vyskyt[Text[i]]++;
// vytvor strom Huffmanovho kódovania
priority_queue<pii> Q;
For(i,128) {
if(Vyskyt[i] == 0) continue;
// vložím do haldy výskyty aktuálneho znaku a spravím preň vrchol v strome
// vkladám záporné hodnoty, aby som mal najmenšie čísla na vrchu haldy
Q.push(mp(-Vyskyt[i], Huff_tree.size()));
Huff_tree.push_back(node());
Huff_tree[Huff_tree.size()-1].znak = i;
}
// spájam dva vrcholy s najmenšou váhou
while(Q.size() != 1) {
pii a=Q.top(); Q.pop();
pii b=Q.top(); Q.pop();
Q.push(mp(a.first+b.first, Huff_tree.size()));
Huff_tree.push_back(node());
Huff_tree[Huff_tree.size()-1].left = a.second;
Huff_tree[Huff_tree.size()-1].right = b.second;
}
// rekurzívnou funkciou prelez() zistím aké kódy som priradil jednotlivým znakom
Kody.resize(128,"");
prelez(Huff_tree.size()-1,"");
// vytvorím si postupnosť bitov, ktoré chcem zakódovať
string tok_bitov = "";
For(i,Text.size()) tok_bitov += Kody[Text[i]];
reverse(tok_bitov.begin(), tok_bitov.end());
// zarážka na spodok zásobníka
printf("PUSH 0\n");
// zakódujem 30 bitov do jedného čísla, ktoré vložím na zásobník
int kolko=0, cislo=1;
For(i, tok_bitov.size()) {
cislo *= 2; cislo += tok_bitov[i]-'0';
kolko++;
if(kolko == 30 || i == tok_bitov.size()-1) {
printf("PUSH %d\n",cislo);
cislo=1; kolko=0;
}
}
// spočítam si, na ktorých riadkoch budú začínať jednotlivé kusy kódu
// pre jednotlivé vrcholy Huffmanovho kódu. Vďaka tomu budem počítať,
// kam sa mám presunúť pri príkaze JGZ
vector<int> Riadky;
Riadky.resize(Huff_tree.size()+1,14);
For(i,Huff_tree.size()) {
// 14 a 5 sú počty príkazov v jednotlivých častiach výsledného kódu (viď nižšie)
if(Huff_tree[i].znak == -1) Riadky[i] = 14;
else Riadky[i] = 5;
}
for(int i=Huff_tree.size()-1; i>=0; i--) Riadky[i]+=Riadky[i+1];
//skontrolujem, či na vrchu zásobníka nie je 0 a nemám už skončiť
printf("PUSH -1\n");
printf("READ\n");
printf("PUSH -1\n");
printf("ADD\n");
printf("PUSH 8\n");
printf("JGZ\n");
printf("MUL\n");
printf("PUSH -1\n");
printf("READ\n");
printf("PUSH 3\n");
printf("JGZ\n");
printf("PUSH 1\n");
printf("PUSH 1000000\n");
printf("JGZ\n");
// Každý vrchol Huffmanovho stromu má priradenú časť programu, ktorá
// spracováva čo sa v ňom má stať. Buď vypísať znak a skočiť na začiatok
// alebo sa rozhodnúť podľa zvyšku po delení 2.
for(int i=Huff_tree.size()-1; i>=0; i--) {
if(Huff_tree[i].znak == -1) {
//časť programu riešiaca vnútorný vrchol stromu
printf("PUSH -1\n");
printf("READ\n");
printf("PUSH -1\n");
printf("ADD\n");
printf("PUSH 1\n");
printf("JGZ\n");
printf("MUL\n");
printf("PUSH 2\n");
printf("DIV\n");
printf("PUSH %d\n",Riadky[Huff_tree[i].right+1]-Riadky[i]+3);
printf("JGZ\n");
printf("PUSH 1\n");
printf("PUSH %d\n",Riadky[Huff_tree[i].left+1]-Riadky[i]);
printf("JGZ\n");
}
else {
//časť programu riešiaca list stromu
printf("PUSH %d\n",Huff_tree[i].znak);
printf("OUT\n");
printf("PUSH 1\n");
printf("PUSH %d\n",-5-Riadky[i+1]);
printf("JGZ\n");
}
}
}Text
3.inpreskakujem úmyselne. Vieme naň síce vymyslieť vcelku jednoduché a pomerne dobré riešenie, nijak však nesúvisí so vzorovým riešením, a preto ho tu nespomeniem.↩
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.