Zadanie
Kedysi dávno existoval raz jeden ľúbostný párik kyklopov. Očakávali štvorčatá. Čo však ale nevedeli je, že pred narodením jedno zo štvorčiat pohltilo ostatné, a narodilo sa iba jedno ,,kyklopiatko’‘. Jediné, čo z ostatných ostalo, boli ich oči, a preživšie obriatko preto pomenovali ,,Štvoročko’‘. Časom sa ukázalo, že ,,pohltenie’‘malo aj iné vedľajšie účinky, a podľa nich premenovali dieťa na ,,Trúba’’. (Čiastočne tiež aj preto, že pôvodné meno nezodpovedalo pohlaviu.)
Dnes je Trúba dospelá, a ako každý správny dospelý jedinec sa každý nedeľný podvečer zamýšľa nad zmyslom života, vesmíru a všetkého. Odpoveď na túto otázku sa snaží nájsť, ako mnohí iní, vo hviezdach. To jej ale prinieslo veľa utrpenia — veľmi ju z toho boleli oči. Odpozorovala, že oči ju bolia práve vtedy, keď sa pozerá súčasne na štvoricu bodov, ktoré netvoria konvexný štvoruholník.
Je presvedčená, že pri takýchto bolestiach odpoveď na veľkú otázku života, vesmíru a všetkého určite nenájde. Preto sa rozhodla, že odpoveď bude hľadať iba v tých častiach oblohy, ktoré sú jej na pohľad príjemné. Pre ľubovoľnú časť oblohy by preto potrebovala zistiť jej príjemnosť.
Úloha
Daná je množina bodov. Zistite, akú časť zo všetkých neusporiadaných štvoríc rôznych bodov tvoria tie, ktoré tvoria konvexný štvoruholník.
Formát vstupu
Na prvom riadku vstupu je \(n\) – počet bodov. V každom z ďalších \(n\) riadkov sú dve čísla \(x_i, y_i\) oddelené medzerou – \(x\)-ová a \(y\)-ová súradnica \(i\)-teho bodu. Každé dva body sú rôzne.
Platí \(|x_i|,|y_i| \leq 10^9\), \(n \leq 10^3\).
Formát výstupu
Na výstup vypíšte zlomok v základnom tvare – podiel počtu štvoríc tvoriacich konvexný štvoruholník a všetkých štvoríc. Pre účely tejto úlohy aj \(0/0\) je zlomok v základnom tvare.
Príklady
Input:
4
-1 -1
0 0
-1 1
1 0Output:
0/1Input:
5
-1 3
2 4
5 5
6 3
7 1Output:
1/5Budeme počítať počet tých štvoríc bodov, ktoré netvoria konvexný štvoruholník. Takúto štvoricu budeme nazývať nekonvexná. Ak počet nekonvexných štvoríc je \(p\), potom odpoveď na zadaný problém je \({n \choose 4} - p\) (kedže všetkých štvoríc bodov je \({n \choose 4}\)).
Zoberme si nekonvexnú štvoricu bodov takú, že jej body neležia všetky na jednej priamke. Potom tejto štvorici vieme prirodzene priradiť stred a tri ramená – stred je ten vrchol spomedzi tej štvorice, ktorý leží vo vnútri trojuholníka tvoreného ostatnými tromi vrcholmi. Ramená sú zvyšné tri vrcholy. V nasledujúcich obrázkoch je stred vyznačený červenou farbou, ramená bielou:
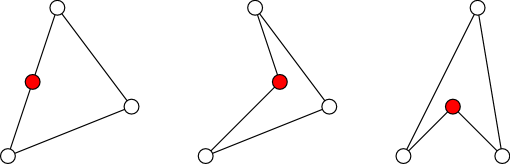
Ak tie štyri body ležia na jednej priamke, tak jej vieme stred a ramená priradiť dvomi spôsobmi.

Všimnime si, že neexistuje priamka vedúca cez stred taká, že všetky tri ramená ležia na jednej strane tejto priamky. Zoberme si teraz nejakého kandidáta na stred \(A\), a troch kandidátov na ramená \(B, C, D\). Potom [\(ABCD\) netvorí konvexný štvoruholník a \(A\) je stredom štvorice \(A, B, C, D\)] platí práve vtedy, keď neexistuje priamka vedúca cez \(A\) taká, že \(B, C\) aj \(D\) sú na jednej strane tejto priamky. (Ak takáto priamka existuje, tak síce \(ABCD\) môže netvoriť konvexný štvoruholník, ale \(A\) už nebude stredom tejto štvorice.)
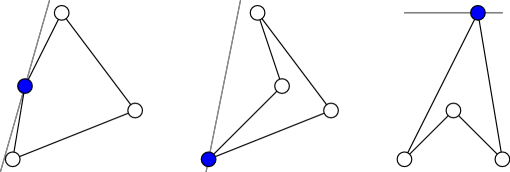
Náš algoritmus bude pracovať nasledovne: vyskúšame každý bod ako stred. Pre aktuálne zvoleného kandidáta na stred \(A\) zistíme, koľko trojíc ostatných bodov spĺňa: neexistuje priamka vedúca cez \(A\) taká, že tie tri body sú na jednej strane od tej priamky. Takto ale zarátame dvakrát štvorice bodov také, že ležia na jednej priamke. Preto ešte odčítame počet takých štvoríc bodov, a dostaneme tak vytúžené \(p\) (počet nekonvexných štvoríc bodov).
Počet štvoríc bodov ležiacich na jednej priamke vieme vypočítať ľahko – pre každý bod \(A\) spočítame, koľko trojíc bodov \(B, C, D\) je takých, že \(A, B, C, D\) ležia na jednej priamke a pritom \(A\) je krajný bod tejto štvorice (teda na priamke ležia v poradí \(A\), a potom ostatné body). Usporiadame si všetky body \(X\) primárne podľa toho, aký orientovaný uhol zviera polpriamka \(\overrightarrow{AX}\) s vodorovnou osou, a sekundárne podľa dĺžky \(|AX|\). Ďalej to zvládnete aj sami…
Zaujímavejšia časť je pre aktuálneho kandidáta na stred \(A\) zistiť počet vyhovujúcich trojíc. Opäť si pomôžeme tým, že budeme namiesto vyhovujúcich trojíc počítať nevyhovujúce – teda trojice bodov \(B, C, D\) také, že existuje priamka \(q\) taká, že \(B, C\) aj \(D\) ležia na jednej strane \(q\).
Všimnime si, že každej vyhovujúcej trojici bodov vieme prirodzene priradiť jeden špecifický bod – ten, ktorý je v smere hodinových ručičiek “prvý”. Nech to je napríklad \(B\). Ten má navyše tú vlastnosť, že priamka \(AB\) (tj. spojnica stredu \(A\) a tohto význačného bodu \(B\)) skoro má požadovanú vlastnosť – \(C\) aj \(D\) ležia na jednej strane od tejto priamky, a \(B\) leží na nej. Nakoľko iba jeden z bodov \(B, C, D\) na nej leží, vieme priamku o máličko otočiť tak, že všetky tri body budú na jednej strane od tej priamky.
V nasledujúcom obrázku je stred označený modrou, “prvý” bod označený zelenou.
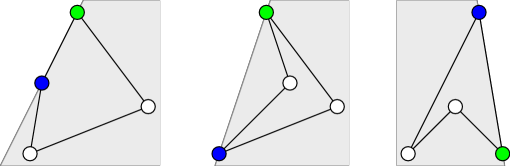
Na základe týchto pozorovaní vieme pre konkrétny stred spočítať počet nevyhovujúcich trojíc nasledovne: najprv utriedime všetky body okrem stredu \(S\) polárne. Následne si zvolíme počiatočného kandidáta \(X\) na “prvý” bod. Potom nájdeme prvý bod v smere hodinových ručičiek taký, že neleží napravo od polpriamky \(\overrightarrow{SX}\). Pritom si počítame, koľko bodov sme vyskúšali – o nich vieme, že sú to všetky body ležiace napravo od \(\overrightarrow{SX}\). Ak ich počet označíme \(k\), vieme, že pre aktuálne zvolený “prvý” bod máme \(k \choose 2\) možností vybrať zvyšné dva body tak, aby ležali napravo od \(\overrightarrow{SX}\).
V nasledujúcom obrázku je stred označený modrou a “prvý” bod zelenou. Prvý bod v smere hodinových ručičiek, ktorý nie je napravo od \(\overrightarrow{SX}\), je čiernou.
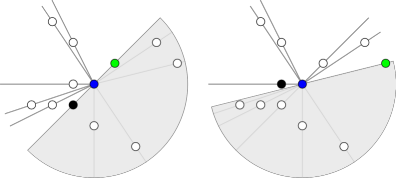
Postupne v smere hodinových ručičiek vyskúšame všetky body ako “prvé”. Pritom si všimneme, že keď “prvý” bod posunieme v smere hodinových ručičiek, tak prvý nevyhovujúci bod sa tiež pohne v smere hodinových ručičiek. A ľahko odtiaľ vidno, že keď vyskúšame všetky body ako “prvé”, prvý nevyhovujúci bod sa posunie najviac toľkokrát, koľko je všetkých bodov.
Nasledujúci obrázok pekne demonštruje tento proces “posúvania”.
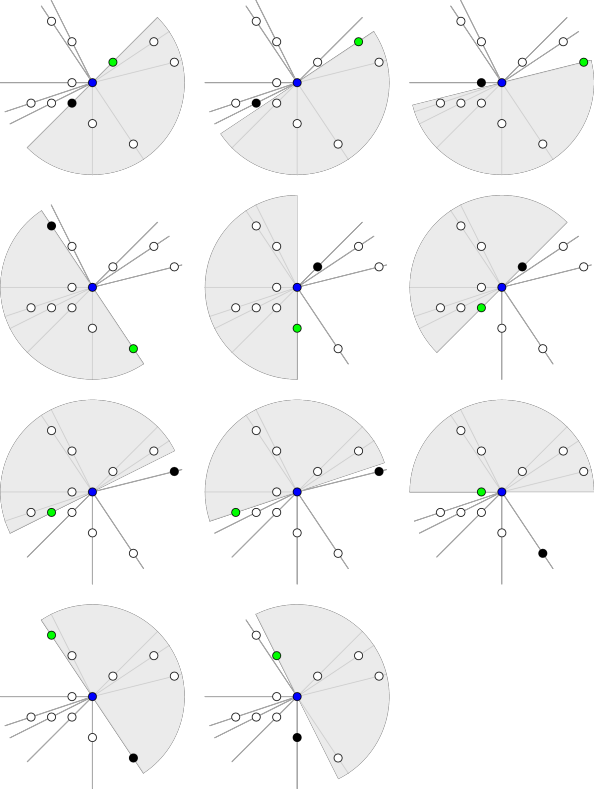
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.