Pred tým, než začnete študovať tento text je dobré sa uistiť, že viete ako funguje prehľadávanie grafu do hĺbky (DFS).

Artikulácie

Nech $G$ je neorientovaný súvislý graf s $n$ vrcholmi a $m$ hranami. Vrchol $v$ nazveme artikulácia, ak sa graf $G-{v}$ (graf bez vrcholu v) skladá z viac ako jedného komponentu.

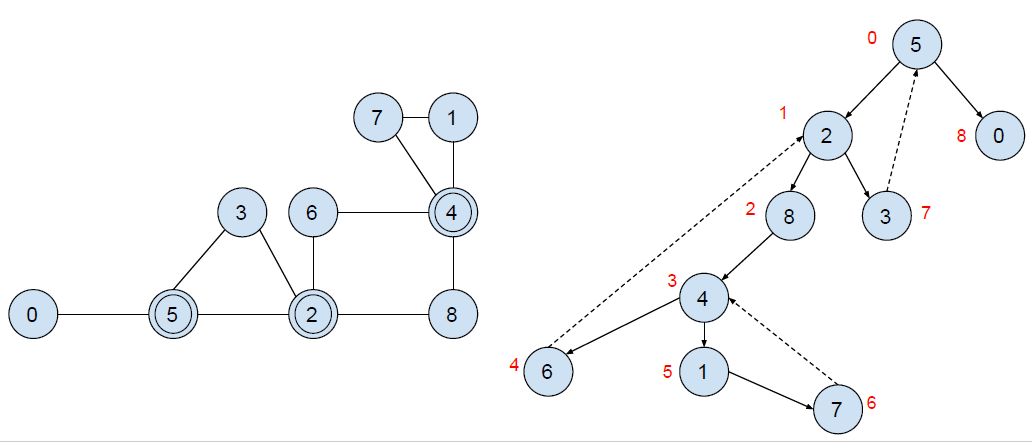
Artikulácie sú teda vrcholy, ktorých odstránenie z grafu spôsobí rozpadnutie tohto grafu na viacero komponentov. Na obrázku hore sú to vrcholy 2, 4 a 5. Otázkou je, ako takého vrcholy nájsť. Samozrejme, jedna možnosť je vyskúšať odstrániť každý vrchol a potom niektorým z prehľadávaní zistiť, či vytvorený graf obsahuje viacero komponentov. Takéto riešenie má však časovú zložitosť $O(n(n+m))$, čo je príliš pomalé.

Pozrieme, ako bude vyzerať prehľadávanie DFS algoritmom. Ten postupne navštevuje vrcholy grafu a postupuje pri tom do hĺbky. DFS navštívi každý vrchol práve raz. Keď si pre každý vrchol zoberieme iba hranu, ktorou doňho DFS algoritmus prišiel dostaneme strom nazývaný aj DFS strom. Zvyšné hrany v grafe objavíme počas prehľadávania ako hrany vedúce už k prehľadávaným susedom. Tieto hrany nazveme stromové. Počas prehľadávania teda narazíme iba na dva typy hrán:

• stromová -- hrana patriaca do DFS stromu, ktorou sme objavili nový vrchol
• spätná -- hrana vedúca do už objaveného vrcholu vyššie v strome

Na obrázku vyššie si môžete prezrieť zakreslenie DFS stromu, ktorý vytvorí algoritmus DFS začínajúci vo vrchole 5. Spätné hrany sú označené prerušovanou šípkou. Začať prehľadávanie môžeme z ľubovoľného vrcholu. Okrem toho, vrcholom priraďujeme nové čísla (označené červenou), ktoré voláme index. Index vrcholom priraďujeme podľa poradia v akom sme ich našli. To znamená, že na ceste z koreňa do ľubovoľného vrcholu indexy vrcholov rastú a spätná hrana vedie vždy do vrcholu s menším indexom (vedie do už skôr objaveného vrcholu).

Ďalej si uvedomme, že ak by sa v našom grafe nenachádzala žiadna spätná hrana, zadaný graf by bol strom a v strome je každý nelistový vrchol artikulácia. To čo zabraňuje vrcholu aby bol artikuláciou sú práve spätné hrany. To si môžeme všimnúť aj na obrázku. Vrchol 8 nie je artikuláciou, lebo ak ho odstránime, medzi vrcholmi 2 a 4 bude stále existovať cesta cez spätnú hranu vedúcu z vrcholu 6 do vrcholu 2.

A práve to je pointa riešenia. Ak po odstránení nejakého vrcholu $x$ zostane celý graf súvislý, tak komponenty ležiace pod $x$ obsahujú spätnú hranu, ktorá ich spája s vrcholom s menším indexom ako má vrchol $x$. Na zisťovanie toho, či takáto hrana existuje si zavedieme nasledovnú hodnotu.

Nazvime Low link vrcholu $v$ ($ll(v)$) najmenšie číslo $a$ také,; že existuje cesta z vrcholu $v$ skladajúca sa z niekoľkých (aj 0) stromových hrán (vedúcich dodola) a práve jednej spätnej hrany, a táto cesta vedie do vrcholu s indexom $a$.

Pomocou hodnoty $ll(v)$ teraz vieme vysloviť dôležitú vetu:

Veta: Nech $v$ je vrchol grafu $G$, ktorý nie je koreň. Potom $v$ je artikulácia práve vtedy ak aspoň pre jedného jeho syna $w$ platí $Index[v] \leq ll(w)$.

Dôkaz: Nech $w$ je syn vrcholu $v$, pre ktorý platí spomenutá podmienka. To znamená, že žiadna spätná hrana z podstromu pod vrcholom $w$ nevedie do vrcholu s menším indexom ako $v$. Ak preto odstránime tento vrchol $v$, nebude existovať žiadne spojenie medzi komponentom v ktorom je $w$ a zvyškom grafu.

Na dokázanie druhej implikácie použijeme nepriamy dôkaz. Nech pre všetkých synov vrcholu $v$ platí $ll(w) < Index[v]$. Potom z každého podstromu pod vrcholom $v$ vedia hrana do komponentu nad vrcholom $v$. Ak preto odstránime vrchol $v$, graf zostane súvislý, preto $v$ nebol artikulácia.

Dôvod, prečo sme toto nemohli tvrdiť o koreni DFS stromu je ten, že nikdy nevieme dosiahnuť menší index ako má koreň tohto stromu -- 0. Uvedomme si však, že koreň je artikulácia práve vtedy, ak má aspoň dva podstromy. Medzi týmito podstromami totiž nevedia žiadna hrana (ak by viedla, tak pri prehľadaní jedného prehľadám aj druhý, a preto by neboli dva rôzne podstromy), preto odstránením koreňa vznikne viacej komponentov. V opačnom prípade odstránime iba list stromu a to zachová súvislosť.

Jediné čo nám zostáva je vedieť vypočítať hodnotu $ll(v)$. To však nie je ťažké, vieme to spraviť v jednom DFS prechode. Z vrcholu $v$ totiž buď zoberieme priamu spätnú hranu, alebo sa vydáme jednou stromovou do nižšieho (už spracovaného) vrcholu $w$. Tam sa nám však neoplatí spraviť nič iné, ako použiť hodnotu $ll(w)$. Ak sa do takéhoto vrcholu vie dostať vrchol $w$, tak sa tam vie dostať aj vrchol $v$. Zo všetkých takýchto možností zoberieme tú najmenšiu.

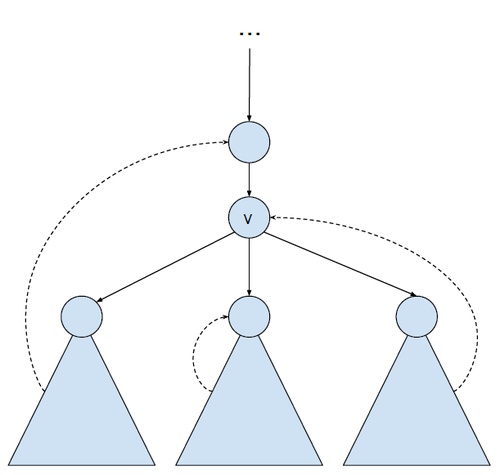
Obrázok ilustruje možnosti pre low linky podstromov. Program naviac ukazuje implementáciu tohto algoritmu. Je treba si dať pozor, že hrana do otca nie je spätná a tiež treba špeciálne ošetriť koreň.

#include <cstdio>
#include <vector>
using namespace std;

vector<vector<int> > G; //zoznam susedov reprezentujici graf
vector<bool> T;         //oznacenie navstivenia
vector<int> Index;
vector<int> LL;         //low link
int n,m;                //pocet vrcholov a hran
int cas=0;

void dfs(int v, int otec) { //vrchol v a jeho otec v strome
    T[v]=true;
    Index[v]=cas++;
    LL[v]=Index[v];
    bool artikulacia=false;
    int pocet_synov=0;
    for(int i=0; i<G[v].size(); i++) {
        int w=G[v][i];
        if(w == otec) continue;
        if(T[w]) {LL[v]=min(LL[v],Index[w]); continue;} //spatna hrana
        pocet_synov++;
        dfs(w,v);         //rekurzive sa zavolam na nenavstiveny vrchol
        LL[v]=min(LL[v],LL[w]);
        if(LL[w]>=Index[v]) artikulacia=true;
    }
    if(otec==-1 && pocet_synov>1) {         //koren
        printf("Vrchol %d je artikulacia\n",v);
    }
    else if(otec!=-1 && artikulacia) {      //nekoren
        printf("Vrchol %d je aritkulacia\n",v);
    }
}

int main() {
    T.resize(n,false);
    Index.resize(n); LL.resize(n);
    //nacitaj graf G
    dfs(0,-1);             //pusti prehladavanie z vrcholu 0
}

Mosty

Podobne ako sme si zadefinovali vrchol, ktorého odstránením znesúvislýme graf, si môžeme zadefinovať aj hranu. Most je taká hrana grafu $G$, že po jej odstránení sa graf rozpadne na viacero komponentov.

Možných riešení, ako nájsť všetky mosty grafu, je viacero. V jednom z nich si doprostred každej hrany vložíme nový vrchol. Následne nájdeme všetky artikulácie a tie nové vrcholy, ktoré sú označené za artikulácie boli vložené do hrán, ktoré boli mostami.

Druhé riešenie je použiť hodnoty $ll(w)$ ktoré používame pri hľadaní artikulácií. Presnejšie, hrana medzi vrcholmi $v$ a $w$ (kde $w$ je v DFS strome synom $v$) je most práve vtedy, ak platí $Index[v]<ll(w)$. (Všimnite si ostrú nerovnosť.) Dôkaz je analogický.