Konvexný obal

Predtým ako sa pustíte do čítania tohto článku, odporúčame najprv si pozrieť Skalárny súčin a vektorový súčin.

Pre ľubovoľnú konečnú množinu bodov v rovine je jednoznačne určený útvar s najmenším obvodom, ktorý ich všetky obsahuje. Je ním ich konvexný obal. (Dôkaz tohto tvrdenia uvádzame nižšie.)

Čo je to konvexný obal?

Útvar $\cal U$ v rovine voláme konvexný, ak má nasledovnú vlastnosť: pre ľubovoľné dva body $A,B\in\cal U$ aj celá úsečka $AB$ patrí do útvaru $\cal U$. Ľudovo povedané, konvexný útvar nemá žiadne diery ani záhyby dovnútra.

Prienik ľubovoľného (dokonca aj nespočítateľne nekonečného!) množstva konvexných útvarov je zjavne opäť konvexný útvar. (Totiž nech $A,B$ sú ľubovoľné dva body z toho prieniku. Potom tieto body sú v každom z pôvodných útvarov. A keďže všetky tie útvary sú konvexné, každý obsahuje celú úsečku $AB$. A teda táto úsečka patrí aj do ich prieniku.)

Konvexný obal danej množiny bodov teda môžeme formálne definovať ako prienik úplne všetkých konvexných útvarov, ktoré danú množinu bodov obsahujú. Menej formálne ale omnoho názornejšie je povedať, že konvexný obal danej množiny bodov je najmenší zo všetkých konvexných útvarov, ktoré danú množinu obsahujú.

A nie je ťažké si uvedomiť, ako tento konvexný obal vyzerá: konvexným obalom danej konečnej množiny bodov v rovine je vždy mnohouholník, ktorého vrcholmi sú niektoré spomedzi zadaných bodov. (Spolu s danými bodmi musí konvexný obal obsahovať aj všetky úsečky spájajúce dva z daných bodov. Tie z úsečiek, ktoré ležia "na obvode", tvoria hranicu hľadaného konvexného mnohouholníka.)

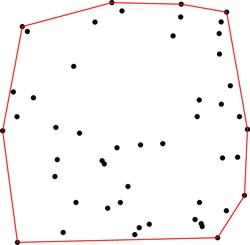
A prečo má teda práve konvexný obal zo všetkých možných útvarov, ktoré našu množinu bodov obsahujú, najmenší obvod?

Intuitívne, predstavme si naše body ako klince a hľadaný útvar ako gumičku natiahnutú okolo nich. Keď gumičku pustíme, tá sa začne sťahovať (a teda skracovať). Najradšej by sa celá skrátila na nulovú dĺžku, to jej ale nedovolia klince v jej vnútri. Časom sa teda ustáli v polohe kedy je najkratšia ako sa dá -- bude napnutá okolo všetkých "vonkajších" klincov. Inými slovami, bude tvoriť práve obvod vyššie popísaného konvexného obalu.

Formálny matematický dôkaz by sa dal spraviť napr. sporom. Nech teda existuje útvar $\cal U$, ktorý obsahuje všetky dané body a má menší obvod ako ich konvexný obal. Zoberme ľubovoľnú stranu $AB$ konvexného obalu, ktorá nie je (celá) súčasťou obvodu útvaru $\cal U$. Predĺžme $AB$ na priamku a označme $A'$ a $B'$ "najľavejší" a "najpravejší" z bodov tejto priamky, ktoré ešte patria do útvaru $\cal U$. (Tieto body vždy existujú, lebo $A$ a $B$ patria do $\cal U$.) Ak ale teraz zahodíme časť obvodu $\cal U$ medzi $A'$ a $B'$ a nahradíme jú úsečkou $A'B'$, dostaneme nový útvar, ktorý tiež obsahuje všetky dané body a má obvod ostro kratší ako $\cal U$. A to je hľadaný spor.

Konštrukcia konvexného obalu

Ukážeme si Grahamov algoritmus, ktorý konvexný obal $n$ bodov zostrojí v čase $\Theta(n \log n)$. Toto je takmer optimálne. (Existujú komplikovanejšie algoritmy s o chlp lepšou časovou zložitosťou $\Theta(n\log h)$, kde $h$ je počet bodov zostrojeného konvexného obalu.)

Začneme tým, že dané body usporiadame zľava doprava a v rámci rovnakej x-ovej súradnice zdola hore. Následne konvexný obal zostrojíme v dvoch prechodoch: v prvom jeho hornú a v druhom jeho dolnú "polovicu". Presnejšie, prvý bod aj posledný bod z usporiadaného poradia (t.j. najspodnejší z najľavejších a najhornejší z najpravejších) určite oba ležia na konvexnom obale a delia ho na dva úseky: "horný" a "dolný". V každom prechode zostrojíme jeden z nich.

Popíšeme prvý prechod, teda zostrojenie horného obalu. (Druhý prechod je potom takmer identický, až na znamienka.)

Budeme postupne spracúvať body v usporiadanom poradí, ktoré sme si pred chvíľou vyrobili. Po spracovaní každého bodu bude platiť, že práve poznáme horný konvexný obal doteraz spracovaných bodov. To je nejaká lomená čiara, ktorá začína v prvom spracovanom bode, niekoľkokrát (možno nulakrát) zatočí doprava a skončí v poslednom spracovanom bode.

Príklad takejto situácie:

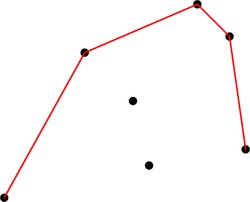
Čo sa teraz stane, keď nám pribudne nasledujúci bod? Body spracúvame usporiadané, nasledujúci bod teda pribudne napravo od doterajšieho konca horného obalu. Najjednoduchšie čo môžeme teraz spraviť je jednoducho obal poň predĺžiť:

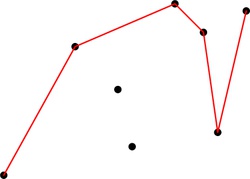
Občas nám však môže nastať práve taká situácia ako na našom obrázku: tým, že sme obal predĺžili, zrazu zatáča do nesprávnej strany a vznikla v ňom "preliačenina". Toto potrebujeme napraviť. Ako? Jednoducho. Problémy vždy nutne spôsobuje práve predposledný bod. Ten sa nachádza na našej lomenej čiare, v skutočnosti však už má ležať pod horným obalom. Z obalu ho preto vyhodíme:

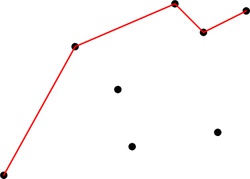
Ale čo to? Aj nasledujúci bod (ktorý je teraz novým predposledným bodom) ešte robí problémy. Aj v ňom chce naša lomená čiara zatáčať doľava, a to nám jednoznačne hovorí, že aj tento bod patrí pod nový horný obal:

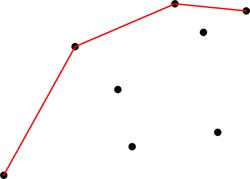
A už je všetko v poriadku a máme hotový horný obal novej množiny bodov.

Akú má toto riešenie časovú zložitosť? Na začiatku potrebujeme usporiadať $n$ bodov, čo spravíme v čase $\Theta(n\log n)$. Následne robíme dva prechody a pri každom vyššie popísaným spôsobom udržiavame časť konvexného obalu. Na prvý pohľad by sa mohlo zdať, že časová zložitosť každého prechodu je kvadratická -- pri pridaní nového bodu môže byť treba veľa nových vyhodiť. Toto sa ale nemôže stávať často. Dobrý pohľad na časovú zložitosť je napr. nasledovný: každý bod na konvexný obal raz pridáme (keď ho spracúvame) a následne ho z obalu nanajvýš raz vyhodíme. Dokopy má celý prechod teda lineárnu časovú zložitosť. (Keďže vždy vyhadzujeme body len z konca zostrojovaného konvexného obalu, stačí si pri implementácii jeho vrcholy pamätať v zásobníku.)