Prvočísla v intervale (Eratostenovo sito)

Prvočíslo je prirodzené číslo, ktoré je väčšie ako 1 a ktorého jedinými deliteľmi sú 1 a ono samo. Prirodzené čísla, ktoré nie sú prvočíslami sa s výnimkou čísla 1 nazývajú zložené čísla. (wikipedia)

Na prvočísla občas natrafíme aj v programátorských úlohách. Často v nich potrebujeme overiť, či je nejaké číslo prvočíslom, prípadne nájsť všetky prvočísla v nejakom intervale (napr. v $[1,10^6]$).

V tomto článku si ukážeme niekoľko jednoduchých spôsobov, ako na to.

Overovanie hľadaním deliteľov

Číslo $n>1$ je teda prvočíslo ak nemá v intervale $[2,n)$ žiadnych deliteľov. Úplne triviálny prístup je teda skúsiť všetky čísla v tomto intervale, a ak žiadne nenájdeme, potvrdíme že je to prvočíslo:

bool je_prvocislo(int n)
{
    for(int i=2;i<n;i++)
    {
        if(n % i == 0)
            return false;
    }
    return n>1;
}

V prípade, že je $n$ prvočíslo, však spravíme až $n-2 = O(n)$ krokov. Toto je príliš pomalé pre $n$ rádovo $10^9$, alebo viacero $n$ okolo $10^6$.

Tu prichádza na rad prvé dôležité pozorovanie. Povedzme, že $n$ nie je prvočíslo. Potom vieme $n$ zapísať ako $n = a \cdot b$, kde (BUNV $a \leq b$) platí $a \leq \sqrt n$. Ak by totiž $b \geq a > \sqrt n$, tak $a \cdot b > n$.

Inak sa na to dá pozerať aj tak, že každý deliteľ väčší rovný $\sqrt n$ má svoju dvojicu, ktorá je menšia rovná ako $\sqrt n $ (a naopak).

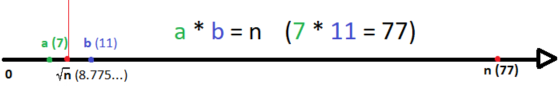
Ak teda nenájdeme deliteľa čísla $n$ v intervale $[2, \sqrt n ]$, nemusíme ďalej hľadať - určite ho nemá ani v intervale $(\sqrt n ,n)$. Úplne jednoducho teda zrýchlime našu funkciu na overovanie prvočíslenosti - budeme hľadať len po odmocninu $n$.

bool je_prvocislo(int n)
{
    for(int i=2;i*i<=n;i++)
    {
        if(n % i == 0)
            return false;
    }
    return n>1;
}

V najhoršiom prípade teda spravíme $O(\sqrt n)$ operácií, ak je číslo prvočíslo alebo súčinom dvoch čísel blízko jeho odmocnine. To je slušné vylepšenie (z obrázku môžete vidieť, o koľko menej čísel overíme už pre relatívne malé $n = 77$); ak by sme takto skúsili overiť všetky čísla od $1$ po $n$ v snahe nájsť všetky prvočísla, zabralo by nám to $O(n \sqrt n) = O(n^{3/2})$ času. V praxi toto môže s rýchlym programovacím jazykom stačiť pre $n$ rádovo $10^6$.

Nasleduje tvrdenie, ktoré uvedemie bez dôkazu (je nad rámec tohto článku): dobrý odhad počtu prvočísel $\leq n$ je $\frac{n}{\log n}$, kde $\log$ označuje prirodzený logaritmus (so základom e ). Počet prvočísel $\leq n$ sa v matematike často označuje $\pi(n)$; toto budeme používať aj v našom článku, pričom $\pi(n) = O(\frac{n}{\log n})$.

Ďalšie vylepšenie môžeme teda spraviť pozorovaním, že ak $n$ je zložené číslo a teda má deliteľov, tak má zaručene aj prvočíselných deliteľov - nemusíme teda skúšať všetky čísla $\leq \sqrt n$, ale len všetky prvočísla $\leq \sqrt n$, ktorých je $\pi (\sqrt n)$. Samozrejme, toto urýchlenie overovania jednotlivých čísel prichádza s cenou - musíme si najprv predpočítať všetky dostatočne malé prvočísla. Toto sa oplatí, ak budeme chcieť overovať viacero čísel, alebo ak našim cieľom nájsť všetky prvočísla do $n$ - vtedy to sú predsa dve muchy jednou ranou.

vector<int> prvocisla;

void najdi_prvocisla(int n)
{
    for(int i=2;i<=n;i++)
    {
    bool ok = true;
        for(int j=0;j<prvocisla.size() && prvocisla[j]*prvocisla[j] <= i;++j)
        {
            if(i % prvocisla[j] == 0)
            {
                ok = false;
                break;
            }
        }

        if(ok)
        {
            prvocisla.push_back(i);
        }
    }
}

Tento prístup má teda časovú zložitosť $O(\frac{n \sqrt n}{\log \sqrt n})$, a pamäťovú $O(\frac{n}{\log n})$.

Eratostenovo sito

A teraz dôvod, prečo ste asi klikli na tento článok - Eratostenovo sito (anglicky sieve of Eratosthenes). Tento algoritmus ide na problém opačne - namiesto toho, aby sme každému číslu $\leq n$ skúsili nájsť dostatočne malého prvočíselného deliteľa, každým prvočíslom prejdeme všetky jeho dostatočne veľké násobky a označíme ich ako zložené. A čo znamená 'dostatočne veľké'? Z vyššie uvedeného pozorovania, že každé číslo má deliteľa menšieho rovného jeho odmocnine vyplýva aj to, že keď už sme správne označili za zložené všetky čísla s prvočíselnými deliteľmi $< k$ pre nejaké $k$, tak každé číslo $< k^2$ už je správne označené - každé číslo $m$ deliteľné $k$ sa predsa dá zapísať ako $m = a \cdot k$; ak je $m < k \cdot k$, tak $a < k$, teda $m$ má (aj prvočíselného) deliteľa menšieho ako $k$: $a$. A my sme usúdili, že všetky čísla s prvočíselnými deliteľmi $< k$ sme už správne označili, a teda aj toto ľubovoľné číslo $m$. Prvočíslom $k$ stačí teda označovať len čísla $ \geq k^2$.

Začneme teda s poľom veľkosti $n+1$ (len kvôli príjemnejšiemu indexovaniu), v ktorom si budeme udržiavať na indexe $k$ informáciu, či sme číslu $k$ našli prvočíselného deliteľa (a teda či je zložené).

Na začiatku sú všetky čísla kandidátmi na prvočíslo, okrem jednotky (kandidáti zelenou, neprvočísla červenou):

Pozrieme sa na prvého kandidáta na prvočíslo: 2. Na indexe 2 máme označené, že sme tomuto číslu deliteľa nenašli. Označíme ju ako prvočíslo (a môžeme s ňou spraviť čo chceme - napríklad ju pridáme do zoznamu prvočísel).

Teraz budeme chcieť označiť všetky jej násobky $\geq 2^2 = 4$ ako zložené čísla. Pôjdeme teda v cykle začínajúc k = 4, označíme 4 za zložené číslo, a presunieme sa na ďalší násobok; práve sme boli na 2x 2, chceme ísť na 3x2 - teda pripočítame k indexu 2: k += 2, dostávame sa na k = 6, označíme ju za zložené číslo, prejdeme na k = 8, potom k = 10...

Presunieme sa na ďalšieho kandidáta: 3. Aj 3 o sebe tvrdí, že sme jej deliteľa nenašli. Je to teda prvočíslo, a ideme označiť všetky násobky $\geq 3^2 = 9$. Označíme 9,12,15,18,21,24.... Dostaneme sa na niektoré čísla ktoré sme už označili dvojkou - nič si z toho nerobíme, a ani to nemusíme nijak ošetrovať. Všade zapíšeme číslu, že je zložené, a ak tomu bolo tak aj predtým, nič sme tým nepokazili.

Ďalší kandidát je 4. Tá má však zapísané, že je zložená, a teda s ňou nič nerobíme a presúvame sa na ďalšieho kandidáta, 5. 5 je veselé prvočíslo, a tak označíme všetky jeho násobky $\geq 25$ za zložené.

A takto pokračujeme ďalej pre všetkých kandidátov $\leq n$. Ak by $n = 26$ ako na našom obrázku, už by sme pre žiadne ďalšie prvočísla nič neoznačili, keďže už sú väčšie ako $\sqrt n$.

Za zmienku stojí to, že teraz vieme jednoducho v $O(1)$ zistiť či je číslo $\leq n$ prvočíslom - pozrieme sa do nášho poľa, v ktorom sme si označovali zložené čísla. Ak je zadané číslo označené, tak nie je prvočíslom, inak ním je.

Nasleduje zodpovedajúci kód:

vector<int> prvocisla;

void Eratosten(int n)
{
    vector<bool> zlozene(n+1,false);
    zlozene[0] = zlozene[1] = true;
    for(long long i=2;i<=n;i++)
    {
        if(zlozene[i])
            continue;

        prvocisla.push_back(i);

        for(long long k = i*i;k<=n;k+=i)
            zlozene[k] = true;
    }
}

Pamäťová zložitosť Eratostenovho sita na nájdenie všetkých prvočísel v $[1,n]$ je $O(n)$ - potrebujeme si pre každé číslo pamätať, či sme mu našli deliteľa alebo nie^[V princípe vieme Eratostena implementovať aj s lepšou pamäťovou zložitosťou, napr. $O(\sqrt n$), bez výrazného zhoršenia času. Ak sa však ocitnete v situácií, kde nevládzete alokovať $O(n)$ pamäte naraz, je dosť možné že chcete siahnuť po sofistikovanejšom algoritme].

Časová zložitosť? Pre každé zložené číslo vykonáme $O(1)$ práce (ignorujeme ho), pre každé prvočíslo $p \leq \sqrt n$ prejdeme $\frac{n-p^2}{p}$ jeho násobkov a označíme ich za zložené. Horný odhad je teda $n + \frac{n}{2} + \frac{n}{3} + \frac{n}{5} + \cdots + \frac{n}{\sqrt n} = n + n(\frac{1}{2} + \frac{1}{3} + \frac{1}{5} + \cdots + \frac{1}{\sqrt n})$. Súčet v zátvorke sa nazýva Harmonic Series of Primes; jeho asymptotický súčet pre prvočísla do $n$ je $O(\log \log n)$, a teda naša časová zložitosť je $O(n + n \log \log n) = O(n \log \log n)$ (dôkaz je opäť nad rámec článku). Pre predstavu, pre $n = 10^6$ spraví náš algoritmus $3\,122\,047$ operácií (prejdenie kandidátov a označenie násobkov), pre $n = 10^8$ už $342\,570\,203$ - v prvom prípade $3.122n$, v druhom, pre sto krát väčšie $n$, $3.426n$. Faktor $\log \log n$ rastie tak pomaly, že skoro bez výnimky sa pre rozmedzia $n$ v súťažných úlohách správa ako konštanta $\leq 4$, a teda keď sa nehráme na teoretikov a trošku prižmúrime oko, beží prakticky v lineárnom čase.

Prvočísla vo vzdialenom intervale

Občas potrebujeme nájsť prvočísla v intervale inom ako $[1,n]$, napríklad $[L,R]$. Ak je $R$ veľké (~$10^9$), horeuvedený postup zlyhá, keďže nájsť prvočísla v $[1,R]$ nám zaberie $O(R \log \log R)$ času. Avšak ak je $L$ blízko $R$, vieme sa s tým vysporiadať technikou nazývanou Segmented sieve of Erathostenes. Tá je založená na tom, že na vylúčenie všetkých zložených čísel ich musíme overiť len prvočíslami menšími rovnými ich odmocnine. Ňou dokážeme nájsť všetky prvočísla v intervale $[L,R]$ v pamäti $O(\sqrt R + R-L)$ a čase $O(\sqrt R \log \log \sqrt R + (R-L)\log \log (R-L) )$.

Prvý krok je jednoduchý - použijeme obyčajné Eratostenovo sito na nájdenie prvočísel v $[1,\sqrt R]$. Následne si vytvoríme pole S (to je náš segment) veľkosti $R-L+1$, kde S[i] reprezentuje číslo $L+i$. Teraz prejdeme všetky prvočísla nájdené prvotným Eratostenom, a každým z nich označíme jeho násobky ktoré sa nachádzajú v našom intervale.

Pre prvočíslo $p$ je prvý jeho relevantný násobok v intervale $[L,R]$ na pozícií $max(\lceil \frac{L}{p} \rceil \cdot p,p^2)$. Následne pooznačujeme všetky jeho násobky na indexoch zodpovedajúcim číslam $\leq R$.

vector<long long> velke_prvocisla;

void Segmented_Eratosten(long long L,long long R)
{
    //nacita do 'prvocisla' vsetky prvocisla po odmocninu z R
    Eratosten(sqrt(R)); 
    vector<bool> zlozene(R-L+1,false);
    if(L==1) zlozene[0] = true;

    for(int i=0;i<prvocisla.size();++i)
    {
        long long p = prvocisla[i];
        long long index = max(p*p,(long long)ceil((double)L/p)*p);
        while(index <= R)
        {
            zlozene[index-L] = true;
            index += p;
        }
    }

    for(int i=0;i<=R-L;++i)
    {
        if(zlozene[i] == false)
        {
            velke_prvocisla.push_back(i+L);
        }
    }
}

Rozklad na prvocisela cez sito

TODO ak si nebudeme do sita pisat true/false ale cislo pocas ktoreho sme sem zapisali false (najmensi prvociselny delitel), tak vieme ziskat uplny prvocisleny rozklad