Kristína si ráno čítala maily a našla tam pozvánku na nejaký výlet od Marcela. Nakoľko len pred chvíľou vstala, bez menšieho zaváhania otvorila prihlášku a začala vypĺňať. Keď už bola na konci, narazila na najťažšiu otázku: “Ako dlhá by mala byť trasa výletu?”. Kike sa z rána veľmi nechcelo rozmýšľať, tak rovno napísala “Ja nevieeem”.
Keď si Marcel pozeral prihlášky a zbadal túto odpoveď, hneď mu bolo jasné, čo musí spraviť. Musí pripraviť vhodnú trasu na každú dĺžku. Ak by nejaká dĺžka chýbala, Kika by si vybrala presne tú a celý deň by sa sťažovala (čo ale teda neznamená, že to nebude robiť aj tak).
Marcel teda naplánoval perfektné trasy všetkých dĺžok. Začiatok majú všetky spoločný, no koncov je už niekoľko. Nakreslil si aj mapku, vyznačil začiatok, cieľové body, rázcestia a teraz mu ostáva už len označiť odbočky pri rázcestníkoch. Nebude to však také ľahké. Marcel by chcel, aby všetky trasy mohol popísať jedným slovom, nech si to Kika zapamätá!
Presnejšie musí platiť nasledovné:
- Slovo popisujúce trasy má rovnakú dĺžku ako najdlhšia trasa.
- Trasu dĺžky \(k\) nájdeme nasledovaním posledných \(k\) písmen slova.
- Z každého rázcestia vychádza niekoľko ciest označených rôznymi písmenami.
- V každom cieľovom bode končí aspoň jedna trasa.
- Každá trasa končí v nejakom ceľovom bode.
Napríklad, ak je slovo abbab, tak trasy, ktoré končia v
cieli nájdeme, iba ak budeme nasledovať slová abbab,
bbab, bab, ab, b
alebo ostaneme v začiatočnom vrchole (pre prípad, že by sa Kike vôbec
nechcelo chodiť).
Úloha
Na vstupe dostanete orientovaný graf a zoznam cieľových vrcholov.
Vašou úlohou je doplniť ku hranám písmená tak, aby graf spĺňal Marcelove podmienky pre nejaké slovo \(w\) a nájsť nejaké takéto slovo.
Pre jednoduchosť budeme namiesto písmen používať celé čísla od \(1\) do \(k\), pričom jediná podmienka je, že \(k \le m\). Môžete tiež predpokladať, že graf, ktorý dostanete sa dá označiť tak, aby Marcelove podmienky spĺňal.
Formát vstupu
Na prvom riadku dostanete tri celé čísla - počet vrcholov \(n\), počet orientovaných hrán \(m\) a počet cieľových vrcholov \(t\) (\(1 \le t \le n\)).
V druhom riadku dostanete \(t\) celých čísel – cieľové vrcholy.
Nakoniec nasleduje \(m\) riadkov, popisujúcich hrany v grafe. Na každom riadku sú dve medzerou oddelené čísla \(s_i\) a \(t_i\), označujúce hranu z vrcholu \(s_i\) do vrcholu \(t_i\). Vrcholy sú označené číslami od \(1\) do \(n\), pričom vrchol \(1\) je vždy začiatočný.
Úloha má 4 sady, pre ktoré platia nasledujúce obmedzenia:
| Sada | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(1 \leq n \leq\) | \(60\) | \(6 \cdot 10^3\) | \(2 \cdot 10^5\) | \(3 \cdot 10^5\) |
| \(1 \leq m \leq\) | \(60\) | \(6 \cdot 10^3\) | \(2 \cdot 10^5\) | \(3 \cdot 10^5\) |
| \(1 \leq t \leq\) | \(60\) | \(3 \cdot 10^2\) | \(5 \cdot 10^2\) | \(8 \cdot 10^2\) |
Formát výstupu
Na prvý riadok výstupu vypíšte dve čísla \(l\) a \(k\) - dĺžka slova \(w\) a počet rôznych čísel na hranách. Na druhý riadok vypíšte slovo \(w\) ako \(l\) celých čísel medzi \(1\) a \(k\) oddelených medzerami.
Na tretí riadok vypíšte \(m\) čísel – označenia hrán v poradí, v akom sú na vstupe tak, aby graf spĺňal Marcelove podmienky.
Príklad
Input:
7 8 4
1 3 4 7
1 2
1 3
2 4
3 5
3 6
4 5
5 6
6 7Output:
5 2
1 2 2 1 2
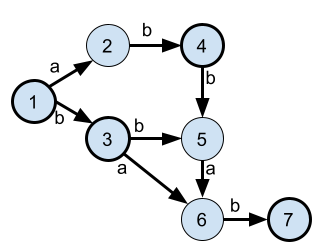
1 2 2 2 1 2 1 2Riešenie je zobrazené na obrázku kde \(1\) predstavuje a a \(2\) b
Odovzdávanie
Na odovzdávanie sa musíš prihlásiť
Otázky a diskusia
Po skončení kola budete mať príležitosť na diskutovanie o riešeniach v diskusii pod vzorovým riešením.