V Krajine Školských Povinností (KŠP) sa zaviedol nový sviatok, takzvaný “opposite day” – opačný deň – v ktorý by sa všetko malo robiť naopak.
Študenti Feľmi Kvalitnej Školy (FKŠ) sa zhodli, že to teda nesmú prísť do školy. Ľahké splniť, všakže?
Na FKŠ však existuje populárny poobedňajší krúžok – Kamaráti Musia Športovať (KMŠ) – ktorí zhrozene pozerajú do rozvrhu na vymeškané športové popoludnie.
Rozhodli sa tak, že všetci členovia krúžku niekam predsalen prísť musia, za účelom udržania kondičky.
Otázka je, kam?
Úloha
Mesto v ktorom sídli FKŠ si vieme reprezentovať budovami, v ktorých bývajú študenti, a cestami ktoré ich prepájajú. Mesto bolo navrhnuté tak, že sa z každej budovy dá cestami dostať do každej inej práve jedným spôsobom.
V každej bytovke býva nezáporné množstvo členov KMŠ, a každá cesta má nejakú kladnú dĺžku v metroch.
Daný je takýto popis mesta, a je určené ktorá z budov je FKŠ.
Športový výkon si zadefinujeme ako súčet dĺžok trás, ktorú prejdú členovia KMŠ aby prišli k zvolenej budove.
Zvyčajne by sa snažilo KMŠ o najväčší športový výkon, keďže je však opposite day, budú sa snažiť o výkon čo najmenší…
Ktorú budovu si majú zvoliť ako stretávacie miesto, aby toto dosiahli?
Formát vstupu
V prvom riadku vstupu sú čísla \(n\) a \(f\): počet budov v meste a číslo budovy FKŠ.
V druhom riadku je \(n\) čísel \(k_i\): počet členov KMŠ, ktorí bývajú v budove \(i\)1.
V každom z nasledujúcich \(n-1\) riadkov sú čísla \(a_i\ b_i\ d_i\), znázorňujúce cestu medzi budovami \(a_i\) a \(b_i\) dlhú \(d_i\) metrov. Budovy sú očíslované od \(1\) po \(n\).
Je zaručené, že sa z každej budovy dá dostať ku každej inej budove.
Formát výstupu
Vypíšte číslo budovy, rôzne od \(f\), ku ktorej je súčet dĺžok trás všetkých členov KMŠ najmenší. Ak je takýchto budov viac, vypíšte tú s najmenším číslom.
Obmedzenia
Platí \(2 \leq n \leq 100,000\) a \(1 \leq f \leq n\).
\(0 \leq k_i \leq 10^4\).
\(1 \leq a_i \neq b_i \leq n\) a \(1 \leq d_i \leq 10^4\).
Sú štyri sady vstupov.
V prvej navyše platí \(n \leq 1\,000\).
V druhej zasa platí že \(a_i, b_i = i, i+1\) – teda celé mesto leží na čiare.
Príklady
Input:
4 1
1 2 3 4
1 2 7
2 3 6
3 4 5Output:
3Tento vstup je príkladom z druhej sady. Športové výkony ktoré by KMŠ podalo pre danú vybratú budovu sú postupne 125, 69, 45, 55. Pre budovu 3 je športový výkon najmenší, tak si vyberú ju. Jej športový výkon je 45, pretože KMŠák z budovy 1 prejde trasu 13, z budovy 2 prejdú dvaja študenti trasu 6, KMŠáci v tretej budove zídu na prízemie výťahom, a zo štvrtej budovy prídu štyria KMŠáci cestou dĺžky 5. Dokopy teda KMŠ podalo výkon \(1*13 + 2*6 + 3*0 + 4*5 = 45\).

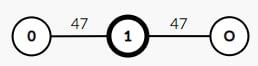
Input:
3 2
0 1 0
1 2 47
3 2 47Output:
1Vedúci KMŠ by radšej zostal vo FKŠ, je však opačný deň, tak ku FKŠ prísť nemôže. Pre obe iné budovy by jeho športový výkon bol 47, tak si vyberie tú s menším číslom.
Input:
6 4
5 8 2 3 1 4
4 5 3
5 6 8
1 3 1
2 5 1
3 6 9Output:
5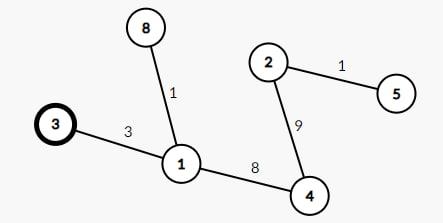
Áno, niektorí študenti sú premotivovaní, a bývajú v škole. To preto, že je feľmi kvalitná.↩︎
Odovzdávanie
Na odovzdávanie sa musíš prihlásiť
Otázky a diskusia
Po skončení kola budete mať príležitosť na diskutovanie o riešeniach v diskusii pod vzorovým riešením.