6. Totálna pohroma

Syseľ sa s hlbokým výdychom zvalil na svoju kancelársku stoličku. Hotovo! Po mesiacoch úpornej driny sa mu konečne podarilo dokončiť samofunkčný vysávač poháňaný jadrovým reaktorom. Jediný vysávač takéhoto druhu na celom svete. Proste unikát.

Bol položený na stole pred ním, chrómované telo odrážalo svetlo, trubica vedúca zo stredu sa pomaly otáčala a snažila sa nájsť špinu na vysatie, to všetko doplnené jemným bzukotom reaktora. A všade naokolo papiere, nákresy, výpočty, kusy kódu. Naprogramovať umelú inteligenciu bola pre Sysľa hračka, konštrukcia vysávača tiež nebola problematická. Reaktor mu však dal zabrať. Ani by ste netušili, aký je problém zohnať dostatočné množstvo kvalitného uránu. Ale ani keď ho len tak hodíte do vnútra, tak to nezačne fungovať. Lietajúce neutróny treba celý čas precízne kontrolovať, jednak aby jadrová reakcia nevyhasla, jednak aby to celé nevybuchlo.

Tajomstvom je použitie špeciálnej kontrolnej matice rozmerov \(n \times n\), cez ktorú neutróny filtrujete. Každé políčko je buď priepustné alebo nepriepustné, je však dôležité, aby platilo, že v každom štvorci okolo hlavnej diagonály je práve párny počet nepriepustných políčok. Presnejšie, ak si ľavý horný roh matice označíte súradnicami \((1, 1)\) a pravý dolný súradnicami \((n, n)\), tak musí platiť, že každý štvorec, ktorého protiľahlé rohy sú na súradniciach \((i, i)\) a \((j, j)\) (pre \(i < j\)) má párne veľa nepriepustných políčok. Syseľ pohľadom zavadil o nákres tejto kontrolnej matice, ktorý ležal pred ním na stole. Asi by ho mal niekam odložiť, predsa je to len najdôležitejšia časť jeho výtvoru a on si ju ešte nestihol zálohovať.

V tom však do miestnosti vstúpila ona a Syseľ zabudol na všetko ostatné. Nikol. Najlepšia programátorka v celom VacuumLabs. Keby ste ju videli ako píše na svojej ergonomickej klávesnici. Prsty sa jej len tak mihajú po klávesách. A keď potom spraví pull request, pozerať sa naňho chodia ešte aj z Exponei. K tomu všetkému je ešte aj nesmierne krásna a nezadaná. Len nedávno sa síce rozišla so svojím priateľom¹, ale je najvyšší čas, aby Syseľ spravil prvý krok. A jadrový vysávač môže byť presne tá vec, ktorá ju ohúri.

Keď Nikol vošla do miestnosti, Syseľ sa v okamžiku postavil zo stoličky, aby ju privítal. Pritom však na stôl vysypal omrvinky z keksíkov, ktoré jedol počas práce. Jeho inteligentný vysávač to hneď zaregistroval a začal otáčať trubicu aby ich vysal. Pritom však omylom prevrhol pohár vody a tá sa rozliala po nákrese kontrolnej matice. Katastrofa! Ako teraz Syseľ ohúri Nikol, keď je jeho výtvor zničený? Na mokrom papieri je vidno už iba niekoľko 0 a 1, ktoré predstavujú priepustné a nepriepustné políčka. Pomôžte Sysľovi zistiť, koľkými spôsobmi vie doplniť zvyšok matice, nech sa môže pustiť do opravovania.

Úloha

Na vstupe dostanete veľkosť matice \(n\) a políčka, ktoré ostali zachované spolu s ich pôvodnými hodnotami – 0 alebo 1. Zistite, koľkými spôsobmi je možné doplniť zvyšné políčka tejto matice číslami 0 a 1 tak, aby platilo, že v každom štvorci okolo hlavnej diagonály so stranou väčšou ako 1 je párne veľa jednotiek.

Hlavná diagonála matice je tvorená políčkami, pre ktoré platí, že ich \(x\)-ová a \(y\)-ová súradnica je rovnaká. Ťahá sa preto od ľavého horného rohu (súradnice \((1, 1)\)) k pravému dolnému rohu (súradnice \((n, n)\)). Štvorec je okolo hlavnej diagonály vtedy, ak dva jeho protiľahlé rohy ležia na hlavnej diagonále.

Keďže počet spôsobov, ako doplniť maticu, môže byť naozaj veľký, vypíšte iba ich zvyšok po delení číslom \(1\,000\,000\,009\).

Formát vstupu

Na prvom riadku vstupu sa nachádzajú dve celé čísla \(n\) a \(m\) (\(2 \leq n \leq 10^5\), \(0 \leq m \leq min(50\,000, n^2)\)) – veľkosť matice a počet zachovaných políčok.

Nasleduje \(m\) riadkov, každý popisuje jedno zachované políčko pomocou troch čísel \(x_i\), \(y_i\) a \(c_i\) (\(1 \leq x_i, y_i \leq n\), \(0 \leq c_i \leq 1\)) – súradnice tohto políčka a jeho hodnota. Je zaručené, že jedno políčko sa môže objaviť na najviac jednom riadku vstupu.

Testovacie vstupy pre túto úlohu sú rozdelené do 8 sád, pre ktoré platia nasledovné dodatočné obmedzenia:

• V sade 1 platí, že \(n = m\) a všetky zadané políčka ležia na hlavnej diagonále. Inými slovami, máte presne zadané ako vyzerá hlavná diagonála a nič naviac.
• V sade 2 a 3 platí, že \(n \leq m\) a medzi zadanými políčkami sa vyskytujú všetky políčka na hlavnej diagonále. Oproti vstupm zo sady 1 teda máte aj zadaných aj niekoľko dodatočných políčok.
• V sade 4 platí, že \(n \leq 20\).
• V zvyšných sadách neplatia žiadne dodatočné obmedzenia.

Formát výstupu

Na výstup vypíšte jedno celé číslo – počet možností, ktorými je možné doplniť maticu \(n \times n\) číslami 0 a 1 tak, aby platila zadaná podmienka. Toto číslo vypíšte modulo \(1\,000\,000\,009\).

Príklad

Input:

3 3
1 3 1
3 2 0
1 1 1

Output:

8

Všetky možné doplnenia sú uvedené na nasledovnom obrázku:

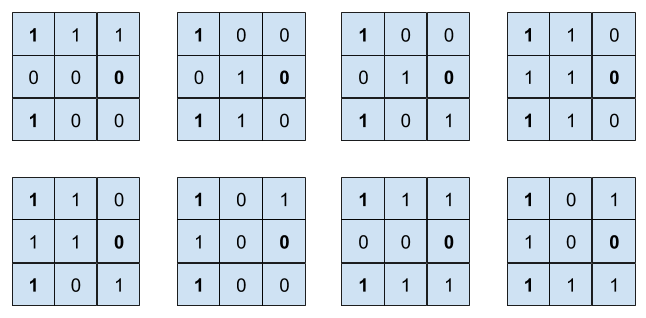
Input:

3 6
1 1 1
1 2 1
2 1 1
3 3 0
3 2 0
2 3 0

Output:

0

Ak do stredného políčka dopíšeme 0, štvorec \(2\times 2\) v ľavom hornom rohu nebude mať párne veľa jednotiek. A ak do stredného políčka dopíšeme 1, zlý bude pravý dolný \(2 \times 2\) štvorec.