Píše sa rok \(2143\). Presne pred \(100\) rokmi sa človek stal multiplanetárnym druhom, keď prví vesmírni osadníci pristáli na Marse a následne vybudovali kolóniu. Na začiatku ich tam bolo presne \(157\) a každý tak mal dostatok priestoru, keďže pôvodná kapacita prvej kolónie sa šplhala až k číslu \(1223\).
Časom však populácia červenej planéty rástla1. \(53\%\) terajších obyvateľov pricestovalo zo Zeme alebo z Mesiaca a \(47\%\) sa na Marse už narodilo. Preto už takýchto kolónií existuje niekoľko (rádovo v stovkách). Čoskoro, teda, dôjde k vyrovnaniu pomeru úplných2 a polovičných3 “Marťanov”, a veľkosť populácie prekročí \(200\,000\).
Znie to veľmi sľubne a prosperujúco, no obyvateľov Marsu stále ešte obmedzuje pár vecí, medzi ktoré patrí napríklad aj doprava. Na prepravu materiálu, potravín alebo osôb sa v tomto nehostinnom teréne používajú elektrické rovery. Tie majú svoje nevýhody: sú pomalé, často sa kvôli prašnému povrchu kazia, majú relatívne malú nosnosť a, samozrejme, z bezpečnostných dôvodov nepremávajú počas Marťanskej búrky. Preto sa Rada kolónií Marsu, Aliancia štátov pre multiplanetárny život a Medzinárodná rada vesmírnych agentúr rozhodli riešiť dopravu na tejto planéte.
Za najvhodnejší spôsob prepravy osôb a tovaru tu považujú vlaky, premávajúce hermeticky uzavretými podzemnými tunelmi. Tie budú môcť premávať aj počas búrok4, uvezú veľa nákladu, nebudú vystavené prašnému prostrediu a budú relatívne rýchle5. Okrem toho, odhlasovalo sa, že z bezpečnostných dôvodov6 budú všetky tunely vybudované v rovnakej hĺbke, a to znamená, že žiadne dva tunely sa nesmú križovať. V každom tuneli bude premávať práve jeden vlak. Vlaky sú totiž najdrahšou položkou v tomto projekte a preto ich počet, a teda aj počet tunelov, bude čo najnižší. Zároveň ich treba toľko, aby sa bolo možné dostať z ľubovoľnej kolónie do hociktorej inej len použitím vlakov. Ak si teda vlakovú sieť predstavíme ako graf, tak bude vyzerať ako strom, z čoho vyplýva, že počet tunelov bude počet kolónií mínus \(1\).
Plán projektu sa skladal z troch tabuliek:
- V jednej boli spárované identifikačné čísla pozícií s ich súradnicami na mape7.
| Pozícia | ID pozície |
|---|---|
| \([0, 0]\) | \(1\) |
| \([1, 1]\) | \(2\) |
| \([2, 3]\) | \(3\) |
- V druhej boli pozície priradené číslam a názvom kolónií.
| ID pozície | ID kolónie | Kolónia |
|---|---|---|
| \(1\) | \(1\) | Jablkovo |
| \(2\) | \(2\) | Hruškovo |
| \(3\) | \(0\) | Malinovo |
- V tretej sa nachádzal zoznam dvojíc čísel kolónií, ktoré je potrebné prepojiť tunelom.
| ID kolónie \(a\) | ID kolónie \(b\) |
|---|---|
| \(1\) | \(2\) |
| \(0\) | \(2\) |
Po pár mesiacoch bol plán projektu hotový a išlo sa stavať, no nastal problém. Druhá tabuľka sa záhadne stratila, a tak sú v projekte len súradnice a prepojenia čísel kolónií. Nevieme ale, ktorá kolónia je na ktorých súradniciach.
Stavebníci teraz nevedia, kde treba stavať. Skúste ale z projektu zachrániť, čo sa dá: navrhnite také riešenie, ktoré teoreticky môže byť pôvodne zamýšľaný plán.
Úloha
Na Marse sa nachádza \(n\) kolónií. Poznáte ich \(n\) celočíselných súradníc \(x, y\), avšak, neviete konkrétne, ktorá pozícia prislúcha ktorej kolónii. Pozície sú navzájom rôzne, a žiadne tri pozície neležia na jednej priamke.
Ďalej máte plán projektu, v ktorom sú zapísané dvojice čísel \(a, b\) označujúce kolónie, medzi ktorými má viesť obojsmerný tunel. Táto vlaková sieť tvorí graf-strom: je teda súvislá a vedie v nej práve \(n-1\) hrán.
Navrhnite, medzi ktorými pozíciami majú viesť tunely tak, aby sa žiadne dva tunely nekrižovali, a aby jednotlivé pozície v nejakom poradí zodpovedali jednotlivým kolóniám.
Vstup
V prvom riadku vstupu sa nachádza číslo \(1 \leq n \leq 1\,000\) udávajúce počet kolónií. Nasleduje \(n - 1\) riadkov. V každom z nich sa nachádzajú dve čísla \(a, b\) hovoriace, že medzi kolóniami \(a\) a \(b\) má byť postavený tunel. Kolónie číslujeme \(0, 1, \ldots, n-1\).
Ďalej nasleduje \(n\) riadkov. V \(i\)-tom z nich sa nachádzajú dve čísla \(x_i, y_i\), súradnice \(i\)-tej pozície nejakej kolónie. Tieto súradnice v absolútnej hodnote nepresiahnu \(10^9\).
Výstup
Na výstup vypíšte \(n - 1\) riadkov. V každom z nich nech je dvojica čísel \(a, b\), ktorá znamená, že medzi \(a\)-tou pozíciou a \(b\)-tou pozíciou má viesť tunel. Pozície číslujeme od \(0\) po \(n-1\).
Na poradí tunelov ani na poradí čísel \(a\) a \(b\) vo výstupe nezáleží. Ak je správnych odpovedí viac, vypíšte ľubovoľnú z nich.
Je zaručené, že každý vstup má platné riešenie.
Príklady
Input:
3
1 2
0 2
0 0
1 1
2 3Output:
0 1
1 2Máme tri kolónie. Očíslované sú \(0\), \(1\) a \(2\). Tunel má viesť medzi kolóniami \(1\) a \(2\) a medzi kolóniami 0 a 2. Tri pozície sú \([0, 0]\), \([1, 1]\) a \([2, 3]\). Príkladový výstup hovorí, že spojíme pozíciu číslo \(0\) s pozíciou \(1\) a tiež \(1\) s \(2\). To znamená, že jeden tunel bude medzi \([0, 0]\) a \([1, 1]\) a druhý medzi \([1, 1]\) a \([2, 3]\). Keby sme si to znázornili na štvorčekovú sieť súradníc, videli by sme, že sa žiadne dva tunely nepretínajú. Okrem toho je zachovaný aj spôsob prepojenia kolónií: Buď by bola kolónia číslo \(1\) v \([0, 0]\) a kolónia \(0\) v \([2, 3]\), alebo naopak.
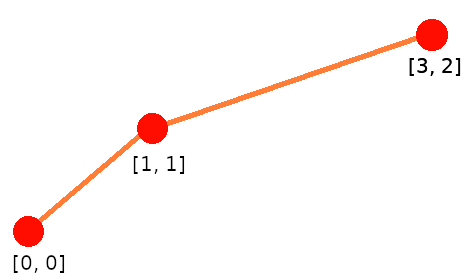
Iné platné riešenie by mohlo spojiť pozície \(1\) s \(2\) a \(2\) s \(0\)
Input:
5
0 1
1 2
2 3
3 4
0 0
9 9
2 3
3 2
7 8Output:
0 3
3 1
1 4
4 2Podľa tohto výstupu by boli tunely postavené takto:
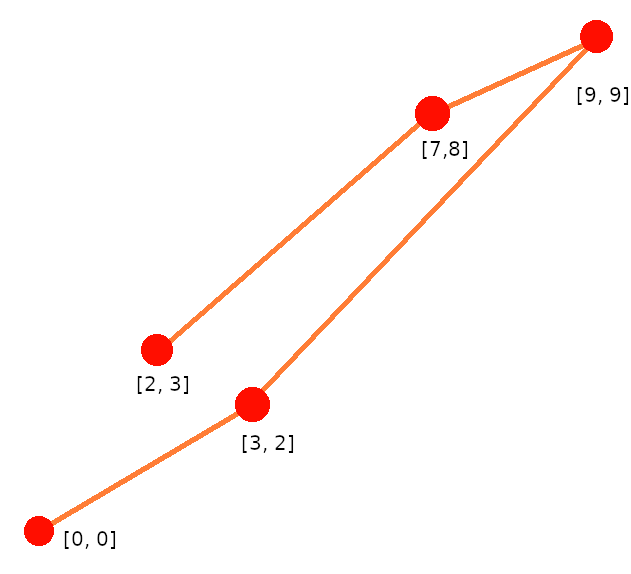
Posledné informácie hovoria o počte \(197\,359\)↩
Narodili sa už na Marse↩
Pricestovali na Mars↩
Keďže budú chránené v podzemí↩
1373 km/h↩
Ani predseda Medzinárodnej rady vesmírnych agentúr nevedel zdôvodniť toto rozhodnutie↩
Aj keď je jasné, že Mars nie je plochý, pre účely tejto úlohy postačí, že povrch Marsu budeme považovať za rovinu a použijeme obyčajnú karteziánsku súradnícovú sústavu.↩
Odovzdávanie
Na odovzdávanie sa musíš prihlásiť
Otázky a diskusia
Po skončení kola budete mať príležitosť na diskutovanie o riešeniach v diskusii pod vzorovým riešením.