4. Éra pečúceho slnka

Za posledný týždeň sa Emo spálil na slnku každý deň. Jeho frajerku to už prestalo baviť, takže teraz sa musí každé ráno natrieť opaľovacím krémom.

Emo sa okolo ôsmej, keď ešte slnko tak nepáli, vydá zo svojho domčeku do jediného domčeku v meste, ktorý má opaľovací krém. Do tohto domčeku nemusí viesť priama cesta, preto po ceste bude musieť navštíviť niekoľko ďalších domčekov, ktoré sú poprepájané chodníkmi. Medzi každými dvoma domčekmi je najviac jeden chodník ktorý ich spája. Aby nemusel zbytočne šliapať, zvolí si trasu najkratšiu – teda takú, ktorá vedie cez čo najmenej domčekov.

Vy z výšin sledujete Emov osud a nechcete, aby jeho život skĺzol do každodennej rutiny a chodil každý deň tou istou cestou. Radi by ste sieť chodníkov navrhli tak, aby tam najkratších možných ciest bolo viacero.

Rozhoďte kocky osudu na stôl, máchnite žezlom večnosti a vymyslite plán mesta, ktorý bude mať vyššími mocnosťami stanovený počet rôznych najkratších trás!

Úloha

Od vyšších mocností dostanete číslo \(k\). Vašou úlohou bude vytvoriť taký plán mesta – domčekov a chodníkov medzi nimi – v ktorom vedie medzi dvoma zvolenými domčekmi práve \(k\) rôznych najkratších ciest. A aby mesto nebolo príliš veľké, môže mať najviac tisíc domčekov.

Formát vstupu

Vstup obsahuje jedno jediné číslo \(k\) (\(1 \leq k \leq 1\,000\,000\,000\)) – počet najkratších možných ciest medzi Emovým domčekom a opaľovacím krémom.

Formát výstupu

Správny výstup tvorí popis ľubovoľného mesta spĺňajúceho všetky zadané podmienky.

Popis mesta musí mať nasledovnú formu. Na prvom riadku výstupu sú dve medzerou oddelené čísla – \(d\) a \(c\). Číslo \(d\) označuje počet domčekov vo vašom meste a musí preň platiť \(2 \leq d \leq 1\,000\). Číslo \(c\) označuje počet chodníkov v meste a musí preň platiť \(1 \leq c \leq 1\,000\,000\). Nasledujúcich \(c\) riadkov výstupu popisuje jednotlivé chodníky.

Domčeky v meste si očíslujeme od 1 po \(d\). Domček číslo 1 je dom, v ktorom býva Emo a domček číslo \(d\) dom, v ktorom je opaľovací krém. Popis chodníka je tvorený dvoma medzerou oddelenými číslami – číslami domčekov, ktoré tento chodník spája. Po chodníkoch sa dá chodiť v oboch smeroch, a preto môžu byť uvedené v ľubovoľnom poradí. Teda chodník \(2~1\) je ten istý ako chodník \(1~2\).

Vo vami uvedenom meste by malo platiť, že medzi domčekmi 1 a \(d\) vedie práve \(k\) rôznych najkratších ciest.

Hodnotenie

Vaše riešenia budú testované na ôsmych sadách testovacích vstupov, pre ktoré platí:

Príklad

Input:

1

Output:

2 1
1 2

Výsledné mesto má dva domčeky a jeden chodník vedúci medzi nimi. Ale správny by bol napríklad aj popis mesta s troma domčekmi a dvoma cestami, ktoré by viedli medzi domčekmi \(1~2\) a \(2~3\).

Input:

3

Output:

10 11
8 5
3 6
2 9
5 9
7 4
3 1
8 3
2 4
1 7
10 9
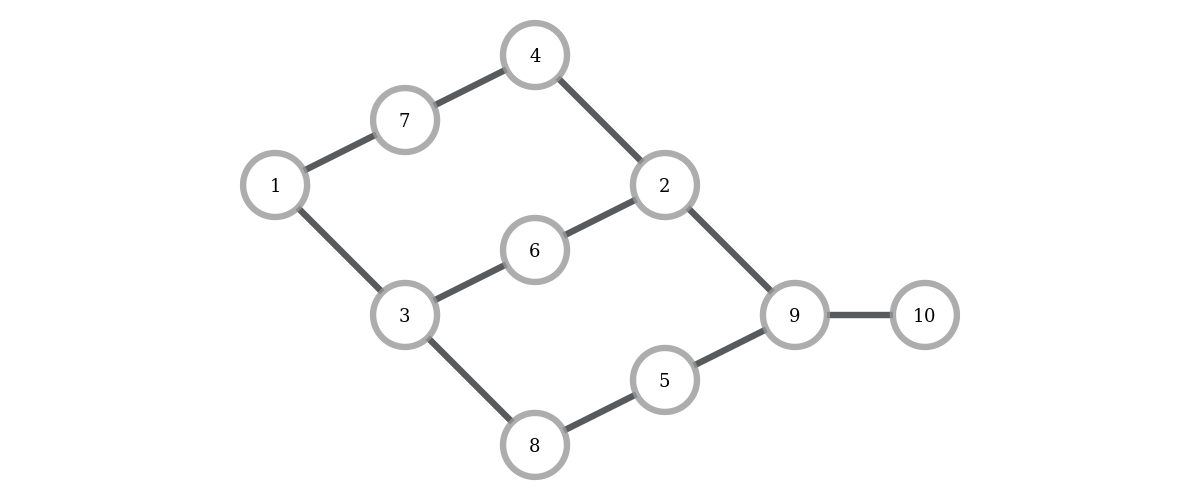
6 2

V tomto príklade sú tri rôzne najkratšie cesty dĺžky 5. Sú to cesty \(1-7-4-2-9-10\), \(1-3-6-2-9-10\) a \(1-3-8-5-9-10\).