Zadanie
Julka má veľa psíkov. A ono je to veľmi super vec, až do momentu, keď s toľkými psíkmi musí ísť von. Tak si vymyslela takýto plán: Keďže býva v dome s veľkou záhradou, tak len skontroluje, či je poriadne zatvorená brána a vždy keď nejaký psík chce ísť von, tak ho pustí, nech si behá po dvore. Chvíľu to fungovalo fajn, ale potom zistila, že musí stále sledovať, či nejaký psík nechce ísť von alebo dnu. Dvierka pre psíky ešte nemá namontované. Po pár dňoch si však všimla, že každý psík ide von len jeden krát za deň a to vždy v rovnakom čase a na rovnako dlho. Julka si zapísala tento interval pre každého psíka a teraz by si chcela nakresliť rozvrh časov. Na to ale potrebuje vedieť, aké široké stĺpčeky môže kresliť. Bohužial má Julka veľmi veľa úloh a fakt veľa psíkov, tak nemá čas si to sama spočítať. Pomôžete jej?
Úloha
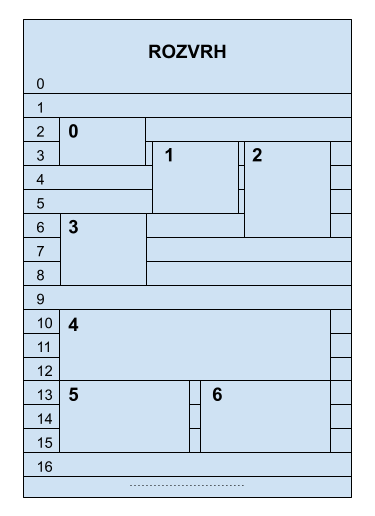
Rozvrh má jeden stĺpec pre celý deň, ktorý je rozdelený po milisekundách. V tomto rozvrhu budeme značiť intervaly jednotlivých psíkov. Ak sa však dva intervaly prekrývajú, musíme každý zaznačiť len na polovicu stĺpca, ak sú 3 tak na tretinu a tak ďalej (viď obrázok). Julka dáva veľký dôraz na konzistenciu, takže ak sa dva intervaly niekde prekrývajú, musia byť ich časti v rozvrhu rovnako široké. Stĺpček pre jeden interval navyše musí byť v každom úseku rovnako široký (nemôže niekde byť širší, lebo je tam viac intervalov a niekde užší, lebo je tam menej intervalov). Vašou úlohou je pre každý interval vypísať, akú časť stĺpčeka zaberie v rozvrhu.
Formát vstupu
Na prvom riadku vstupu sa nachádza celé číslo \(n\) – počet psíkov. Nasleduje \(n\) riadkov, kde každý z riadkov obsahuje dve celé čísla \(s_i\) a \(e_i\), pričom \(s_i\) je čas vypustenia \(i\)-teho psíka do záhrady a \(e_i\) je čas návratu \(i\)-teho psíka do domu, \(0 \leq s_i < e_i < 10^9\), psík je vonku počas intervalu \(\langle s_i, e_i )\).
Formát výstupu
Vypíšte \(n\) riadkov, na každom z nich jedno celé číslo \(a_i\) – \(i\)-ty psík zaberie v rozvrhu \(1/a_i\) stĺpčeka.
Hodnotenie
Sú 4 sady vstupov, v ktorých platia tieto obmedzenia:
| Sada | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(1 \leq n \leq\) | \(100\) | \(1\,000\) | \(10\,000\) | \(100\,000\) |
Príklad
Input:
3
1 3
2 5
6 7Output:
2
2
1Input:
3
1 3
2 5
4 6Output:
2
2
2Keďže psíci 1 a 3 nie sú v záhrade naraz, vie ich Julka vyznačiť do rovnakého stĺpca.
Na začiatok si môžeme všimnúť, že na poradí, v akom sú intervaly na vstupe nezáleží. Prvá vec čo by nás mala v takomto prípade napadnúť, je zoradiť vstup.
Pomalé riešenie
Pozrime sa najprv, ako vôbec zistiť správnu odpoveď. Zo zadania si môžeme všimnúť, že v rozvrhu budú akési skupinky intervalov, ktoré sa niekde prekrývajú a teda majú všetky rovnakú šírku. Keď si intervaly zoradíme podla času začiatku, asi nás neprekvapí, že takéto skupinky budú tvoriť súvislé úseky. Stačí si uvedomiť, že ak takáto skupinka niekde končí, tak všetky ďalšie intervaly musia začínať až za koncom každého intervalu z tejto skupinky.
Ostáva nám už len tieto skupinky identifikovať a zistiť, akú majú šírku. Skupinku môžeme vytvárať tak, že budeme postupne pridávať intervaly z našeho utriedeného poľa, a aby sme zistili či doň patrí ďaľší interval, budeme si pamätať najväčšie číslo z koncov intervalov v danej skupinke.
Zistiť šírku je o niečo ťažšie, no zatiaľ sa uspokojíme s tým, že po každom pridanom intervale sa pozrieme koľko z doterajších sa s ním prekrýva – teda končí neskôr ako začína on. Na prvý pohľad sa to možno nezdá, ale takýto prístup naozaj bude fungovať. Určite nám takto nevyjde väčší výsledok ako by mal, lebo všetky intervaly, na ktoré sa pozeráme sa prekrývajú s našim začiatkom, teda sa musia prekrývať aj navzájom. Už nám stačí sa len zamyslieť, pri ktorom intervale nájdeme to hľadané maximum prekrývajúcich sa intervalov. Spomedzi tých intervalov ktoré sa v tom momente prekrívajú, niektorý začína ako posledný. Keďže začína ako posledný, všetky ostatné máme už pridané a teda ich nájdeme ako prekrývajúce sa a vyjde nám správna maximálna šírka.
Rôzne vylepšenia
Môžeme si všimnúť, že jediná problematická časť v predošlom riešení je tá, kde zisťujeme šírku. Ak máme skupinku, ktorá obsahuje veľa intervalov (napríklad všetky), dosiahli by sme až kvadratickú časovú zložitosť. Potrebujeme teda zistiť, ako to robiť šikovnejšie.
Jedna možnosť je pozrieť sa na to ako na čiastkový problém a použiť vhodnú dátovú štruktúru. Napríklad binárne vyhladávacie stromy alebo haldu. Takéto riešenie môže byť napríklad v C++ pomerne jednoduché, no Python nemá takúto štruktúru v štandardnej knižnici. Pozrime sa teda radšej na iné a krajšie riešenie.
#include <iostream>
#include <set>
#include <vector>
#include <algorithm>
using namespace std;
int main(){
int n;
cin>>n;
vector<pair<pair<int,int>,int>> ints(n);
for(int i=0; i<n; i++){
cin>>ints[i].first.first>>ints[i].first.second;
ints[i].second=i;
}
sort(ints.begin(),ints.end());
multiset<int> active;
vector<int> outs(n,0);
vector<int>s;
int p=0;
int k=0;
for (int i=0; i<n; i++){
active.insert(ints[i].first.second);
if (ints[i].first.first<k){
s.push_back(ints[i].second);
auto it = active.begin();
while (it != active.end() and *it <=ints[i].first.first) it = active.erase(it);
p = max(p, (int)active.size());
k = max(k,ints[i].first.second);
}
else{
for(int t=0; t<s.size(); t++) outs[s[t]]=p;
s={ints[i].second};
k=ints[i].first.second;
p=1;
}
}
for(int t=0; t<s.size(); t++) outs[s[t]]=p;
for(int i=0; i<n; i++) cout<<outs[i]<<endl;
}Užitočný trik
Ukážeme si trik ktorý nám pomôže ku jednoduchšiemu riešeniu. Tento prístup sa niekedy nazýva aj zametanie a spočíva v tom, že sa budeme posúvať od začiatku časovej osy po koniec a počítať si kolko intervalov je v danom momente aktívnych. Aby sme však neprechádzali všetky čísla, v ktorých sa nič nedeje, najprv si do jedného poľa uložíme všetky začiatky a konce intervalov, spolu s informáciou o tom, či ide o začiatok alebo koneic a ktorému intervalu patrí. Následne toto pole usporiadame podľa času (začiatku resp. konca), a prechádzame cyklom od začiatku po koniec. Pamätáme si počet aktívnych intervalov, pričom ak nejaký skončí, zmenšíme počet o jeden a ak nejaký začne, tak zase zväčšíme o jeden.
Ku kompletnému riešeniu nám stačí si pamätať najväčší počet aktívnych intervalov a zoznam intervalov, ktoré sme už stretli. Keď narazíme na situáciu, že máme nula aktívnych intervalov, znamená to, že nejaká skupinka skončila. Zapíšeme si aktuálne maximum pre všetky uložené intervaly, vynulujeme maximum a uložené intervaly, a pokračujeme.
Časová a pamäťová zložitosť
Takéto riešenie má časovú zložitosť \(O(n\cdot \log(n))\) kvôli usporiadaniu poľa. Pamäťová zložitosť bude lineárna, pretože každé číslo zo vstupu budeme mať uložené len konštantný počet krát, a nič naviac.
n = int(input())
ints = [list(map(int,input().split()))+[i] for i in range(n)]
changes=[]
for i in ints:
changes.append((i[0],1,i[2]))
changes.append((i[1],-1,i[2]))
changes.sort()
outs =[0 for _ in range(n)]
ctr=0
m=0
s=[]
for n,c,i in changes:
ctr+=c
m=max(m,ctr)
if c==1:
s.append(i)
if ctr==0:
for t in s:
outs[t]=m
s=[]
m=0
print(*outs, sep='\n')Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.