8. Inovatívny dážď vzorové riešenie

9
1 1     // Pozicie laviciek
1 5
3 4
4 1
4 2
5 1
1 6
2 6
1 7
1 2     // Cesticky
1 3
1 4
2 7
4 5
4 6
7 8
7 9
5
1 9 1
1 1 2 7
1 9 1
1 1 1 7
8 3 2
1 3 4 6
1 1 2 2
5 8 3
1 1 4 2
1 3 2 6
5 5 8 9
3 5 1
3 1 4 4

NIE
OK
OK
OK
NIE

Možno ste si všimli, že táto úloha je nápadne podobná sedmičke z minulého kola. To veru nie je náhoda, vznikla pri písaní checkeru na tú sedmičku :) Tak sa pusťme do toho, veď napísať checker nemôže byť ťažšie ako originálne riešenie, či?¹

Riešenie za tri body

Získať tri body nie je tak ťažké – každý obdĺžnik overíme v lineárnom čase: najskôr si nájdeme cestu v strome medzi vrcholmi, ktoré nás zaujímajú (na to postačí napríklad obyčajné DFSko), a potom pre každý vrchol skontrolujeme, či leží, alebo neleží v nejakom obdĺžniku. Ak vrchol leží na ceste, ale neleží v žiadnom obdĺžniku, vypíšeme NIE, a rovnako vypíšeme NIE, ak niektorý vrchol neležiaci na ceste zas leží v nejakom obdĺžniku.

Takéto riešenie má čas \(O(n)\) na query, takže celková časová zložitosť je \(O(nq)\) a pamäťová \(O(n)\).

Koľko všetkých vrcholov leží v obdĺžniku?

Predstavme si najskôr zjednodušenú úlohu: daný je obdĺžnik, koľko vrcholov stromu v ňom leží? Keby sme mali miesto obldĺžnika iba 1D interval? Potom je úloha ľahko riešiteľná intervaláčom! A keď sa nad tým zamyslíme, tie obdĺžniky nie sú od intervalov až tak odlišné, takže tiež použijeme intervaláč, avšak 2D intervaláč!

2D intervalový strom

2D intervalový strom je intervalový strom, ktorý má v každom vrchole intervalový strom. Zdá sa to kus abstraktné?

Pozrime sa na obrázok:

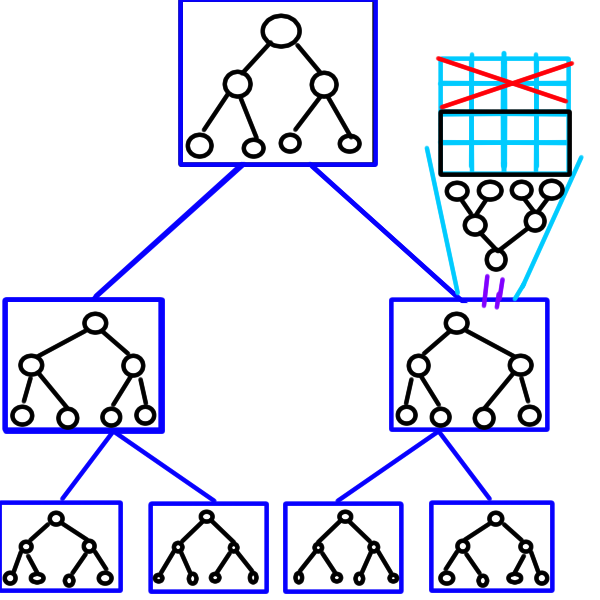
Majme vrchol vo “veľkom” intervaláči, pokrývajúci interval \([a, b)\). Povedzme, že tieto intervaláče pokrývajú x-ovú súradnicu. V tomto vrchole je druhý intervaláč rovnakej veľkosti. Ten si v intervale \([c, d)\) pamätá hodnotu z políčok \([a, b)\times[c, d)\).

My chceme súčtový intervaláč, z ktorého dostaneme počet vrcholov v obdĺžniku, takže si tento “malý” intervaláč pamätá počet vrcholov v obdĺžniku s rohmi \((a, c)\) a \((b, d)\).

Update jedného políčka v intervaláči nám zaberie \(O(\log^2 n)\) času, keďže najskôr potrebujeme updatnúť \(O(\log n)\) “malých” intervaláčov po ceste. Podobne, query zaberie \(O(\log^2 n)\) času.

Zdá sa však, že tento veľký 2D intervaláč zaberie veľa miesta: má \(2n\) vrcholov, a ak je v každom jeden intervaláč zaberajúci \(O(n)\) pamäte, potrebujeme až \(O(n^2)\) pamäte! Už to začína znieť nerealizovateľne, avšak povšimnime si kontrast medzi pamäťovou a časovou zložitosťou: ak potrebujeme updatnúť \(n\) vrcholov, použijeme \(O(n\log^2 n)\) času, ale až \(O(n^2)\) pamäte! Teda veľa inicializovanej pamäte je vstutku zbytočnej. Čo s tým?

Môžeme použiť múdru, lenivú implementáciu intervaláča: každý vrchol (aj v “malom” intervaláči) má pointre (smerníky) na svoje dve deti (alebo NULL ak deti ešte neboli upravované). Ak príde query do vrchola a chcela by ísť do niektorého neexistujúceho dieťaťa, vrátime za daného potomka odpoveď nula. Ak príde update, ktorý by potreboval updatovať aj nejakého neexistujúceho potomka, potomka vytvoríme a pustíme update rekurzívne ďalej.

Takže vieme zaručiť, že nedostaneme asymptoticky horšiu pamäťovú zložitosť ako časovú zložitosť na update queries, teda \(O(n\log^2 n)\).

Už sa blížime k riešeniu otázky: koľko všetkých vrcholov leží v obdĺžniku?

Najskôr si predpripravíme takýto 2D intervalový strom a updatneme \(+1\) na políčka, kde ležia vrcholy.

Následne, pre každý obdĺžnik, povedzme s rohmi v \((x_1, y_1)\) a \((x_2, y_2)\), zavoláme query: ako v bežnom intervaláčovom hľadaní ideme po “veľkom” intervaláči, kým nie je rozsah x-súradníc vrcholu (povedzme že \([a, b)\)) podmnožina intervalu x-súradníc nášho obdĺžnika (teda \([x_1, x_2)\)). V takomto vrchole pokračujeme naše hľadanie do “menšieho” intervaláča, kde následne nájdeme počet vrcholov so súradnicami \(a \leq x < b\) a \(y_1 < y_2\).

Takto vieme rovnako ako v normálnom 1D intervaláči vyskladať celý obdĺžnik, a teda získame počet vrcholov ležiacich v obdĺžniku.

Avšak, nejako stále ignorujeme otázku, ako zistiť, či vrcholy na nejakej ceste ležia v obdĺžniku?

Leží cesta v obdĺžniku?

Ďalší krok v ceste za riešením je zistenie, koľko vrcholov z nejakej cesty leží v obdĺžniku.

Nápad je nasledovný: Použijeme perzistentný intervaláč, a to konkrétne tak, že keď sa pozrieme na intervaláč v konkrétnom čase, bude to súčtový intervaláč vrcholov na nejakej ceste od koreňa do vrchola. Poďme sa na to pozrieť bližšie:

Perzistentný 2D intervaláč

Cieľom je mať intervalový strom, v ktorom sa vieme pýtať query nielen do priestoru, ale aj v čase – teda otázky typu: aký je súčet na tomto obdĺžniku pred \(u\) updatmi?

Ako sa to dá robiť? Používame 2D intervaláč naprogramovaný pomocou pointerov. Vždy, keď sa vrchol má updatnuť, neuložíme zmenu priamo – miesto toho vytvoríme nový, updatnutý vrchol.

Pre lepšiu ilustráciu použime obrázok:

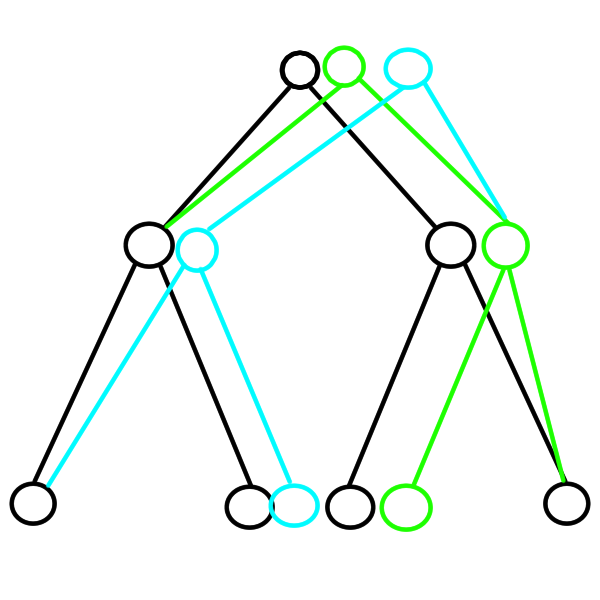
Pri updatnutí tretieho listu (pozície 3) vytvoríme nový list (zelenou). Následne updatujeme jeho rodiča (keďže sa vytvorilo nové, updatnuté dieťa). Na staré dieťa nazabúdame, starý rodičovský vrchol ostáva ako je, ale vytvárame nový zelený vrchol, ktorému ako deti dáme aktuálne verzie synov (teda ľavý zelený list a pravý čierny list). Následne ideme zas hore, a vytvoríme nový koreň, ktorého pointer do pravého syna ukazuje práve na náš nový zelený vrchol.

Keďže my máme intervaláče v intervaláčoch, musíme ešte domyslieť technické detaily, čo ako, keď robíme tieto updaty. Napríklad “malé” intervaláče máme uložené vo vrcholoch väčšieho intervaláča ako pointre, a pri každom update dostaneme nový pointer, na nový koreň “malého” intervaláča, ktorý potom uložíme v novom vrchole.

A nie je toto nejaké pomalé? Veď predsa vytvárame veľa nových vecí!

Ale keď sa nad tým zamyslíme, nie je ich v skutočnosti až tak veľa. Pre každý update updatneme \(O(\log n)\) vrcholov vo veľkom intervaláči a pre každý tento vrchol updatneme ešte \(O(\log n)\) vrcholov v malom intervaláči. Takže dokopy dostaneme zložitosť \(O(log^2n)\) času aj pamäte na jednu update query, čo je pomerne akceptovateľné.

Použitie perzistentného intervaláča

Ako tento perzistentný intervaláč použiť?

Začneme s prázdnym 2D perzistentným intervaláčom. Zakoreňme si strom a prehľadávajme ho DFSkom. Kedykoľvek prídeme do nového vrcholu, pridajme \(+1\) na jeho súradnicu v intervaláči. Kedykoľvek z vrcholu nadobro odídeme, pridajme \(-1\) na jeho súradnicu v intervaláči.

Takto, keď sme v akomkoľvek vrchole, aktuálny stav intervaláča (ten po poslednom update) je, že sú \(+1\) na všetkých predkoch vrchola (do tých sa už DFS dostalo, ale ešte ich neopustilo nadobro), ale zároveň, ak sme nejaký vrchol už navštívili, ale nie je predok, museli sme ho aj opustiť, takže na jeho súradnici je \(+1-1 = 0\). Ak sme nejaký vrchol ešte nenavštívili, intervaláč si preň pamätá \(0\) (resp. si nepamätá nič, keďže sme sa k updatovaniu súradnice ešte nedostali, ale pre to, ako intervaláč funguje, to je rovnaké, ako keby tam bola nula).

Takže keď chceme dostať stav, že jediné \(+1\) sú na súradniciach vrcholov na ceste z koreňa do nejakého vrchola \(v\), stačí si zobrať koreň intervaláča z updatu hneď po navštívení \(v\).

Už sa blížime ku koncu, ostávajú technické detaily.

A čo pre akúkoľvek cestu?

Akúkoľvek cestu v strome vieme rozdeliť na dve slížovité cesty od najbližšieho spoločného predka dole (pozri napríklad kuchárku).

Najbližšieho spoločného predka vieme nájsť napríklad v čase \(O(1)\) s predpočítaním \(O(n\log n)\).

Keď máme takto rozdelené cesty, pre každú cestu získame počet vrcholov v obdĺžniku zvlásť, a keďže LCA leží na oboch, odrátame \(1\), ak leží v obdĺžniku.

Ako to teda nájsť pre peknú slížovitú cestu z predka \(p\) do potomka \(v\)? Vieme nájsť koľko vrcholov je v obdĺžniku pre cestu z koreňa do \(v\). Chceli by sme odrátať tie vrcholy, ktoré ležia na ceste medzi koreňom a \(p\). Ale to vieme, zistíme koľko je vrcholov v obdĺžniku na ceste medzi koreňom a rodičom \(p\) (aby sme neodrátali \(p\)), a to odčítame od počtu vrcholov v obdĺžniku na ceste medzi koreňom a \(v\). A hurá, dostali sme, čo sme chceli.

A ako teda odpovedať na queries?

Poďme si to zrekapitulovať.

Dostaneme query vo forme dvoch vrcholov, \(a\) a \(b\), a zopár (\(k\)) obdĺžnikov. Obdĺžniky sa zaručene neprekrývajú, takže máme o jeden kameň na srdci menej.

Zistime najskôr, koľko je všetkých vrcholov v strome ležiacich v obdĺžnikoch (to vieme, obyčajným 2D intervaláčom) v \(O(k\log^2 n)\) čase.

Zistime, koľko vrcholov na ceste medzi \(a\) a \(b\) leží v obdĺžnikoch. Tiež to vieme zistiť v čase \(O(k\log^2 n)\).

Pochopiteľne, tieto dva údaje sa musia rovnať, inak kričíme NIE (inak by nejaký vrchol mimo cesty ležal v obdĺžniku).

Ak sa rovnajú, to stále nie je automatické áno: môže sa stať, že v obdĺžnikoch leží menej vrcholov z cesty, ako má. Ako toto overiť? Jednoducho, stačí nám navyše zistiť počet vrcholov na ceste a porovnať ho s počtom vrcholov z cesty ležiacich v obdĺžnikoch.

Počet vrcholov na ceste sa dá zistiť jednoducho: zapamätáme si výšku každého vrchola, a potom dĺžka cesty je:

\[v_a + v_b - 2v_\text{lca}\]

Kde \(v_a\) je výška \(a\), \(v_b\) je výška \(b\) a \(v_\text{lca}\) je výška najbližšieho spoločného predka. Tak, a toto nám dáva online odpoveď na query v \(O(k\log^2 n)\) čase. Na predpočítanie sme použili čas \(O(n\log^2 n)\) (na vybudovanie intervaláča a predpočítanie LCA, a teda celková časová zložitosť je \(O((n + q k_\text{max}) \log^2 n)\) a pamäťová \(O(n\log^2 n)\).

#include <bits/stdc++.h>
using namespace std;

struct node_1d {
    int xstart, xrange;
    node_1d *prvy, *druhy;
    int sum;
    
    node_1d(int N) {
        xstart = 0;
        xrange = N;
        sum = 0;
        prvy = NULL, druhy = NULL;
    }
    
    node_1d(int start, int range, int update_to, int change) {
        xstart = start;
        xrange = range;
        sum = change;
        if (range != 1) {
            int child_range = range / 2;
            if (update_to < child_range + start) {
                prvy = new node_1d(start, child_range, update_to, change);
                druhy = NULL;
            }
            else {
                prvy = NULL;
                druhy = new node_1d(start + child_range, child_range, update_to, change);
            }
        }
        else {
            prvy = NULL;
            druhy = NULL;
        }
    }
    
    node_1d(node_1d *previous, int update_to, int change) {
        if (previous -> xrange == 1) {
            xstart = previous -> xstart, xrange = previous -> xrange;
            prvy = NULL, druhy = NULL;
            sum = previous -> sum + change;
        }
        else {
            int child_range = previous -> xrange / 2;
            xrange = previous -> xrange, xstart = previous -> xstart;
            sum = previous -> sum + change;
            if (update_to < xstart + child_range) {
                if (previous -> prvy == NULL) prvy = new node_1d(xstart, child_range, update_to, change);
                else prvy = new node_1d(previous -> prvy, update_to, change);
                druhy = previous -> druhy;
            }
            else {
                if (previous -> druhy == NULL) druhy = new node_1d(xstart + child_range, child_range, update_to, change);
                else druhy = new node_1d(previous -> druhy, update_to, change);
                prvy = previous -> prvy;
            }
        }
    }
    
    int query(int z, int k) {
        if (xstart >= k || xstart + xrange <= z) return 0;
        if (z <= xstart && k >= xstart + xrange) return sum;
        return (prvy == NULL ? 0 : prvy->query(z, k)) + (druhy == NULL ? 0 : druhy -> query(z, k));
    }
};

struct node_2d {
    int ystart, yrange;
    node_1d *seg_tree;
    node_2d *prvy, *druhy;
    
    node_2d(int N) {
        ystart = 0;
        yrange = N;
        seg_tree = new node_1d(N);
        prvy = NULL, druhy = NULL;
    }
    
    node_2d(int start, int range, int to_x, int to_y, int change, int N) {
        ystart = start, yrange = range;
        seg_tree = new node_1d(0, N, to_x, change);
        if (range == 1) {
            prvy = NULL, druhy = NULL;
        }
        else {
            int child_range = range / 2;
            if (start + child_range > to_y) {
                druhy = NULL;
                prvy = new node_2d(start, child_range, to_x, to_y, change, N);
            }
            else {
                prvy = NULL;
                druhy = new node_2d(start + child_range, child_range, to_x, to_y, change, N);
            }
        }
    }
    
    node_2d(node_2d *prev, int to_x, int to_y, int change, int N) {
        yrange = prev -> yrange, ystart = prev -> ystart;
        seg_tree = new node_1d(prev -> seg_tree, to_x, change);
        if (yrange != 1) {
            int child_range = yrange / 2;
            if (ystart + child_range > to_y) {
                if (prev -> prvy == NULL) prvy = new node_2d(ystart, child_range, to_x, to_y, change, N);
                else prvy = new node_2d(prev -> prvy, to_x, to_y, change, N);
                druhy = prev -> druhy;
            }
            else {
                prvy = prev -> prvy;
                if (prev -> druhy == NULL) druhy = new node_2d(ystart + child_range, child_range, to_x, to_y, change, N);
                else druhy = new node_2d(prev -> druhy, to_x, to_y, change, N);
            }
        }
        else {
            prvy = NULL, druhy = NULL;
        }
    }
    
    int get_sum(int x1, int x2, int y1, int y2) {
        if (y1 >= ystart + yrange || y2 <= ystart) return 0;
        if (y1 <= ystart && y2 >= ystart + yrange) {
            int res = seg_tree -> query(x1, x2);
            return res;
        }
        return (prvy != NULL ? prvy -> get_sum(x1, x2, y1, y2) : 0) + (druhy != NULL ? druhy -> get_sum(x1, x2, y1, y2) : 0);
    }
    
};

struct persistent_2dsegment_tree {
    int N;
    vector<node_2d *> roots;
    
    persistent_2dsegment_tree(int n) {
        N = pow(2, ceil(log2(n)));
        roots.push_back(new node_2d(N));
    }
    
    int update(int x, int y, int change) {
        int kam = roots.size();
        roots.push_back(new node_2d(roots.back(), x, y, change, N));
        return kam;
    }
    
    int query_sum(int time_start, int time_end, int x1, int y1, int x2, int y2) {
        int end = roots[time_end] -> get_sum(x1, x2, y1, y2);
        int start = roots[time_start] -> get_sum(x1, x2, y1, y2);
        return end - start;
    }
};

void dfs_to_segtree(int v, int f, persistent_2dsegment_tree *segtree, vector<int> &Z, vector<vector<int> > &hrany, vector<int> &X, vector<int> &Y) {
    int id = segtree -> update(X[v], Y[v], 1);
    Z[v] = id - 1;
    for (int w : hrany[v]) {
        if (w == f) continue;
        dfs_to_segtree(w, v, segtree, Z, hrany, X, Y);
    }
    segtree -> update(X[v], Y[v], -1);
}

void dfs_euler(int v, int f, int h, vector<vector<int> > &hrany, vector<pair<int, int> > &euler, vector<int> &ID, vector<int> &H) {
    ID[v] = (euler.size());
    H[v] = h;
    euler.push_back({h, v});
    for (int w : hrany[v]) {
        if (w == f) continue;
        dfs_euler(w, v, h + 1, hrany, euler, ID, H);
        euler.push_back({h, v});
    }
}

struct rmq {
    int N;
    vector<vector<pair<int, int> > > R;
    
    rmq() {}
    
    rmq(int n, vector<pair<int, int> > &A) {
        N = n;
        int id = 0;
        int jump = 1;
        R.push_back(A);
        
        while (jump < n) {
            R.push_back(vector<pair<int, int> >(n));
            for (int i = 0; i < n; i ++) {
                R[id + 1][i] = min(R[id][i], (i + jump < n ? R[id][i + jump] : make_pair(N, N)));
            }
            id ++;
            jump *= 2;
        }
    }
    
    int query(int a, int b) {
        if (a > b) swap(a, b);
        int id = log2(b - a);
        return min(R[id][a], R[id][b - (1 << id)]).second;
    }
};

struct checker {
    int n;
    vector<vector<int> > hrany;
    vector<int> X, Y, Z, H, ID;
    persistent_2dsegment_tree *segtree;
    persistent_2dsegment_tree *all;
    int ind;
    rmq R;
    
    checker(int n, vector<vector<int> > &hrany, vector<int> &xcoor, vector<int> &ycoor): n(n), hrany(hrany), X(xcoor), Y(ycoor), segtree(new persistent_2dsegment_tree(n)), all(new persistent_2dsegment_tree(n)) {
        Z.resize(n);
        ID.resize(n);
        H.resize(n);
        vector<pair<int, int> > euler;
        dfs_to_segtree(0, -1, segtree, Z, hrany, X, Y);
        dfs_euler(0, -1, 0, hrany, euler, ID, H);
        R = rmq(2 * n - 1, euler);
        
        for (int i = 0; i < n; i ++) {
            ind = all -> update(X[i], Y[i], 1);
        }
        
    }
    
    bool check(int a, int b, int k, vector<int> x1, vector<int> y1, vector<int> x2, vector<int> y2) {
        for (int i = 0; i < k; i ++) {
            x1[i] --;
            y1[i] --;
        }
        
        int ida = ID[a], idb = ID[b];
        int lca = (a == b ? a : R.query(ida, idb));
        
        int count_in = 1 + (H[a] - H[lca]) + (H[b] - H[lca]);
        int count = 0;
        
        for (int i = 0; i < k; i ++) {
            int in_all = all -> query_sum(0, ind, x1[i], y1[i], x2[i], y2[i]);
            int path_in = segtree -> query_sum(Z[lca], Z[a] + 1, x1[i], y1[i], x2[i], y2[i]);
            
            path_in += segtree -> query_sum(Z[lca], Z[b] + 1, x1[i], y1[i], x2[i], y2[i]);
            
            
            if (x1[i] <= X[lca] && x2[i] > X[lca] && y1[i] <= Y[lca] && y2[i] > Y[lca]) {
                path_in --;
            }
            if (in_all != path_in) return false;
            count += path_in;
        }
        return (count == count_in);
    }
    
};

int main() {
    int n;
    cin >> n;
    vector<vector<int> > hrany(n);
    vector<int> X, Y;
    
    for (int i = 0; i < n; i ++) {
        int x, y;
        cin >> x >> y;
        X.push_back(x - 1);
        Y.push_back(y - 1);
    }
    
    for (int i = 0; i < n - 1; i ++) {
        int a, b;
        cin >> a >> b;
        a --, b --;
        hrany[a].push_back(b);
        hrany[b].push_back(a);
    }
    checker C(n, hrany, X, Y);
    
    int q;
    cin >> q;
    
    for (int i = 0; i < q; i ++) {
        int a, b;
        cin >> a >> b;
        a --, b --;
        int k;
        cin >> k;
        vector<int> x1(k), x2(k), y1(k), y2(k);
        for (int j = 0; j < k; j ++) {
            cin >> x1[j] >> y1[j] >> x2[j] >> y2[j];
        }
        cout << (C.check(a, b, k, x1, y1, x2, y2) ? "OK" : "NIE") << endl;
    }
}