Zadanie
Obchod Kde Sú Potraviny sa rohodol zaviesť bezpečnostné opatrenia proti rozsiahlemu postihnutiu políc prázdnotou. V KSP totiž zistili, že ľudia majú tendenciu prísť do obchodu s istým cieľom, a kúpiť si to čo chcú. Toto však vôbec nie je dobré. Keď príde veľa ludí s rovnakým cieľom, ostávajú prázdne police.
Zaviedli preto nový systém nakupovania. Zákazníkovi pridelia jednu policu ku ktorej sa postaví, podľa minuty od otvorenia v ktorej prišiel. Zákazník sa môže potom rozhodnúť, či to čo je na danej polici kúpi a odíde, alebo to nechce, hodí si mincou a posunie sa podľa nej doprava alebo doľava1. Tý KSPáci sú ale kreatívny, že?
Marcela poslala jeho žena Sabinka do KSP nakupovať. Keďže vie o týchto opatreniach, nedala mu klasický nákupný zoznam, ale ku každej položke čo v obchode majú mu napísala, ako veľmi ju chce. Marcel sa pred cestou zamyslel, a uvedomil si, že ak vôjde v správnom čase, má väčšiu šancu kúpiť niečo, čo Sabinka chce viac. Ale kedy je ten správny čas?
Úloha
Na vstupe dostanete Sabinkino ohodnotenie všetkých vecí v obchode, zoradené tak, ako sú na policiach (na každej jedna vec). Vašou úlohou je zistiť, v ktorej minúte má Marcel prísť (teda na ktorej polici má začať svoj nákup), aby očakávaná hodnota toho čo kúpi bola čo najvyššia. Očakávaná hodnota sa dá vyrátať ako váhovaný priemer hodnoty podľa pravdepodobnosti, že Marcel kúpi jednotlivé veci. Môžete predpokladať, že v každom prípade by Marcel nechal svoj osud na náhodu, len ak by to zvíšilo jeho očakávaný zisk oproti tovau pri ktorom práve stojí. Aby sa Marcel vedel rozhodnúť aj keď niektorú minutu zmešká, vypíšte mu očakávaný zisk pre každú policu.
Formát vstupu
Na prvom riadku sa nachádza číslo \(n\), (\(1\leq n \leq 100\,000)\) počet políc v obchode. Na druhom riadku je \(n\) čísel, (\(0\leq x_i \leq 10^9\)), Sabinkino ohodnotenie jednotlivích políc s tovarom.
Formát výstupu
Vypíšte \(n\) riadkov, na \(i\)-tom z nich očakávanú hodnotu Marcelovho nákupu ak začne pri \(i\)-tej polici. Čísla vypisujte s presnosťou aspoň na 5 desatinných miest.
Príklad
Input:
2
1 3Output:
1.5
3Ak začne pri prvej polici, neoplatí sa mu zobrať daný tovar, lebo ak si hodí mincou má polovičnú šancu že vypadne a získa tak \(0\) ale polovičnú šancu skončiť na druhej polici a zobrať \(3\). To je v priemere \(1.5\), čo je viac ako \(1\).
Input:
6
2 3 6 13 4 1Output:
3.25
6.5
9.75
13
8.66666
4.33333Ak je pri prvej alebo poslednej polici, môže sa stať že vypadne z obchodu, a nekúpi nič.↩︎
Prvým krokom ku vzorovému riešeniu, je nájsť aspoň nejaké riešenie. Prvá myšlienka čo by nás mohla napadnúť je, že ak by sme poznali riešenie pre pozície \(i-1\) a \(i+1\), tak vieme zistiť riešenie pre index \(i\) ako \(r[i]=max(h[i],\dfrac{r[i-1]+r[i+1]}{2})\), kde \(h[i]\) je hodnota na vstupe. Berieme teda tú lepšiu z Marcelovich možností. Buď zoberie to kde je alebo si hodí mincou a jeho očakávaný zisk bude priemer toho, čo by teoreticky získal vpravo a toho, čo vľavo. Rýchlo však prídeme na to, že túto rovnicu len tak ľahko nevyriešime, lebo má celkom nepríjemné vlastnosti. Skúsený algebraik by v tom možno uvidel inverzné matice a začal by písať riešenie v \(O(n^3)\), ale to my našťastie nie sme.
Môžeme si však všimnúť, že vo výsledku musí na všetkých políčkach platiť spomenutá rovnica a vo vstupnom poli je určite niekde porušená (inak by bolo rovno aj riešením). Skúsme teda tieto chybi vo vstupnom poli postupne opravovať a dúfať, že skončíme na tom správnom riešení. A hľa, na sampli to funguje a aj testovač nám dá nejaké body.
Zamyslíme sa však, prečo to vlastne funguje a to nás privedie ku vzoráku. Skúsme si to nakresliť. Nasledujúce dva obrázky ukazujú, čo sa deje, keď postupne aplikujeme túto rovnicu (postupne priemerujeme hodnoty \(r[i-1]\) a \(r[i+1]\), čo nám posúva čiaru hore). Na osi x je index v poli a na osi y je hodnota v poli. Najspodnejšia čiara ukazuje vstupné čísla a najvrchnejšia výstup. Prvý je vyobrazený 00.sample.b.in, druhý je 01.a.in.
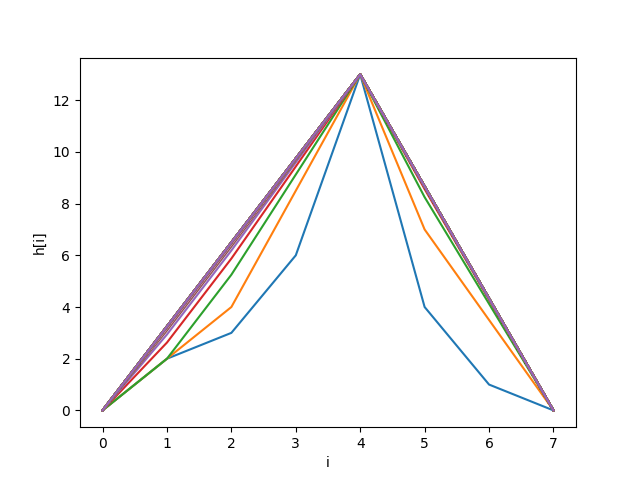
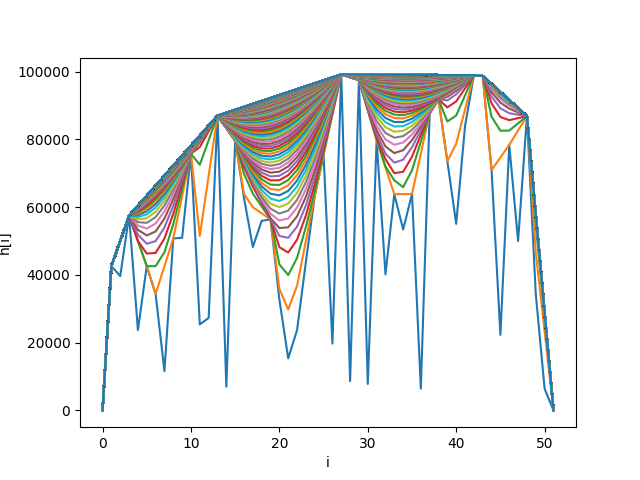
Na týchto obrázkoch celkom jasne vidíme, že to čo hľadáme je vlastne horný konvexný obal.
Prečo je to tak?
Prečo práve konvexný obal? Ľahko vidíme, že na konvexnom obale je naša rovnica naozaj všade splnená. priemer totiž vždy padne na alebo pod konvexný obal. Na druhej strane vidíme body, na ktorých sa konvexný obal láme. Na týchto miestach priemer nikdy nebude vyšší ako pôvodná hodnota. Marcel preto na tomto mieste mincou hádzať nebude. Na miestach medzi dvomi takýmito bodmi si Marcel bude hádzať mincou, až kým sa dostane na jeden z nich. Očakávanú hodnotu teda naozaj predstavuje úsečka, ktorá ich spája (čím bližšie k jednému, tým väčšia pravdepodobnosť, že na ňom skončí skôr).
Časová a pamäťová zložitosť
Naše riešenie spočíva naozaj len vo výpočte konvexného obalu čísel na vstupe, ktorý vieme spraviť v \(O(nlog(n))\). Ak si však yvolíme vhodný algoritmus pre konvexný obal, logaritmus môžeme vyhodiť, lebo čísla na vstupe máme zadané pekne zľava do prava a nepotrebujeme ich zoradiť a ostane nám iba \(O(n)\). Okrem toho, nám stačí na základe tohoto obalu vypísať správne hodnoty na výstup, čo už zvládneme v \(O(n)\). Pamäťová zložitosť je rovnako \(O(n)\) (vstup potrebujeme, a viac pamäte by sme aj tak nestihli využiť).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.