Zadanie
Voľby v Krajine Samých Politikov sú už za rohom.
Treba byť akční! Však ak s tým nič neurobíme, tí politici z opozície - Fakt Kool Strana - nebodaj získajú demokratickú väčšinu, postavia vládu, a začnú plniť svoje predvolebné sľuby! Koalícia Mnohých Strán tomu musí nejako zabrániť.
KMS sa teda rozhodla zorganizovať predvolebnú kampaň, na ktorej vycestujú z hlavného mesta a navštívia všetky okresné mestá, po čom sa slávnostne vrátia do hlavného mesta v deň volieb.
Mohli síce vyrátať najkratšiu cestu ktorú by museli prejsť, bol by to však problém. Ak by totiž navštívili okresné mestá v tak špecifickom poradí, žurnalisti z časopisu Zuby a Vlasy by si to určite vysvetlili tak, že na okresoch ktoré KMS navštívi posledné im nezáleží, a stratili by v nich voličov.
Keďže KMS nemá hlavného vedúceho ktorý by vedel takéto obvinenia verejne poprieť, rozhodlo sa KMS pre inú stratégiu - spravia okruhovú cestu krajinou. Začnú v hlavnom meste, ktoré je najzápadnejšie okresové mesto. Potom sa vydajú na východ, pričom ponavštivujú niektoré mestá, až kým neprídu do najvýchodnejšieho z nich. Vtedy spravia otočku a vydajú sa na západ, pričom navštívia všetky mestá ktoré vynechali v opačnom smere, až kým nakoniec neprídu naspäť do hlavného mesta.
Pomôžte KMSákom zrátať, koľko najmenej kilometrov musia prejsť, aby mohli takto zorganizovať svoju predvolebnú kampaň a poraziť FKS!
Úloha
Každé mesto si vieme predstaviť ako bod v rovine.
KMS začína v najzápadnejšom meste, a potom sa vydá na východ k najvýchodnejšiemu mestu. Po ceste môže navštíviť niektoré mestá, tie však musia mať rastúcu zemepisnú dĺžku (\(x\)-ovú súradnicu).
Po príchode do najvýchodnejšieho mesta sa KMS otočí a vydá na západ, pričom v klesajúcom poradí zemepisnej dĺžky navštívi všetky mestá, ktoré KMSáci nenavštívili počas kampaňovania na východ.
Akú najmenšiu vzdialenosť musia prejsť?
Formát vstupu
V prvom riadku vstupu je číslo \(n\) – počet miest v KSP. Každý z nasledovných \(n\) riadkov obsahuje dve čísla \(x_i y_i\): súradnice jedného mesta. Tie sú kladné a nepresahujú milión. Body budú udávané v rastúcom poradí zemepisnej dĺžky (teda žiadne mestá nemajú rovnakú zemepisnú dĺžku, a prvé mesto na vstupe je hlavné mesto).
Formát výstupu
Vypíšte najmenšiu vzdialenosť ktorú KMSáci musia prejsť aby zvládli svoju okruhovú predvolebnú kampaň. Dĺžku ich cesty meriame Euklidovsky.
Vypíšte dostatočne veľa desatinných miest. Vaša odpoveď bude uznaná, ak sa bude od našej líšiť v absolutnéj alebo relatívnej hodnote najviac \(10^{-6}\).
Hodnotenie
Čím väčšia sada, tým väčšie \(n\), zhora ohraničené postupne:
Počtom prstov na mojich rukách a nohách
Počtom dní v letných prázdninách
Počtom dní v orbite Venuše
Rokom v ktorom Krištof Kolumbus objavil Ameriku
\(n\) nikdy nie je menšie ako počet trpaslíkov v rozprávke o Snehulienke mínus päť.
Príklady
Input:
5
1 3
2 1
3 4
4 4
5 2Output:
10.870481593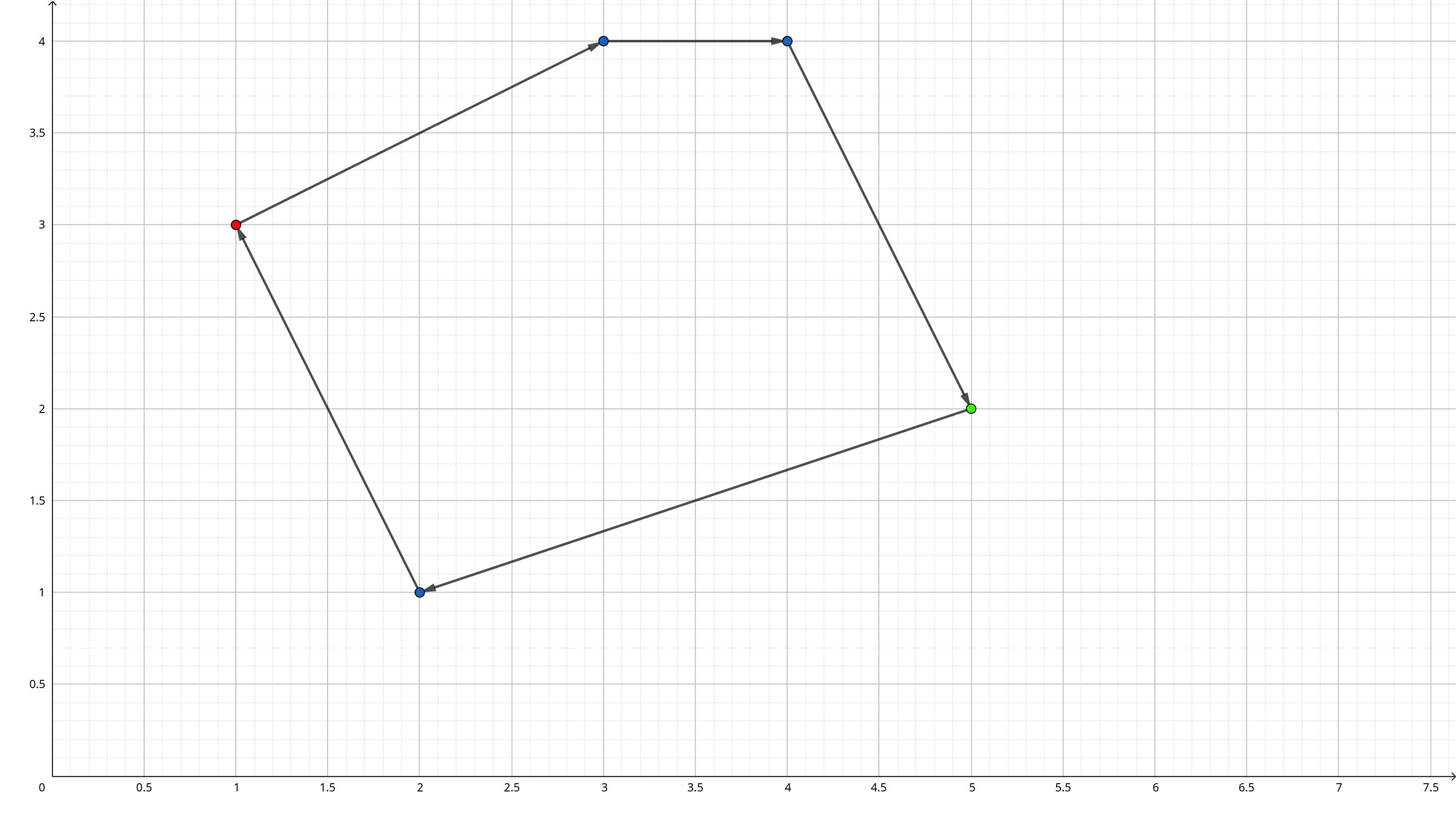
Input:
10
4 1
13 4
21 3
25 9
28 10
42 1
43 2
50 4
67 10
68 9Output:
131.651455225Hrubá sila
Ako vždy, na prvú sadu tejto úlohy nám postačí hrubá sila a málo rozmýšľania.
Chceme nájsť najkratšiu okruhovú cestu po mestách? No tak vyskúšajme všetky možné okruhové cesty, a zapamätajme si najlepší výsledok.
Každá okruhová cesta je jednoznačne určená tým, ktoré mestá navštívime cestou na východ (keďže všetky zvyšné mestá potom musíme jednoducho navštíviť počas cesty na západ). Toto si teda môžeme reprezentovať napríklad \(n-2\) bitmi v čísle; ak je \(i\)-ty bit čísla 1, navštívime ho cestou na východ, inak cestou na západ. Všetky možné cesty sú teda reprezentované číslami \(0\) až \(2^{n-2}-1\). Pre každé z nich si spravíme zoznam miest ktoré chceme navštíviť v jednom smere a ktoré v druhom, sčítame vzdialenosti medzi susednými mestami v oboch zoznamoch (nezabudnime zarátať hlavné a najvýchodnejšie mesto v oboch prípadoch), a zo všetkých takýchto súčtov si zapamätáme ten najmenší.
Časová zložitosť tohto riešenia je \(O(n2^n)\), keďže pre každú z \(O(2^n)\) okruhových ciest vyrátame jej dĺžku v \(O(n)\).
Pamäťová zložitosť nášho riešenie ja \(O(n)\), keďže si nepotrebujeme pamätať nič väčšie ako vstup.
Dynamické programovanie
Všetky rýchlejšie riešenia sú založené na rovnakom princípe – určíme si nejaké stavy, ktoré jednoznačne popisujú nejaký stav v ktorom sa nachádzame (ktoré mestá sme spracovali), a dynamickým programovaním so stavu ‘stojím v hlavnom meste a ešte som nič nenavštívil’ postupne nájdeme najmenšie vzdialenosti v stavoch s viac a viac spracovanými mestami, až nájdeme odpoveď pre všetky mestá. Riešenia sa potom len líšia tým, koľko stavov nakoniec budeme potrebovať, a ako rýchlo vieme vyskúšať všetky potrebné možnosti na zistenie vzdialeností susedných stavov. Tu si popíšeme rovno vzorové, ktoré zvláda všetky sady.
Okruhovú cestu si budeme predstavovať nie tak, že ideme najprv na východ a potom na západ, ale že máme dve skupiny ktoré idú zo západu na východ a medzi sebou navštívia všetky mestá. Ak naše skupiny navštívili všetky mestá od \(1\) až po \(k\), jediné čo potrebujeme vedieť na presunutie sa na ďalšie mesto je pre obe skupiny ich posledné navštívené mesto. Stačí nám na to teda tabuľka \(dp[n][n]\), pričom \(dp[i][k]\) obsahuje najmenšiu vzdialenosť čo dokopy naše dve skupiny prešli tak, aby najvýchodnejšie mesto navštívené prvou skupinou bolo \(i\), a druhou skupinou \(k\). Na začiatku teda nevieme žiadnu hodnotu okrem \(dp[1][1] = 0\), čo označuje obe skupiny vyrážajúce z hlavného mesta. Poznamenáme, že si nemusíme pamätať koľko miest sme už spracovali, keďže to už v stave implicitne je – spracovali sme \(max(i,k)\) miest.
Teraz pôjdeme po mestách zľava doprava. Povedzme že už vieme všetky optimálne prejdené vzdialenosti, aby naše dve skupinky navštívili všetky mestá od \(1\) po \(x\), a skúsme naše riešenia rozšíriť o mesto \(x+1\). Kľúčové pozorovanie je, že ak naše skupiny navštívili všetky mestá až po \(x\), pre jednu z nich je posledné navštívené mesto práve \(x\). Druhá skupina pritom môže byť v ľubovoľnom západnejšom meste (alebo v ňom práve v prípade \(x = 1\)). Vyskúšame teda všetky možnosti – ktorá z dvoch skupín je v meste \(x\), ktoré mesto naposledny navštívila druhá skupina, a ktorá z nich má navštíviť mesto \(x+1\). Dostaneme sa tak do nového stavu kde jedna zo skupín je v meste \(x+1\) a druhá ostala tam kde bola predtým. K vzdialenosti pripočítame cestu medzi dvoma mestami, ktoré zvolená skupina práve prešla a ak je menšia ako tá, ktorú sme doposiaľ objavili pre tento stav, zapamätáme si ju.
Postupne takto pozisťujeme najkratšiu potrebnú vzdialenosť ktorú skupiny musia prejsť tak, aby jedna z nich bola v meste \(n\), a druhá v nejakom predošlom meste \(m\), pre všetky \(1 \leq m < n\). Aby naša cesta bola ozaj okruhová, musíme k týmto vzdialenostiam ešte pripočítať vzdialenosť medzi mestom \(m\) a \(n\), aby sa obe skupiny nakoniec stretli v najvýchodnejšom meste. Zo všetkých týchto vzdialeností zoberieme najmenšiu, a to je naša odpoveď.
Časová a pamäťová zložitosť
Postupne zisťujeme najkratšie cesty pre každé ďalšie mesto, ktorých je \(n\). Pre každé z nich musíme skúsiť všetky predošlé mestá, ktoré mohla ako posledné navštíviť jedna zo skupín, a týchto možností je \(O(n)\). To že pre každé z nich skúšame ktorá zo skupín pricestuje do spracovávaného mesta, a ktorá zo skupín je tá vzdialená, je už len konštantne krát viac prípadov; časová zložitosť je teda \(O(n^2)\).
Pamätáme si pozície miest, čo nám zaberie \(O(n)\), a tabuľku \(dp\) o rozmeroch \(n\) krát \(n\), čiže naša pamäťová zložitosť je \(O(n^2)\). Ak by sme si udržiavali len posledné dva stĺpce našej dynamiky (poslednú a tú, ktorú práve rátame), môžeme to zlepšiť na \(O(n)\).
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.