4. Jeden smer vzorové riešenie

Zadanie

“Ideme dobrým smerom?” opýtal sa Maťko Kubka. Kubko mal kompas a Maťko mal mapu. “Ideme niekde medzi severom a východom.” povedal Kubko. Maťko sa pozrel na mapu a povedal: “Veľmi si mi nepomohol. Ak ideme skôr k severu, tak to minieme o desať kilometrov a ak viac k východu, tak možno aj o päť.” Kubko sa pozrel na kompas a zamyslel sa. Ak ideme viec k severu, to je vlastne medzi severom a severovýchodom. Ak je to bližšie k tomu severovýchodu, tak je to medzi severovýchodom a severoseverovýchodom a presne uprostred medzi nimi bol smer, ktorým išli. Kubko teda spokojne vyhlásil: “Ideme presne na severovýchodoseveroseverovýchod.”. Maťko sa usmial, a povedal: "Ďakujem, teraz viem, že ideme správne.

Viete aj vy akým smerom idú dvojičky Maťko a Kubko?

Úloha

Na vstupe dostanete názov nejakej svetovej strany a vašou úlohou je zistiť, akým smerom sa nachádza táto svetová strana. Aby sme vám to zjednodušili¹, chceme od vás uhol medzi severom a danou svetovou stranou, pri čom nechceme radiány, stupne, ani žiadne iné exotické zápisy, ale jednoducho číslo od \(0\) do \(1\). A toto číslo chceme v dvojkovej sústave.

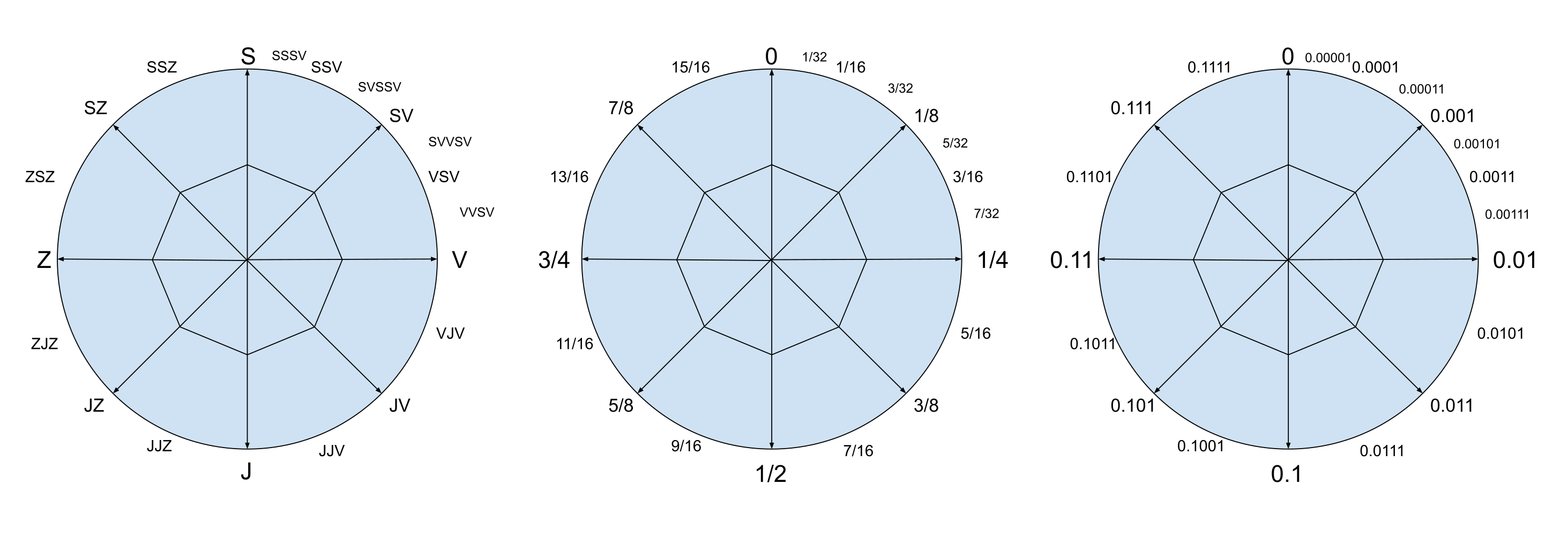
Názov svetovej strany vždy vznikne spojením dvoch svetových strán medzi ktorými sa nachádza. Nie však hocijakých (juho-severovýchod predsa neexistuje). Musia to byť strany “o úroveň vyššie”. Predstavme si že na prvej úrovni je sever, východ, juh, západ. Na druhej pridáme aj tie medzi nimi (teda S,SV,V,JV,J,JZ,Z,SZ). Môžete si všimnúť, že každá ďalšia nová strana už bude vznikať medzi dvoma stranami, z ktorých jedna vznikla na vyššej úrovni ako druhá. V takomto poradí ich aj skladáme. Máme teda severo-severovýchod a nie severovýchodo-sever, lebo sever vznikol už na prvej úrovni a severovýchod až na druhej.

Teraz sa pozrieme na uhly. Sever je \(0\), východ je \(1/4\), juh je \(1/2\) a západ \(3/4\). Uhol \(1\) by opäť predstavoval sever, ale to nebudeme používať, lebo sever je už \(0\). Ďalšie uhly sú jednoducho uprostred medzi susedmi. Juhozápad je teda medzi \(1/2\) a \(3/4\), a má uhol \(5/8\).

Na koniec sa pozrieme ako vyzerá binárny zápis. Nula je stále nula. V binárnej sústave predstavujú miesta naľavo smerom od desatinnej čiarky postupne hodnoty \(1\), \(2\), \(4\), \(8\), \(16\), … a tie na pravej strane, (desatinné² miesta) predstavujú zase postupne z ľava do prava \(1/2\), \(1/4\), \(1/8\), \(1/16\), … .

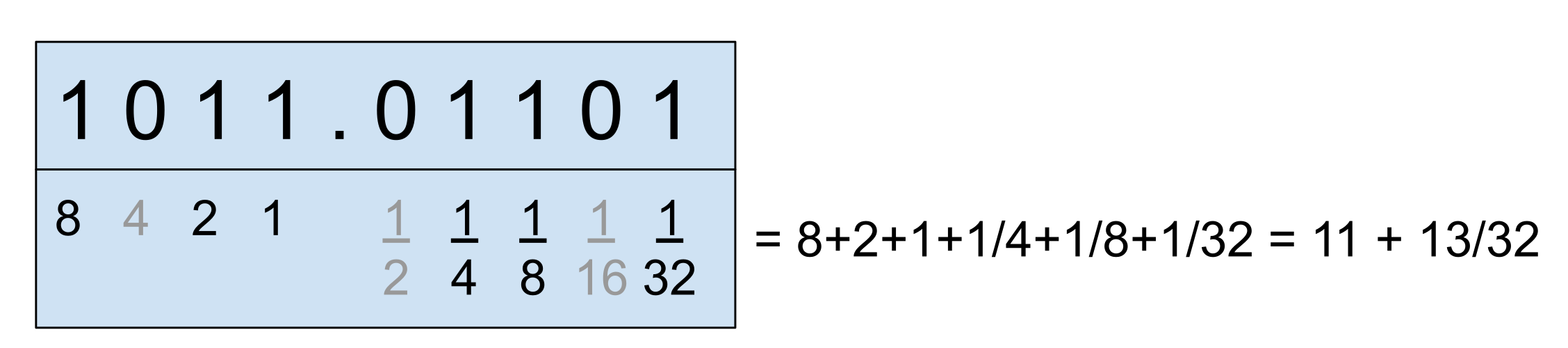
Napríklad \(13/16 = \boldsymbol{1}/2 + \boldsymbol{1}/4 + \boldsymbol{0}/8 + \boldsymbol{1}/16\), teda \(0.1101\) v dvojkovej sústave³.

Formát vstupu

Na vstupe je jeden riadok a na ňom skratka názvu svetovej strany. Skladá sa z veľkých písmen “S,V,Z,J”. Dĺžka tohoto slova nepresiahne \(10^7\)

Formát výstupu

Vypíšte jedno desatinné číslo v dvojkovej sústave, bez núl na konci s výnimkou nuly samotnej pre sever. Na oddelenie desatinných miest použite bodku, nie čiarku.

Príklady

Input:

SV

Output:

0.001

Sevorovýchod, \(1/8=0/2+0/4+1/8\)

Input:

SVVSV

Output:

0.00101

Sevorovýchodo-Východosevorovýchod, \(5/32=0/2+0/4+1/8+0/16+1/32\)

---

1. Áno, naozaj je to jednoduchšie.↩︎

2. v dvojkovej sústave skôr polovičné↩︎

3. pre odvážnejších: zapíšte v dvojkovej sústave \(1/3\)↩︎

Prečo binárny zápis a ako to funguje

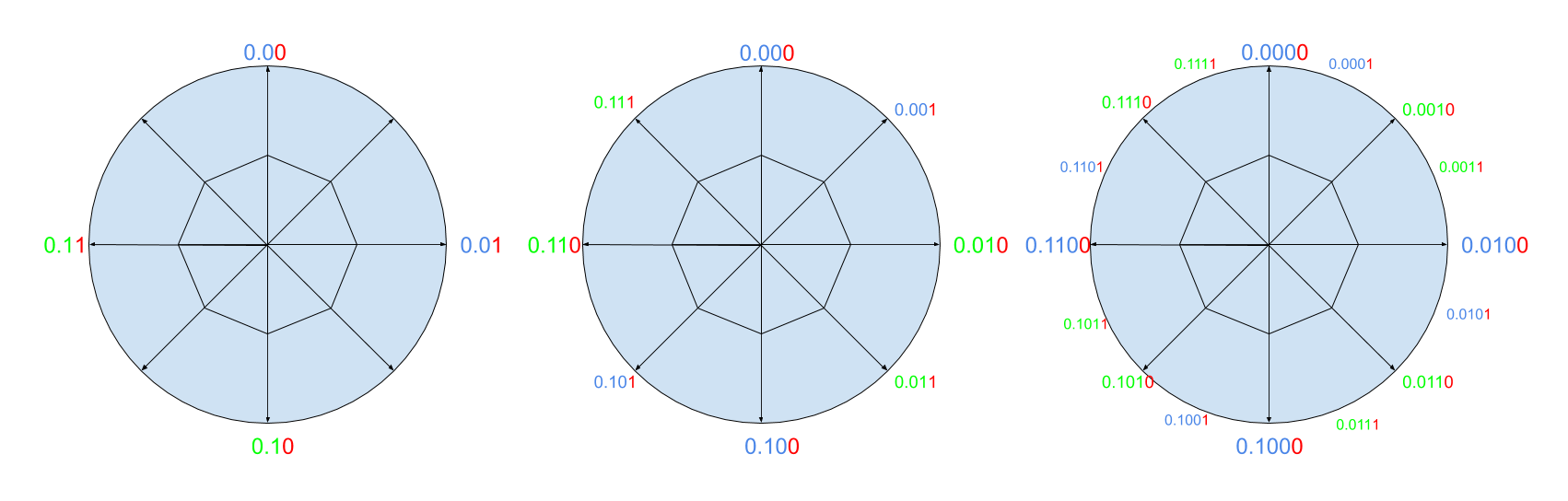
Binárny zápis riešenia sme zvolili pre to, že na to, aby sme zistili “uhol”, potom nepotrebujeme žiadne výpočty. Stačí nám zistiť, ako daný názov svetovej strany vznikol. Totiž keď zistíme v ktorej polovici je hľadaná strana, vieme jedno desatinné miesto. Keď zistíme štvrtinu, vieme dve. Keď osminu, vieme tri, a tak ďalej. Riešenie sa teda dá ľahko postupne spresňovať a ľahko sa dá vypísať aj ako dlhý reťazec bez nejakých problémov s presnosťou alebo upravovaním zlomkov. Nasleduje ešte jeden obrázok, na ktorom vidno ako toto “spresňovanie” funguje. Všimnite si, že zelené/modré časti vedla seba sú vždy rovnaké a na červených sa striedajú \(0\) a \(1\).

Naivné riešenie

Až \(4\) body získame za riešenie, ktoré bude postupne vytvárať všetky svetové strany, a s nimi aj uhly, ktoré ku nim prislúchajú. Následne nám stačí sa pozrieť do tohoto zoznamu a vypísať ten správny uhol, bez zbytočných núl na konci. Keď budeme tieto svetové strany vytvárať po úrovniach, ďalšiu úroveň vyrobíme tak, že vždy zoberieme uhol strany vľavo od nej a pripíšeme na koniec \(1\) (viď obrázok vyššie). Keď toto spravíme, treba ešte všetkým starým stranám pripísať na koniec \(0\), aby sa nám aj ďalej zachoval rovnaký počet desatinných miest. Zložitosť takéhoto riešenia je \(O(2^u)\) kde \(u\) je počet úrovní ktoré chceme vyrobiť. Aby náš odhad bol závislí len od veľkosti vstupu, môžeme ho zvýšiť na \(O(2^n)\) kde \(n\) je dĺžka vstupu, lebo vieme, že viac úrovní potrebovať určite nebudeme.

Vzorové riešenie

Prvá vec, čo si určite každý všimne je, že už z písmen ktoré máme na vstupe, vieme ľahko určiť štvrtinu, v ktorej je hľadaný smer. Ak sú to napríklad písmená S a V, vieme, že smer je niekde medzi severom a východom. Uhol ktorý hľadáme v binárnej sústave teda začína \(0.00\) (okrem prípadu kedy je to východ samotný a smer je už \(0.01\)).

Ďalší krok, ktorý by sme mali spraviť je, zistiť či sa nachádzame medzi S a SV alebo medzi SV a V. Keď to zistíme, budeme vedieť, že ďalšia cifra je \(0\) v prvom prípade resp. \(1\) v druhom prípade. Najprv však musíme pochopiť, ako toto skladanie strán prebieha. Keď si napíšeme názov nejakej strany, môžeme si ho “uzátvorkovať” tak, ako vznikal až po úroveň, kedy sú v samostatných zátvorkách jednotlivé písmená.

Aby to bolo prehľadnejšie, budeme to demonštrovať na obrázku, na strane VSVSVVSV. Každý rámček predstavuje jednu “zátvorku” a pod ním sú naznačené “zátvorky” v ňom, teda dve svetové strany, ktorých zložením vznikol. Farebné odlíšenie nám ešte ukazuje koľko zložení treba na vytvorenie danej srany. Názvy ktoré vznikli bez skladania - základné strany (čierna), strany ktoré vznikli jedným zložením (modrá), dve zloženia (červená), tri (modrá) a štyri (žltá).

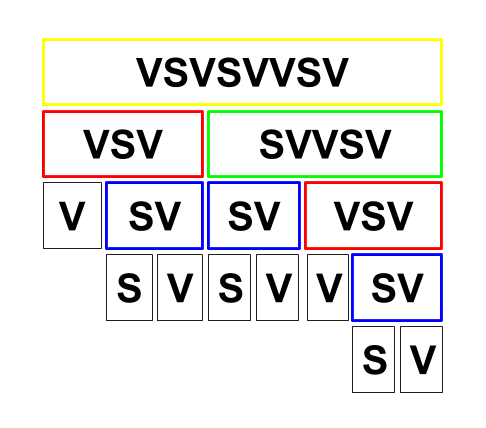
Na tomto obrázku si môžeme všimnúť napríklad to, že v jednej farbe sa vždy nachádza to isté (až na čiernu). Čo by sa stalo na ďalšej úrovni? To je veľmi jednoduché. Ďalšia úroveň vznikne tak, že pred tento názov prilepíme to, čo je vľavo alebo to, čo je vpravo od tejto strany. Teraz si stačí uvedomiť, že vlastne tento názov samotný vznikol ako spojenie toho vľavo, a toho vpravo, teda VSV a SVVSV. Keďže tieto dve veci už máme v našom obrázku (v druhom riadku), nič “nové” nám nepribudne.

Späť ku našej úlohe. Chceme zistiť, či sa nachádzame medzi S a SV aleo medzi V a SV. Pri ďalšom pohľade na obrázok zistíme, že S sa tam vždy nachádza iba ako priama súčasť SV, ale V sa tam nachádza aj ako súčasť iných strán (napr VSV). Keď sa nad tým ešte chvíľu zamyslíme, ľahko zistíme prečo je to tak. Ak sa nachádzame medzi SV a V a každá strana vzniká spojením okolitých dvoch, nemá sa tam ako dostať S samotné. Teda ak máme viac písmen V ako písmen S, vieme že okrem SV nám tam ostávajú práve písmená V. Máme teda ďalšiu cifru nášho dvojkového desatinného zápisu. Nakoľko sme išli do pravej polovice (pri pohľade zo stredu), je to \(1\) a teda máme \(0.001\).

Teraz nám ostáva celý proces opakovať. Vieme že sme medzi SV a V, a chceme zistiť, či vpravo alebo vľavo od VSV. Vieme teda, že celý názov je zložený zo SV a V a chceme zistiť, či je zložený z VSV a SV alebo VSV a V. Na to sa nám oplatí vedieť, koľko krát je tam SV a koľko V. Keď si na začiatku spočítame že \(\#_S=3\) a \(\#_V=5\) (mriežkou označujeme počet výskytov písmena) vidíme, že v ďalšom kroku \(\#_{SV}=\#_S\) a \(\#_V=\#_V-\#_S\). Teda minuli sme toľko V koľko je S aby sme ich pospájali do SV. Teraz opäť zistíme, čoho je viac a vieme ďalšiu cifru. Máme teda \(\#_{SV}=3\) a \(\#_V=2\), sme bližšie ku SV, teda medzi VSV a SV (uhol \(0.0010\)). Teraz položíme \(\#_{VSV}=\#_V=2\) a \(\#_{SV}=\#_{SV}-\#_V=1\). Sme teda bližšie ku VSV a máme uhol \(0.00101\). V ďalom kroku nám ostane \(\#_{SVVSV}=1\) a \(\#_{VSV}=1\), teda sme priamo medzi týmito dvoma stranami a finálny uhol je \(0.001011\) (posledná cifra nám vždy vyjde \(1\)).

Podobnosť tohto postupu s algoritmom na zistenie najväčšieho spoločného deliteľa sama o sebe naznačuje jednoduchosť implementácie.

Časová zložitosť takéhoto riešenia je \(O(n)\) od dĺžky slova na vstupe.

Iné riešenie

Z predošlého riešenia si môžeme všimnúť, že už počet písmen S a V, resp. Ich pomer, určuje jednoznačne uhol a je v jednom smere rastúci. Ak teda vieme desatinné dvojkové číslo previesť na názov strany (stačí aj počet písmen S a V), môžeme výsledný uhol binárne vyhľadávať.