4. Éra pečúceho slnka vzorové riešenie

Zadanie

Za posledný týždeň sa Emo spálil na slnku každý deň. Jeho frajerku to už prestalo baviť, takže teraz sa musí každé ráno natrieť opaľovacím krémom.

Emo sa okolo ôsmej, keď ešte slnko tak nepáli, vydá zo svojho domčeku do jediného domčeku v meste, ktorý má opaľovací krém. Do tohto domčeku nemusí viesť priama cesta, preto po ceste bude musieť navštíviť niekoľko ďalších domčekov, ktoré sú poprepájané chodníkmi. Medzi každými dvoma domčekmi je najviac jeden chodník ktorý ich spája. Aby nemusel zbytočne šliapať, zvolí si trasu najkratšiu – teda takú, ktorá vedie cez čo najmenej domčekov.

Vy z výšin sledujete Emov osud a nechcete, aby jeho život skĺzol do každodennej rutiny a chodil každý deň tou istou cestou. Radi by ste sieť chodníkov navrhli tak, aby tam najkratších možných ciest bolo viacero.

Rozhoďte kocky osudu na stôl, máchnite žezlom večnosti a vymyslite plán mesta, ktorý bude mať vyššími mocnosťami stanovený počet rôznych najkratších trás!

Úloha

Od vyšších mocností dostanete číslo \(k\). Vašou úlohou bude vytvoriť taký plán mesta – domčekov a chodníkov medzi nimi – v ktorom vedie medzi dvoma zvolenými domčekmi práve \(k\) rôznych najkratších ciest. A aby mesto nebolo príliš veľké, môže mať najviac tisíc domčekov.

Formát vstupu

Vstup obsahuje jedno jediné číslo \(k\) (\(1 \leq k \leq 1\,000\,000\,000\)) – počet najkratších možných ciest medzi Emovým domčekom a opaľovacím krémom.

Formát výstupu

Správny výstup tvorí popis ľubovoľného mesta spĺňajúceho všetky zadané podmienky.

Popis mesta musí mať nasledovnú formu. Na prvom riadku výstupu sú dve medzerou oddelené čísla – \(d\) a \(c\). Číslo \(d\) označuje počet domčekov vo vašom meste a musí preň platiť \(2 \leq d \leq 1\,000\). Číslo \(c\) označuje počet chodníkov v meste a musí preň platiť \(1 \leq c \leq 1\,000\,000\). Nasledujúcich \(c\) riadkov výstupu popisuje jednotlivé chodníky.

Domčeky v meste si očíslujeme od 1 po \(d\). Domček číslo 1 je dom, v ktorom býva Emo a domček číslo \(d\) dom, v ktorom je opaľovací krém. Popis chodníka je tvorený dvoma medzerou oddelenými číslami – číslami domčekov, ktoré tento chodník spája. Po chodníkoch sa dá chodiť v oboch smeroch, a preto môžu byť uvedené v ľubovoľnom poradí. Teda chodník \(2~1\) je ten istý ako chodník \(1~2\).

Vo vami uvedenom meste by malo platiť, že medzi domčekmi 1 a \(d\) vedie práve \(k\) rôznych najkratších ciest.

Hodnotenie

Vaše riešenia budú testované na ôsmych sadách testovacích vstupov, pre ktoré platí:

Sada	1	2	3	4	5	6	7	8
\[ 0 < k \leq \]	\(30\)	\(500\)	\(5000\)	\(10^{5}\)	\(10^{6}\)	\(10^{9}\)	\(10^{9}\)	\(10^{9}\)

Príklad

Input:

1

Output:

2 1
1 2

Výsledné mesto má dva domčeky a jeden chodník vedúci medzi nimi. Ale správny by bol napríklad aj popis mesta s troma domčekmi a dvoma cestami, ktoré by viedli medzi domčekmi \(1~2\) a \(2~3\).

Input:

3

Output:

10 11
8 5
3 6
2 9
5 9
7 4
3 1
8 3
2 4
1 7
10 9
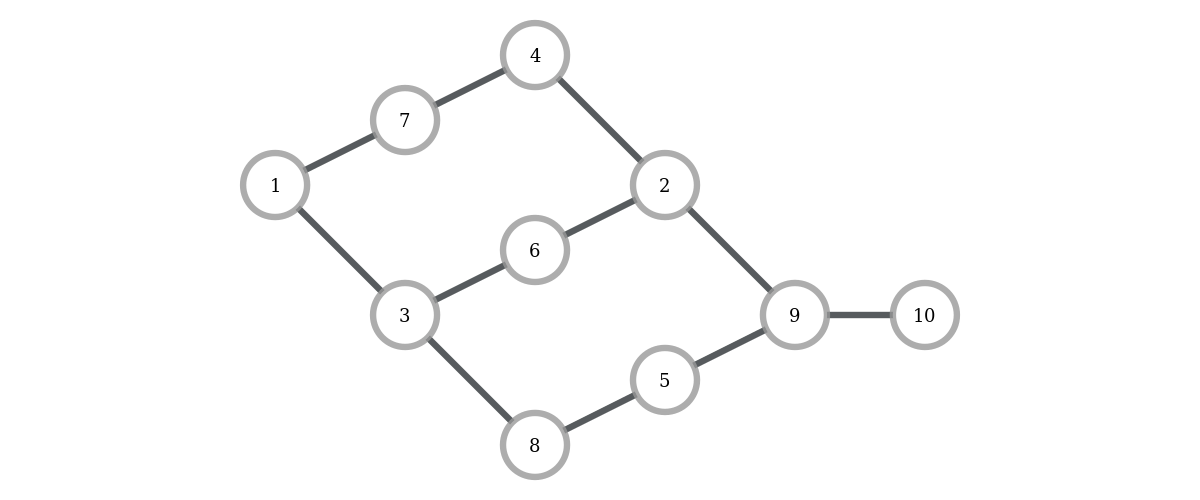
6 2

V tomto príklade sú tri rôzne najkratšie cesty dĺžky 5. Sú to cesty \(1-7-4-2-9-10\), \(1-3-6-2-9-10\) a \(1-3-8-5-9-10\).

Konštrukčná úloha, ktorá má neskutočné množstvo správnych riešení. Ukážeme si, čo je kameň úrazu tejto úlohy, čo s ním a nakoniec aj nejaké jedno možné¹ riešenie.

Kameň úrazu

Najtragickejšia veta zadania je tá, že počet domov vami navrhnutého mesta nesmie presiahnuť \(1\,000\). Prečo? Predstavme si, že by sme na toto nemali žiadne obmedzenie. Stačí nám vytvoriť niekoľko neprekrývajúcich sa ciest. Okrem štartovacieho a cieľového domu budeme mať v meste ešte \(k\) ďalších, prechodných domov. Každý prechodný dom spojíme chodníkom so štartom aj s cieľom.

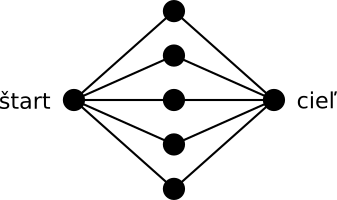
V našej úlohe je však počet ciest podstatne väčší, ako počet domov, ktoré môžeme použiť. Nejakým spôsobom potrebujeme na malý počet pridaných domov dosiahnuť veľký počet rovnako dlhých ciest. Dámy a páni, predstavujem vám:

Diamant

Diamantom budeme nazývať štyri domy spojené do kosoštvorca. Keď jeden z domov prehlásime za začiatok a dom oproti (cez uhlopriečku) za koniec, tak medzi nimi existujú práve 2 najkratšie cesty (dĺžky 2). Na tomto útvare je super, že sa dajú skladať za seba. Ak naskladáme 5 diamantov za seba (koniec jedného bude začiatkom druhého), dosiahli sme \(2^5=32\) možných rôznych najkratších ciest (každá postupnosť vľavo-vpravo-vľavo-vľavo-vľavo, vľavo-vpravo-vľavo-vľavo-vpravo, atď. je iná cesta). A to celé len za cenu \(3 \times 5 + 1 = 16\) domov.

Ak chceme \(2^{30} = 1\,073\,741\,824\) ciest, stačí naskladať 30 diamantov za seba, za cenu \(3 \times 30 + 1 = 91\) domov. Celkom dobré, nie?

Takže ak \(k\) je mocnina dvojky, len poskladáme príslušný počet diamantov. Čo však, ak nie je? Žiaden problém.

Príklad

Predstavme si, že \(k=10=8+2=2^3+2^1\). Toto nám vraví, že nejako by sa to mohlo dať, ak použijeme dve diamantové reťaze (série naskladaných diamantov), jednu zloženú z troch a druhú z jedného diamantu.

Reťaz s tromi diamantami obsahuje 8 ciest dĺžky 6, reťaz s jedným diamantom 2 cesty dĺžky 2. Keďže všetky cesty musia byť rovnako dlhé (aby boli všetky najkratšie), potrebujeme si cesty v kratšej reťazi nejako predĺžiť. To urobíme tak, že pred ňu pripojíme 4 vrcholy, ktoré nebudú mať inú úlohu, ako predlžovať cestu cez krátku reťaz. Takto upravené reťaze potom už len zapojíme vedľa seba (pridáme im spoločný štart a spoločný cieľ). Tadá.

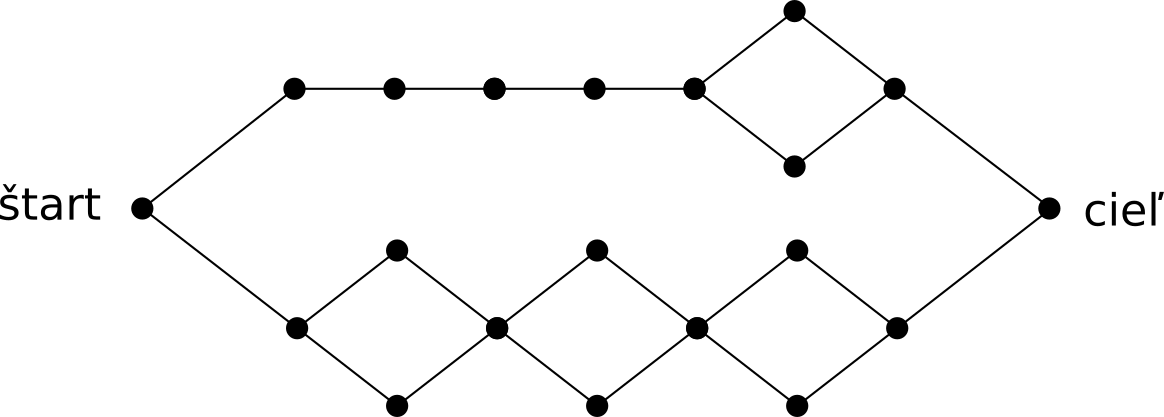
Takýmto postupom vieme vyskladať ľubovoľné číslo.

V kocke

Každé číslo sa dá zapísať v binárnom zápise. To predstavuje, z akých mocnín dvojky sa skladá. Napr. \(13 = 1101_2 = 2^3+2^2+2^0\). Pre tieto mocniny dvojky postavíme príslušné reťaze a všetky reťaze predĺžime na dĺžku najdlhšej. Takto upravené reťaze zapojíme vedľa seba a hotovo!

Koľko domov minieme?

Tak a teraz nepríjemná otázka s ešte horším zistením. Aby sme dokázali vytvoriť mesto s \(2^{29} - 1 = 536\,870\,911 = 11111111111111111111111111111_2\) najkratšími cestami (čo je stále menej ako maximálna hodnota zo zadania), potrebujeme všetky reťaze dĺžok \(1, 2, \dots, 28\). Už len vyskladanie tohto nám minie \(4 + 7 + 10 + \dots + 85 = 1246\) domov. Príliš veľa. Čo s tým vieme robiť?

Posledný trik

Trikom je nestavať veľa reťazí, ale iba jednu. Zo všetkých našich reťazí si necháme iba tú s najväčšou dĺžkou. Do tejto reťaze sa na niekoľkých miestach pripojíme vhodne dlhými cestičkami zo začiatku tak, aby sme využili len nejakú jej podčasť. Napríklad pre \(k = 50 = 110010_2\) to bude vyzerať takto:

Koľko stojí toto? Diamantová reťaz môže mať dĺžku najviac \(29\) diamantov, čo je \(29 \times 3+1 = 88\) domov. Okrem toho máme ešte začiatočný dom, koncový dom a cestičky pripájajúce sa na reťaz (takzvané slíže). Slíž pripájajúci sa na reťaz za \(x\)-tým diamantom má dĺžku \(2 x\). Ak by sme mali slíže všetkých možných dĺžok od 1 po 29 diamantov, dokopy by stáli \(2 + 4 + 6 + \dots + 58 = 870\) domov.

Dokopy teda nebudeme potrebovať viac než \(88 + 2 + 870 = 960\) domov a sme strašne šťastní, pretože to je pod \(1\,000\) :). Samozrejme, nejaké malé (a možno aj väčšie) optimalizácie sa ešte dajú porobiť, netreba ich však.

n = int(input())

MAX_POWER = 29  # 2^30 > 10**9
path_len = 1 + 2*MAX_POWER + 1

V = 2
E = []

# vytvorime chainu MAX_POWER diamantov na sebe, na vrchole 2
prev = V
V += 1
for _ in range(MAX_POWER):
    E.append([prev, V])
    E.append([prev, V+1])
    E.append([V, V+2])
    E.append([V+1, V+2])

    prev = V+2
    V = V+3

# vrchol pripojim na ciel
# este ale neviem presne, ake bude maximalne V, cize pouzijem nejaky sentinel
# preto taka velka hodnota
opalovak = 10**20
E.append([V-1, opalovak])

mocn, i = 1, 0
while mocn <= n:
    if mocn & n:
        # spravime sliz prislusnej dlzky
        # za kazdy missnuty diamant 2 vrchole
        prev = 1
        for _ in range(path_len - 2 - 2*i):
            E.append([prev, V])
            prev = V
            V += 1

        # a pripojime na spravne miesto do diamantu
        E.append([prev, 3*(MAX_POWER-i+1)-1])

    i += 1
    mocn *= 2

print(V, len(E))
for e in E:
    # iba opalovak bol vyssi nez V, takze iba unho bude hodnota teraz menena
    print(min(e[0], V), min(e[1], V))