2. Zajova paranoja vzorové riešenie

Zadanie

Zajo sa hral príliš veľa počítačových hier a teraz sa mu o nich aj sníva. Najhoršie sú nočné mory, v ktorých sa ho snaží odstreliť ostreľovač. Keď sa totiž Zajo z takejto nočnej mory prebudí, nevie sa zbaviť pocitu, že naňho cez okno niekto mieri a po celý zvyšok noci už nezaspí.

Preto si chce dať posteľ do takej časti izby, v ktorej ho nemajú šancu trafiť. Samozrejme, bol by rád, ak by táto bezpečná časť izby bola čo najväčšia (ani s pocitom, že niekto mieri na miesto desať centimetrov od vašej postele sa nespí veľmi dobre).

Úloha

Zajova izba má tvar obdĺžnika, ktorého strany sú rovnobežné so základnými svetovými stranami a má okná smerom na sever a na východ. Tieto okná sú veľmi úzke (človek, ktorý staval Zajovu izbu bol zrejme tiež paranoický) a pre účely tejto úlohy ich budeme považovať za body na stranách nášho obdĺžnika.

Ostreľovači, o ktorých sa Zajovi sníva, naňho mieria vždy buď z kopca ležiaceho presne na sever od Zajovho domu, alebo z vysokej budovy na východ od Zajovho domu. Takže ak ho chcú odstreliť, musia strieľať rovnobežne so stenami izby.

Poznáte rozmery miestnosti a pozície jednotlivých okien. Nájdite súvislú časť Zajovej izby neohrozenú ostreľovačmi, s najväčším obsahom.

Formát vstupu

Na prvom riadku vstupu sú 4 celé čísla \(x, y, m, n\), kde \(x\) a \(y\) sú rozmery izby (\(x\) je dĺžka severnej steny a \(y\) je dĺžka východnej steny), \(m\) je počet okien na severnej stene a \(n\) je počet okien na východnej stene. Platí \(1\leq x, y, m, n \leq 10^6\).

Na druhom riadku vstupu je \(m\) celých čísel \(x_1, \dots, x_m\): pozície jednotlivých okien na severnej stene. \(i\)-te okno je vo vzdialenosti \(x_i\) od severozápadného rohu Zajovej izby. Platí \(0 < x_1 < x_2 < \dots < x_m < x\) – okná sú teda zadané v poradí od západu na východ.

Na treťom riadku je \(n\) celých čísel \(y_1, \dots, y_n\): pozície jednotlivých okien na východnej stene. \(i\)-te okno je vo vzdialenosti \(y_i\) od juhovýchodného rohu izby. Platí \(0 < y_1 < y_2 < \dots < y_n < y\) – okná sú zadané v poradí od juhu na sever.

V 1. sade testovacích vstupov platí, že \(m,n \leq 10\), v 2. sade \(m,n\leq 1\,000\)).

Formát výstupu

Vypíšte jeden riadok a v ňom hodnotu \(S\), kde \(S\) je plocha (obsah) najväčšieho súvislého územia, na ktoré nemôže mieriť ostreľovač.

Môžete predpokladať, že \(S\) sa zmestí do bežnej 64-bitovej premennej. V C++ použite long long, v Pascale Int64.

Príklady

Input:

4 10 2 3
1 3
5 8 9

Output:

10

Input:

5 5 1 1
1
1

Output:

16

Input:

6 5 2 1
2 4
4

Output:

8

Situácie v jednotlivých príkladoch vyzerajú nasledovne (v poslednom príklade sú až tri rôzne časti s obsahom 8):

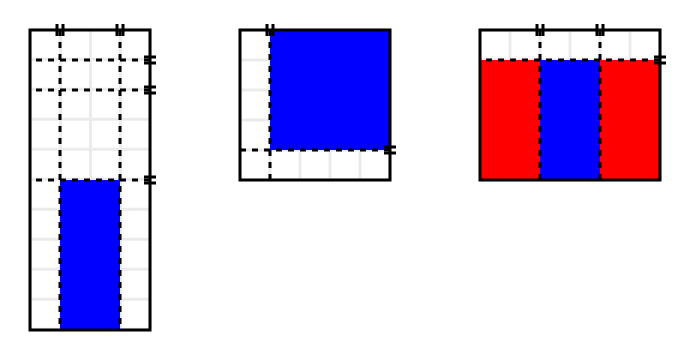
Zajo chce mať posteľ umiestnenú v bezpečí. To sú také časti územia, cez ktoré nemieri žiaden ostreľovač. Všimneme si, že priestor medzi dvomi susednými ostreľovačmi je vždy bezpečný. Podobne územie medzi nesusednými ostreľovačmi je vždy nebezpečné, lebo sa medzi nimi nachádza nejaký iný ostreľovač.

Pomalšie riešenie

Pre každú dvojicu susedných ostreľovačov zo severu, prejdeme každú dvojicu susedných ostreľovačov z východu. Šírku medzery medzi ostreľovačmi zo severu označme \(a\), šírku medzery medzi ostreľovačmi z východu označme \(b\). Časť miestnosti ohraničená týmito dvojicami je tvorená obdĺžnikom so stranami \(a\) a \(b\). Obsah tohto obdĺžnika je zrejme \(a \cdot b\). Pri prechádzaní všetkými týmito možnosťami, si počítame maximálny obsah, ktorý sme doposiaľ našli. Nakonci iba vypíšeme toto číslo. Takéto riešenie má časovú zložitosť \(O(m \cdot n)\), lebo týchto dvojíc je rádovo \(m \cdot n\) a každú spracujeme v konštantnom čase. Pretože si pamätáme celý vstup, pamäťová zložitosť je stále \(O(m+n)\).

Trik na ošetrenie okrajov

Treba si ešte dať pozor na to, že ideálne miesto pre posteľ môže byť aj pri okrajoch miestnosti. Toto treba ošetriť buď manuálne (pridať podmienky), alebo si pomôžeme trikom. Vyrobíme si dvoch ostreľovačov v každom smere takých, že budú na okrajoch miestnosti. Riešenie bude rovnako správne a rýchle, ale sprehľadníme si tým náš kód.

Všimnime si tiež, že pri všetkých premenných okrem výslednej plochy nám stačí použiť v C++ typ int, pretože podľa zadania sa nám do neho všetko zmestí. Pri výslednej ploche ale násobíme dve čísla, ktoré môžu byť veľké až \(10^6\) a vtedy by nám už int nestačil.

#include <iostream>
#include <vector>   // namiesto vectora mozeme pouzit aj obycajne pole
using namespace std;

int main() {
    int x, y, m, n;
    cin >> x >> y >> m >> n;

    // zadefinujeme vstupne polia aby sa nam tam zmestili 'okraje'
    vector<int> sever(m + 2);    // pozicie okien na severe
    vector<int> vychod(n + 2);  // pozicie okien na vychode
    // nastavime 'okraje'
    sever[0] = vychod[0] = 0;
    sever[m + 1] = x;
    vychod[m + 1] = y;

    for (int i = 1; i <= m; ++i) cin >> sever[i];
    for (int i = 1; i <= n; ++i) cin >> vychod[i];

    long long odpoved = -1;     // cast izby vacsia ako -1 sa urcite najde

    for (int sever_i = 1; sever_i < sever.size(); ++sever_i) {
        for (int vychod_i = 1; vychod_i < vychod.size(); ++vychod_i) {
        
            int dlzka_sever = sever[sever_i] - sever[sever_i - 1];
            int dlzka_vychod = vychod[vychod_i] - vychod[vychod_i - 1];
            odpoved = max(odpoved, (long long) dlzka_sever * dlzka_vychod);
            
        }
    }

    cout << odpoved << endl;

    return 0;
}

Vzorák

Na plný počet bodov bolo nutné spraviť ešte jeden myšlienkový krok. Naše pôvodné riešenie prechádzalo zbytočne veľa možnosťami. Stačilo si uvedomiť, že najväčšie územie sa vždy nachádza na prieniku území medzi dvomi najvzdialenejšími ostreľovačmi na východe a dvomi najvzdialenejšími na severe. Počítanie maximálneho územia je preto ekvivalentné s hľadaním maximálnej vzdialenosti medzi ostreľovačmi zo severu a z východu. Hľadané územie je potom rovné súčinu týchto čísel. Časová zložitosť tohto riešenia je teda \(O(m+n)\), pretože stačí raz prejsť cez obe polia. Pamäťová zložitosť je stále \(O(m+n)\), lebo si musíme pamätať vstup (tú už preto nezlepšíme).

Čerešnička na torte

Na získanie plného počtu bodov stačilo predošlé riešenie, avšak aj to sa dá ešte zlepšiť. Už nevieme zlepšiť časovú zložitosť (lebo musíme aspoň načítať vstup), vieme však zlepšiť pamäťovú zložitosť. Na vyriešenie problému totiž hľadáme maximum z nejakého počtu čísel, a to vieme robiť popri tom, ako načítavame vstup. Takéto riešenie má zložitosti \(O(m+n)\) časovú a \(O(1)\) pamäťovú.

#include <iostream>
#include <vector>   // namiesto vectora mozeme pouzit aj obycajne pole
using namespace std;

int main() {
    int x, y, m, n;
    cin >> x >> y >> m >> n;

    long long sever_max = -1;
    long long vychod_max = -1;

    // potrebujeme si pamatat predchadzajuce hodnoty, aby
    // sme vedeli zistit medzeru medzi nim a sucasnym ostrelovacom
    // na zaciatku ich nastavime na zaciatok miestnosti
    long long sever_pred = 0, vychod_pred = 0;

    // najdeme maximum na severe
    for(int i = 0; i < m; ++i) {
        long long teraz;
        cin >> teraz;
        // upravime maximum
        sever_max = max(sever_max, teraz - sever_pred);
        // cislo, ktore sme prave spracuvali, bude v dalsom prechode cyklom predchadzajuce
        sever_pred = teraz;
    }

    // najdeme maximum na vychode
    for(int i = 0; i < n; ++i) {
        long long teraz;
        cin >> teraz;
        // upravime maximum
        vychod_max = max(vychod_max, teraz - vychod_pred);
        // cislo, ktore sme prave spracuvali, bude v dalsom prechode cyklom predchadzajuce
        vychod_pred = teraz;
    }

    // musime este manualne skontrolovat druhy kraj(koniec) miestnosti
    // premenne 'sever_pred' a 'vychod_pred' obsahuju posledne nacitane cislo
    sever_max = max(sever_max, x - sever_pred);
    vychod_max = max(vychod_max, y - vychod_pred);

    // vypiseme obsah hladaneho uzemia
    cout << sever_max * vychod_max << endl;

    return 0;
}